Как вычисляется абсолютное удлинение стержня?
Из формул (2.2), (2.3) и (2.4) легко получить зависимость для абсолютного удлинения стержня:
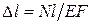 . (2.5)
. (2.5)
Выражение (2.5) иногда также называют законом Гука, но уже не для материала, а для всего стержня. Произведение 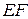 , стоящее в знаменателе формулы (2.5), характеризует жесткость стержня при растяжении (сжатии).
, стоящее в знаменателе формулы (2.5), характеризует жесткость стержня при растяжении (сжатии).
2.12. Какие напряжения возникают в наклонных сечениях стержня, то есть в сечениях, которые не являются поперечными?
Начнем ответ со следующих рассуждений. Да, мы уже умеем определять нормальные напряжения, которые возникают в опасном поперечном сечении стержня. Но можем ли мы утверждать, что эти нормальные напряжения являются наибольшими и именно их значения следует использовать для оценки прочности стержня? Нам уже известно, что касательные напряжения в поперечном сечении стержня при растяжении (сжатии) не возникают. Но возникают ли они в наклонных сечениях?
Таким образом, нам необходимо научиться определять напряжения на любых площадках, проходящих через некоторую точку К тела, и находить именно те площадки, на которых нормальные и касательные напряжения достигают наибольших значений.
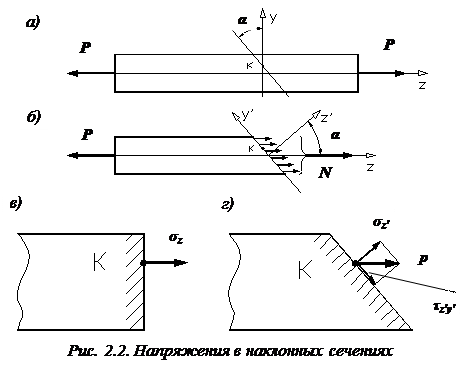
А теперь ответим на поставленный вопрос. Разрежем стержень, растягиваемый силами P, плоскостью, проходящей через точку К и наклоненной под углом 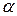 к поперечному сечению (рис. 2.2, а). Отбросим правую часть стержня.
к поперечному сечению (рис. 2.2, а). Отбросим правую часть стержня.
Внешняя нормаль 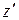 к этому наклонному сечению будет составлять с осью
к этому наклонному сечению будет составлять с осью 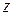 такой же угол
такой же угол 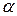 . Действие отброшенной нами правой части стержня на левую часть заменим внутренними усилиями (рис. 2.2, б). Чтобы левая часть стержня находилась в равновесии, в каждой точке наклонного сечения стержня должно возникнуть продольное противодействующее усилие. Очевидно, что равнодействующая всех этих внутренних усилий N равна внешней силе P.
. Действие отброшенной нами правой части стержня на левую часть заменим внутренними усилиями (рис. 2.2, б). Чтобы левая часть стержня находилась в равновесии, в каждой точке наклонного сечения стержня должно возникнуть продольное противодействующее усилие. Очевидно, что равнодействующая всех этих внутренних усилий N равна внешней силе P.
Будем считать, что внутренние усилия равномерно распределены по всей площади наклонного сечения 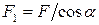 . Тогда полное напряжение в каждой точке наклонного сечения будет равно:
. Тогда полное напряжение в каждой точке наклонного сечения будет равно:
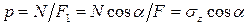 ,
,
где 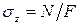 – нормальное напряжение, возникающее в этих же точках (в том числе и в точке К), но в поперечном сечении стержня (рис. 2.1, в).
– нормальное напряжение, возникающее в этих же точках (в том числе и в точке К), но в поперечном сечении стержня (рис. 2.1, в).
Разложим полное напряжение p, возникающее в некоторой точке К наклонного сечения, на две составляющие – нормальное 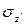 и касательное
и касательное 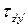 напряжения (рис. 2.2, г). Они будут равны:
напряжения (рис. 2.2, г). Они будут равны:
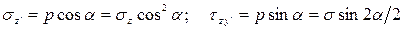 .
.
Проследим, как будет меняться каждое из этих напряжений с изменением угла наклона сечения 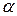 от нуля до
от нуля до 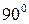 .
.
При увеличении угла 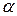 нормальное напряжение в точке К будет постепенно уменьшаться от своего максимального значения до нуля. Касательное напряжение при этом будет сначала возрастать от нулевого до максимального значения
нормальное напряжение в точке К будет постепенно уменьшаться от своего максимального значения до нуля. Касательное напряжение при этом будет сначала возрастать от нулевого до максимального значения 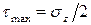 при
при 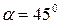 , а затем убывать. При угле
, а затем убывать. При угле 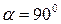 касательное напряжение снова станет равным нулю.
касательное напряжение снова станет равным нулю.
Следовательно, наибольшее нормальное напряжение действительно возникает в точках поперечного сечения стержня. В продольном сечении оно равно нулю. Отсюда следует, что продольные волокна стержня не давят друг на друга.
Наибольшие касательные напряжения возникают в сечениях, расположенных под углом 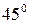 к оси стержня. В поперечном и в продольном сечениях стержня они равны нулю.
к оси стержня. В поперечном и в продольном сечениях стержня они равны нулю.
