Решение задачи Коши с помощью прямого и обратного преобразований Лапласа с нулевыми начальными условиями при пуске ненагруженной ЭМС

Система дифференциальных уравнений в каноническом виде:

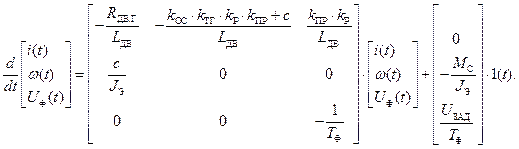
Применяя прямое преобразование Лапласа при нулевых начальных условиях, получаем систему линейных алгебраических уравнений (СЛАУ):

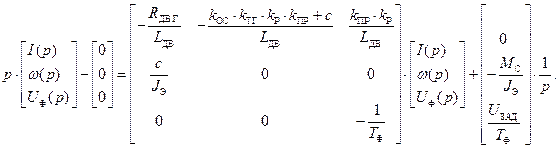
Представим СЛАУ в виде А(р)х(р)=В(р):

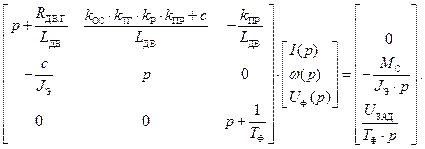
Решим СЛАУ методом обратной матрицы в программе MathCAD:

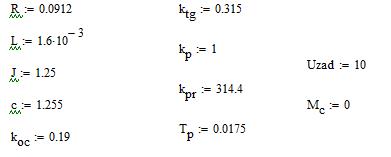
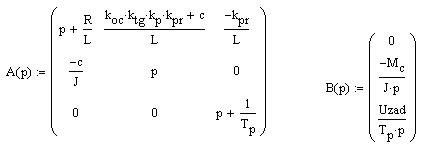
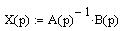
Изображения функций:

Применяя обратное преобразование Лапласа, найдем оригиналы функций, описывающих переходный процесс пуска ненагруженной ЭМС, и построим их графики:

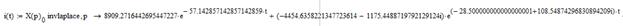
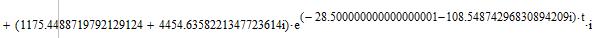
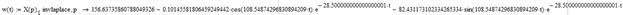
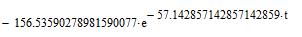
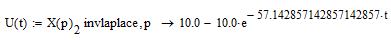
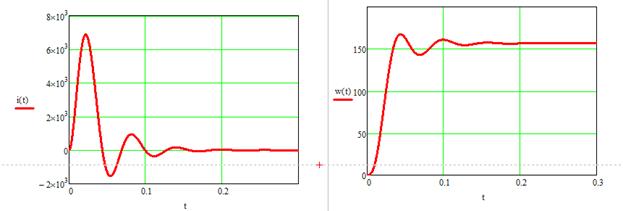
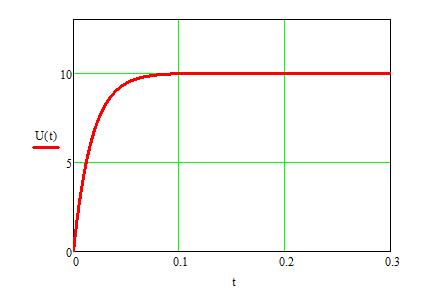
Рисунок 16 – Переходные процессы, найденные операторным методом при нулевых начальных условиях

Зависимости переменных ЭМС, определенные с помощью преобразований Лапласа, полностью совпали с моделированием в среде MATLAB Simulink и классическим методом.

Решение задачи Коши с помощью преобразований Лапласа с ненулевыми начальными условиями при реверсе ненагруженной ЭМС

Система дифференциальных уравнений в каноническом виде:

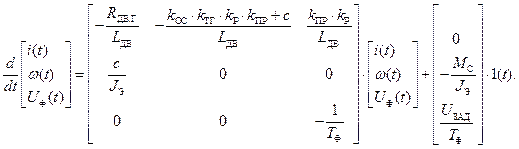
В качестве ненулевых начальных условий в случае реверса ненагруженной ЭМС считаем: ; ;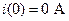

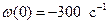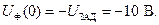
Применяя к системе дифференциальных уравнений прямое преобразование Лапласа, получаем СЛАУ:

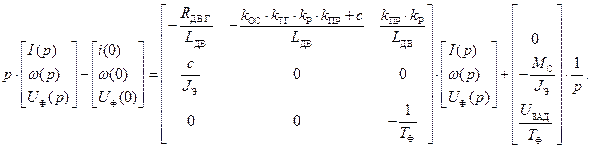
Представим СЛАУ в виде А(р)х(р)=В(р):

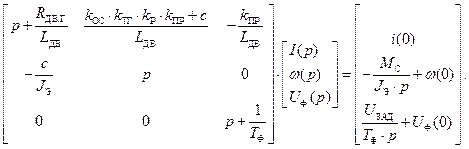
Решим СЛАУ методом обратной матрицы в программе MathCAD:

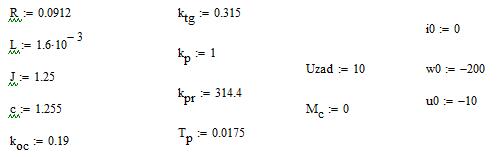
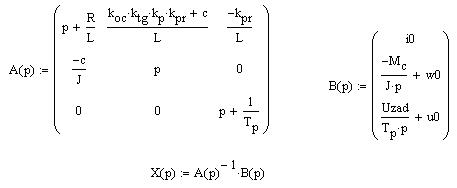
Изображения функций при реверсе ненагруженной ЭМС:

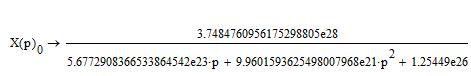
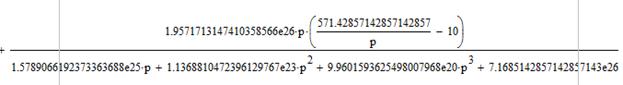
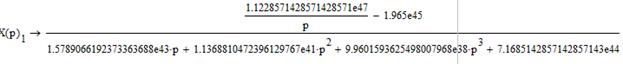
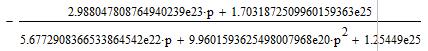
Применяя обратное преобразование Лапласа, найдем оригиналы функций, описывающих переходный процесс реверса ненагруженной ЭМС, и построим их графики:

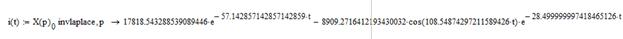
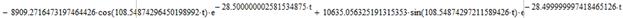
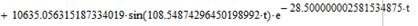
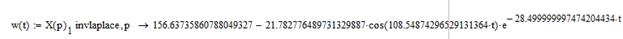
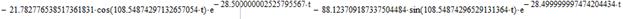
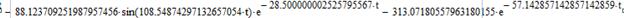
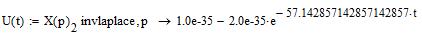
Применяя обратное преобразование Лапласа, найдем оригиналы функций, описывающих переходный процесс реверса ненагруженной ЭМС, и построим их графики:

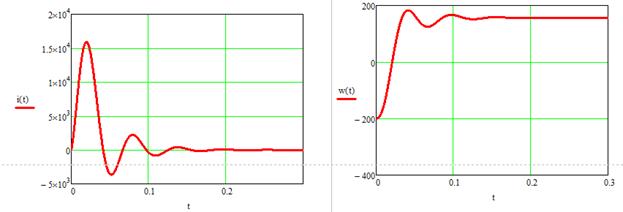
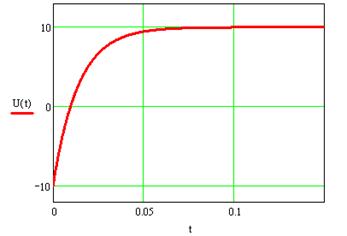
Рисунок 17 – Переходные процессы при реверсе ЭМС, найденные операторным методом

Решение задачи Коши для пуска ненагруженной ЭМС с помощью определителя Вандермонда

Задаем параметры ненагруженной ЭМС в программной среде MathCAD:

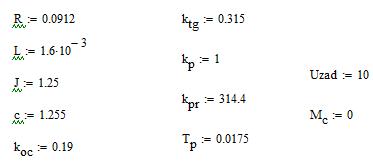
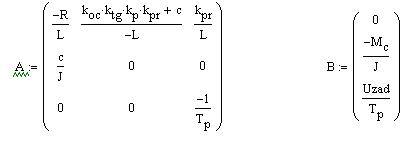
Находим собственные значения матрицы коэффициентов А:

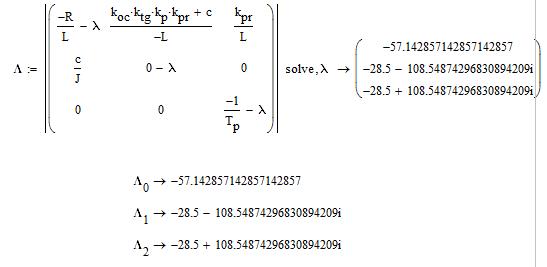
Полный и частные определители Вандермонда:

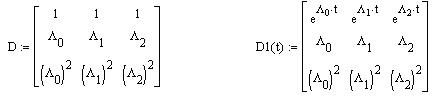
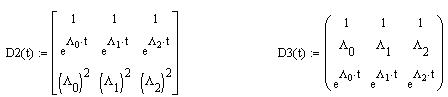
Матричная функция F(t) и временные характеристики:

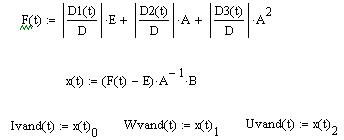
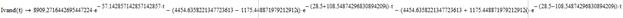
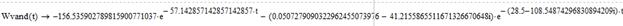
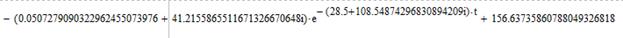
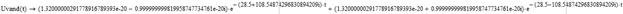
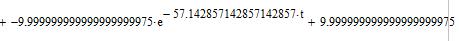
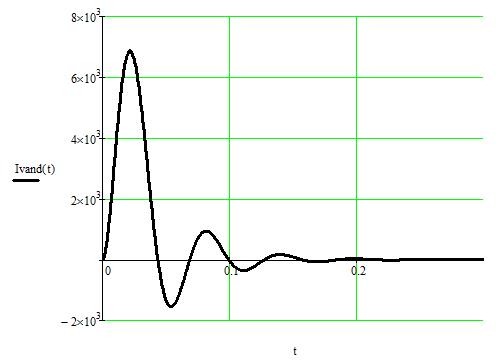
Рисунок 18 – Зависимость i(t), найденная с помощью определителя Вандермонда

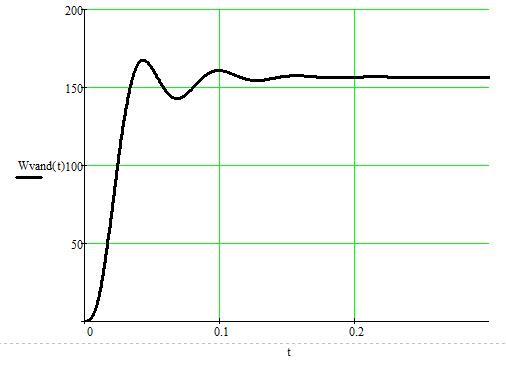
Рисунок 19 – Зависимость 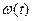, найденная с помощью определителя Вандермонда

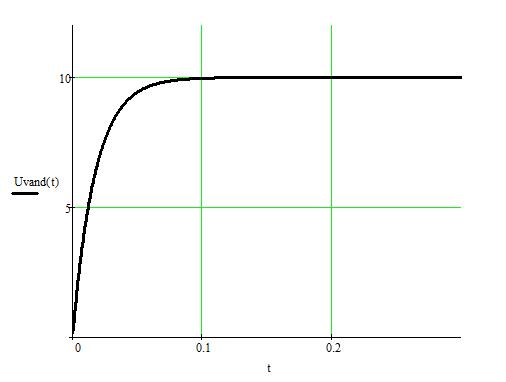
Рисунок 20 – Зависимость 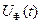, найденная с помощью определителя Вандермонда

Результаты, полученные с помощью метода определителей Вандермонда, полностью повторяют аналогичные данные, найденные классическим и операторным методами, а также моделирование в MATLAB.