Азбука теории графов. Маршрут, путь, простой путь. Цикл. Простой цикл. Связность в графе

Определение. Маршрутом 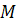в графе 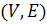называется последовательность вершин 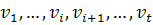, где пара соседних вершин 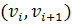является ребром графа.

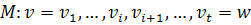
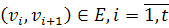-1

В этом случае будем говорить, что маршрут M соединяет вершины .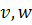

Пример.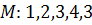

Определение. Путем, соединяющим пару вершин 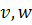будем называть маршрут, соединяющий данную пару вершин и не содержащий повторяющихся ребер.

Определение. Простым путем, соединяющим пару вершин 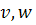будем называть путь, соединяющий данную пару и не содержащий повторяющихся вершин.

Определение. Пару вершин 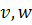в графе 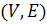будем называть связной, если либо вершины совпадают, либо существует маршрут, соединяющий две эти вершины.

Пример.Любая пара вершин в следующем графе связана:

В следующем графе связанными являются не все вершины:

Вершины 1 и 2 связаны, а, например, вершины 2 и 3 не связаны.

Утверждение. Если в графе существует маршрут, соединяющий пару вершин, то существует простой путь, который соединяет данную пару вершин.

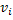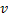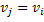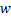Рассмотрим маршрут, соединяющий вершины 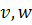. Предположим, что вершина 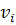повторяется на маршруте. Тогда вырежем участок маршрута 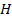между повторяющимися вершинами и соединим полученные части. Данную операцию будем повторять до тех пор, пока в маршруте не будет повторяющихся вершин.

Таким образом, получен простой путь, соединяющий пару вершин 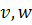. Поэтому для связности вершин достаточно наличие простого пути, который их соединяет.

Определение. Циклом называется путь, в котором начальная и конечная врешины совпадают.

Пример.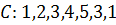

Определение. Простым циклом называется путь, в котором вершины не повторяются, за исключением первой и последней. Другими словами, простой цикл - это цикл без самопересечения.

Пример. Простой цикл: .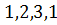

Связные графы

Отношение связности между вершинами в графе обладает тремя свойствами:

1. Рефлексивность (отражение).

Любая вершина связана сама с собой.

2. Симметричность.

Если вершина 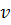связана с вершиной 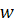, то верно и обратное: вершина 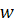связана с вершиной .

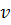3. Транзитивность.

Если вершина 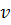связана с вершиной 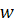, а вершина 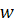связана с вершиной 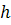, то вершина 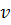связана с вершиной .

…

…

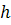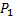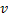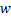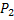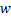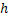Путь, который связывает 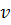и 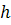, можно получить соединением путе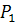й и .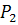

Отношение связности разбивает все вершины графа на компоненты связанности:

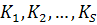
Любая пара вершин, входящая в одну компоненту связности связана. Любые вершины из разных компонент связности между собой не связаны.

Пример. Представленный граф состоит из двух компонент связности. В первой компоненте находятся вершины 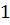и 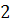, а вторая компонента включает в себя вершину .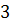