Задание (Транспортная задача)

Имеются 3 пункта поставки однородного груза А1, А 2 , А 3 и 5 пунктов по- требления этого груза В 1 , В 2 , В 3 , В 4 , В 5 . На пунктах А I ( I = 1,2,3 ) груз находится соответственно в количествах а1, а 2 , а 3 условных единиц. В пункты В J ( J= 1,2,3,4,5 ) требуется доставить соответственно b J единиц груза. Стоимость пере- возки единицы груза (с учетом расстояний) из А I в В J определена матрицей С={c ij

}. Решить задачу тремя методами (северо-западного угла, минимальной стоимости и методом Фогеля) и найти такой план закрепления потребителей и поставщиков, чтобы общие затраты на перевозки были минимальны.

1). а1= 200, а 2 =170, а 3 = 180,

b1= 100, b 2 = 70, b 3 = 180,

b 4 = 150, b 5 = 50

2). а1= 120, а 2 = 250, а 3 = 150,

b1= 90, b 2 = 70, b 3 = 160,

ç

ø

b 4 = 130, b 5 = 70

æ 7 ç				3 ö ÷	æ10 ç				3 ö ÷
С= ç 5				2 ÷	С= ç 9				7 ÷

ç

ø

è10 3 5

8 12÷

è11 5

7 13

12÷

3). а1= 280, а 2 =350, а 3 = 250,

b1=130, b 2 =100, b 3 = 300,

b 4 = 270, b 5 = 80

4). а1= 250, а 2 = 270, а 3 = 150,

b1= 100, b 2 = 170, b 3 = 160,

b 4 = 170, b 5 = 70

æ13 ç				6ö ÷	æ 5 ç				16ö ÷
С= ç12				8÷	С= ç 8				18 ÷

ç

è14

7 10 14 ÷

è10

11 13 7

20÷

ç

ø

ø

5). а1= 230, а 2 =250, а 3 = 200,

b1=100, b 2 =180, b 3 = 160,

b 4 = 160, b 5 = 80

6). а1= 100, а 2 = 140, а 3 = 150,

b1= 60, b 2 = 50, b 3 = 80,

b 4 = 160, b 5 = 40

æ 6 ç				4 ö ÷	æ10 ç				8ö ÷
С= ç12				3 ÷	С= ç 9				7÷

ç

è 9 5 17

14 10÷

è 9 6

5 3 ø

ø

ç

÷

7). а1= 175, а 2 =150, а 3 = 125,

b1= 105, b 2 = 75, b 3 = 50,

b 4 = 145, b 5 = 75

8). а1= 200, а 2 = 250, а 3 = 160,

b1= 120, b 2 = 120, b 3 = 100,

b 4 = 210, b 5 = 60

æ10 ç				6 ö ÷	æ10 ç				20ö ÷
С= ç12				6 ÷	С= ç 21				7 ÷

ç

è11 5 6

7 10÷

è12

15 16 13

21÷

ø

ç

ø

9). а1=390, а 2 = 450, а 3 = 400,

b1=310, b 2 =250, b 3 = 150,

ø

b 4 = 440, b 5 = 90

10). а1= 300, а 2 = 360, а 3 = 400,

b1= 150, b 2 = 350, b 3 = 300,

ç

ø

b 4 = 150, b 5 = 110

æ 20 ç				12ö ÷	æ 9 ç				3 ö ÷
С= ç 25				10 ÷	С= ç 8				2 ÷

ç

è 24

7 10 13

22÷

è10

7 11 15

20÷

11). а1=270, а 2 = 390, а 3 = 290,

b1=150, b 2 =100, b 3 = 250,

b 4 = 340, b 5 = 110

12). а1= 380, а 2 = 450, а 3 = 420,

b1= 230, b 2 = 200, b 3 = 400,

b 4 = 270, b 5 = 230

æ ç					6 ö ÷	æ15 ç				10ö ÷
С= ç17					7 ÷	С= ç14				7 ÷

ç

è 20

9 15 7

25÷

è16

8 10

12 17 ÷

ø

ç

ø

13). а1=150, а 2 = 230, а 3 = 250,

b1=110, b 2 =100, b 3 = 200,

b 4 = 140, b 5 = 80,

14). а1= 250, а 2 = 190, а 3 = 200,

b1= 180, b 2 = 100, b 3 = 130,

b 4 = 140, b 5 = 90

æ 8 ç				5ö ÷	æ 8 ç				4ö ÷
С= ç 7				4÷	С= ç 3				6÷

ç

ø

è 8 7 5 6 ÷

è 2 9

6 5 ø

ç

÷

15). а1=180, а 2 = 210, а 3 = 190,

b1=100, b 2 =150, b 3 = 130,

b 4 = 120, b 5 = 80

16). а1= 310, а 2 = 250, а 3 = 240,

b1= 290, b 2 = 110, b 3 = 170,

b 4 = 130, b 5 = 100

æ 6 ç				2ö ÷	æ 7 ç				3ö ÷
С= ç 5				8 ÷	С= ç 4				7 ÷

ç

è 4 7

3 5 ø

è 6 4 9 5 ÷

ç

÷

ø

17). а1=280, а 2 = 200, а 3 = 220,

b1=110, b 2 =100, b 3 = 220,

b 4 = 180, b 5 = 90

18). а1= 170, а 2 = 230, а 3 = 180,

b1= 95, b 2 = 130, b 3 = 120,

ç

ø

b 4 = 155, b 5 = 80

æ10 ç				6 ö ÷	æ10 ç				5 ö ÷
С= ç 7				10÷	С= ç 9				13÷

ç

ø

è 9 8 3 7 ÷

è 8 5 7 6 ÷

19). а1=260, а 2 = 190, а 3 = 120,

b1=100, b 2 = 120, b 3 = 200

b 4 = 80, b 5 = 70

20). а1= 330, а 2 = 300, а 3 = 270,

b1= 120, b 2 = 200, b 3 = 310,

b 4 = 190, b 5 = 80

æ11 ç				4 ö ÷	æ12 ç				8ö ÷
С= ç10				12÷	С= ç 3				6÷

ç

ø

è 9 6 5 7 ÷

è 7 14 10 11 ÷

ç

ø

21). а1=280, а 2 = 170, а 3 = 260,

b1=160, b 2 =140, b 3 = 200,

b 4 = 100, b 5 = 110

22). а1= 300, а 2 = 260, а 3 = 230,

b1= 140, b 2 = 250, b 3 = 150,

b 4 = 160, b 5 = 90

æ 5 ç				8 ö ÷	æ 9 ç				5ö ÷
С= ç 7				8 ÷	С= ç 5				6÷

ç

ø

è 5 11 12 10 ÷

è 7 13 5 6 ø

ç

÷

23). а1= 200, а 2 = 150, а 3 = 50,

b1= 60, b 2 = 70, b 3 = 80,

b 4 = 90, b 5 = 100

24). а1= 200, а 2 = 130, а 3 = 250,

b1= 90, b 2 = 100, b 3 = 160,

b 4 = 150, b 5 = 80

æ 6 ç				8 ö ÷	æ 9 ç				5ö ÷
С= ç 1				10÷	С= ç13				6÷

ç

ø

è 3 4 4 7 ÷

è 6 7 10 5 ÷

ç

ø

25). а1=200, а 2 = 260, а 3 = 240,

b1=120, b 2 =180, b 3 = 210,

b 4 = 90, b 5 = 100,

26) а1= 200, а 2 = 170, а 3 = 180,

b1= 100, b 2 = 70, b 3 = 180,

ç

ø

b 4 = 150, b 5 = 50

æ 6 ç				4ö ÷	æ 7 ç				3 ö ÷
С= ç10				3÷	С= ç 5				2 ÷

ç

ø

è 8 13 11 7 ÷

è10 3 5

8 12÷

27). а1=250, а 2 = 190, а 3 = 200, b

1 = 180, b 2 = 100,

b 3 = 130, b 4 = 140, b 5 = 90

28). а1= 200, а 2 = 250, а 3 = 160, b1=

120, b 2 = 120, b 3 = 100, b 4 = 210, b 5 =

ç

è 2 9

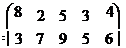
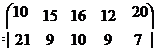
6 5 ø

è12

15 16 13

21÷

ç

ø

÷

29). а1=230, а 2 = 250, а 3 = 200,

b1 = 100, b 2 = 180,

b 3 = 160, b 4 = 160, b 5 = 80

30) 1 = 270, а 2 = 390, а 3 = 290,

b1= 150, b 2 = 100, b 3 = 250,

b 4 = 340, b 5 = 110

ç

è 9 5 17

ø

14 10÷

ç

ç

æ 6 ç 4 ö ÷ æ 6 ö С= ç12 3 ÷ С= ç17   7 ÷

è 20

9 15 7

÷

ø

25÷

Задание 3.

Дана целевая функция и нелинейная система ограничений. Графическим мето- дом найти глобальные экстремумы (максимум и минимум) задачи.

№ Вар.	Задача	№ Вар.	Задача
	z = 2x1+ x2(max, min) ì(x - 2)2+ (x - 1)2³ 4, 1 2 ï í(x - 2)2+ (x - 1)2£ 9, 1 2 ïx + x ³ 3; î 1 2 x1³ 0; x2³ 0.		z = x1 + x2(max, min) ìïx 2 + x 2 ³ 9, 1 2 í ïî(x - 3)2 + (x - 3)2 £ 4; 1 2 x1³ 0; x2³ 0.
	z = x1- x2(max, min) ïìx 2 + x 2 £ 9, 1 2 í ïî(x - 3)2 + (x - 3)2 £ 4; 1 2 x1³ 0; x2³ 0.		z = x1 - x2(max, min) ìï(x - 1)2 + (x -1)2 ³ 1, 1 2 í 2 2 ïî(x1 - 3) + (x2 - 3) £ 9; x1³ 0; x2³ 0.

	z = x1 + x2(max, min) ìx1x2³ 1, í 2 2 îx1 + x2 £ 9; x1³ 0; x2³ 0.		z = x1- x2(max, min) ì(x1- 2)+ (x2+ 1)³ 4, í îx1 + x2£ 6; x1³ 0; x2³ 0.
	z = 4x1+ x2(max, min) ì(x - 2)2+ (x - 1)2³ 4, 1 2 ï í(x - 2)2+ (x - 1)2£ 9, 1 2 ïx + x £ 5; î 1 2 x1³ 0; x2³ 0.		z = 2x1- x2(max, min) ì(x1- 2)(x2+ 1)³ 4, í îx1 + x2£ 6; x1³ 0; x2³ 0.
	z = x1 - 2x2(max, min) ìx1x2³ 1, ï ï 11 í(x1 - 4)(x2- 4) ³ , ï 3 ïîx1 £ 4; x1³ 0; x2³ 0.		z = x1 - 2x2(max, min) ìx1x2£ 1, ï ï 11 í(x1 - 4)(x2- 4) ³ ï 3 ïîx1 £ 4; x1³ 0; x2³ 0.
	z = 2x1+ x2(max, min) ì(x - 2)2+ (x - 1)2³ 4, 1 2 ï í(x - 2)2+ (x - 1)2£ 9, 1 2 ïx + x £ 3; î 1 2 x1³ 0; x2³ 0.		z = x1 - x2(max, min) ìïx 2 + x 2 ³ 9, 1 2 í ïî(x - 3)2 + (x - 3)2 £ 4; 1 2 x1³ 0; x2³ 0.
	z = x1 + x2(max, min) ïìx 2 + x 2 £ 9, 1 2 í ïî(x - 3)2 + (x - 3)2 £ 4; 1 2 x1³ 0; x2³ 0.		z = x1 + x2(max, min) ìï(x - 2)2 + (x - 1)2 ³ 1, 1 2 í ïî(x - 3)2 + (x - 3)2 £ 9; 1 2 x1³ 0; x2³ 0.
	z = x1 + x2(max, min) ìx1x2³ 1, í 2 2 îx1 + x2 £ 9; x1³ 0; x2³ 0.		z = x1+ x2(max, min) ì(x1- 2)(x2+ 1)£ 4, í îx1 + x2£ 6; x1³ 0; x2³ 0.
	z = x1- 4x2(max, min) ì(x - 2)2+ (x - 1)2³ 4, 1 2 ï í(x - 2)2+ (x - 1)2£ 9, 1 2 ï(x + x £ 5; î 1 2 x1³ 0; x2³ 0.		z = x1+ 2x2(max, min) ì(x1- 2)(x2+ 1)³ 4, í îx1 + x2£ 6; x1³ 0; x2³ 0.

	z = x1+ x2(max, min) ìx1x2³ 1, ï ï 11 í(x1- 4)(x2- 4) £ , ï 3 ïîx1 £ 4 x1³ 0; x2³ 0.		z = x1+ x2(max, min) ìx1x2£ 1, ï ï 11 í(x1- 4)(x2- 4) ³ , ï 3 ïîx1 £ 4 x1³ 0; x2³ 0.
	z = x1 - 2x2(max, min) ìx 2 + x 2 £ 16, ï 1 2 í3x1- x2³ 0, ïx - 3x £ 0; î 1 2 x1³ 0; x2³ 0.		z = x1 + x2(max, min) ïì(x - 1)2 + (x -1)2 ³ 9, 1 2 íï x - 4)2 + (x - 4)2 £ 4; î(1 2 x1³ 0; x2³ 0.
	z = x1 - x2(max, min) ìï(x - 1)2 + (x -1)2 £ 9, 1 2 í ïî(x - 4)2 + (x - 4)2 £ 4; 1 2 x1³ 0; x2³ 0.		z = x1 + x2(max, min) ìï(x -1)2 + (x - 1)2 ³ 9, 1 2 í ïî(x - 4)2 + (x - 4)2 £ 4; 1 2 x1³ 0; x2³ 0.
	z = x1+ x2(max, min) ì(x1- 1)(x2 - 1)³ 1 í î(x - 1)2+ (x - 1)2£ 9 1 2 x1³ 0; x2³ 0		z = x1- x2(max, min) ì(x1 - 3)× x2£ 4 íx + x £ 8 î 1 2 x1³ 0; x2³ 0
	z = 4x1 + x2(max, min) ì(x - 1)2+ x 2 ³ 4 1 2 ï 2 í(x - 1) + x 2 £ 9 1 2 ï ïîx1 + x2 £ 3 x1³ 0; x2³ 0		z = 2x1- x2(max, min) ì(x1- 1)(x2 + 1)³ 4 í îx1 + x2 £ 5 x1³ 0; x2³ 0
	z = x1 - 2x2(max, min) ì(x1 - 1)(x2 - 1)³ 1 ï 11 ï í(x1 - 5)(x2- 5) ³ ï 3 ïîx1 £ 5 x1³ 0; x2³ 0		z = x1- 3x2(max, min) ìx 2 + x 2 £ 9 1 2 ï í2x1- x2³ 0 ï îx1- 2x2³ 0 x1³ 0; x2³ 0

Задание 4

Для задачи с нелинейной целевой функцией и линейной системой ограничений графическим методом найти максимум и минимум.

№ варианта Задача № варианта Задача z = x1 - 2x2(max, min) x1+ x2 ìx2+ x1³ 6 ï í2x2- x1£ 6 ïx - 2x + 6 ³ 0 î 2 1 x1³ 0; x2³ 0 z = x1+ x2 (max, min) 2x1 - x2 ìx2+ x1³ 4 ï í3x2- 2x1£ 7 ïx - 4x + 11 ³ 0 î 2 1 x1³ 0; x2³ 0 z = 2x1- x2(max, min) x1 - x2 ì2x2+ 3x1 ³ 11 ï íx2£ 4 ïx - 3x + 8 ³ 0 î 2 1 x1³ 0; x2³ 0 z = 2x1 (max, min) x1- 3x2 ìx2+ x1³ 5 ï í3x2+ 2x1£ 13 ïx ³ 1 î 2 x1³ 0; x2³ 0 z = (x - 6)2+ (x - 6)2(max, min 1 2 ìx2+ x1 - 7 ³ 0 ï í3x2+ 2x1£ 18 ïx ³ 2 î 2 x1³ 0; x2³ 0 ) 6 z = (x - 6)2+ (x - 5)2(max, min 1 2 ìx2- x1 - 2 £ 0 ï í3x2+ 2x1 - 16 ³ 0 ï2x + 3x - 19 £ 0 î 2 1 x1³ 0; x2³ 0

)

	z = x1+ x2 (max, min) 2x2- x1 ìx2+ x1³ 6 ï í3x2- 2x1£ 8 ïx - 4x + 14 ³ 0 î 2 1 x1³ 0; x2³ 0		z = 2x1 - x2(max, min) x1 - x2 ì2x2+ 3x1 - 16³ 0 ï íx2£ 5 ïx - 3x + 10 ³ 0 î 2 1 x1³ 0; x2³ 0
	z = 2x2 (max, min) x2- 3x1 ìx2+ x1 - 7 ³ 0 ï í3x2+ 2x1£ 18 ïx ³ 2 î 2 x1³ 0; x2³ 0		z = x2+ 3x1 (max, min) x1 + x2 ìx2- x1 - 2 £ 0 ï í3x2+ 2x1- 16 ³ 0 ï2x + 3x £ 19 î 2 1 x1³ 0; x2³ 0

	z = (x - 1)2+ (x - 1)2 (max, min) 1 2 ìx2+ x1³ 6 ï í2x2- x1£ 6 ïx - 2x + 6 ³ 0 î 2 1 x1³ 0; x2³ 0		z = (x + 1)2+ (x - 1)2 (max, min) 1 2 ìx2+ x1³ 4 ï í3x2- 2x1£ 7 ïx - 4x + 11 ³ 0 î 2 1 x1³ 0; x2³ 0
	z = x 2 + (x - 1)2(max, min) 1 2 ì2x2+ 3x1³ 1 ï íx2£ 4 ïx - 3x + 8 ³ 0 î 2 1 x1³ 0; x2³ 0		z = (x - 4)2+ (x - 5)2(max, min) 1 2 ìx2+ x1³ 5 ï í3x2+ 2x1£ 13 ïx ³ 1 î 2 x1³ 0; x2³ 0
	z = (x - 2)2+ (x - 3)2(max, min) 1 2 ìx2£ x1 + 2 ï í3x2³ -2x1 + 11 ï2x + 3x £ 14 î 2 1 x1³ 0; x2³ 0		z = (x - 5)2+ (x - 5)2(max, min) 1 2 ìx2+ x1³ 8 ï í2x2- x1£ 7 ïx - 2x + 7 ³ 0 î 2 1 x1³ 0; x2³ 0
	z = (x - 3)2+ (x - 4)2(max, min) 1 2 ìx2+ x1³ 6 ï í3x2- 2x1£ 8 ïx - 4x + 14 ³ 0 î 2 1 x1³ 0; x2³ 0		z = (x + 1)2+ (x + 7)2(max, min) 1 2 ì2x2+ 3x1 - 16³ 0 ï íx2£ 5 ïx - 3x + 10 ³ 0 î 2 1 x1³ 0; x2³ 0
	z = (x - 6)2+ (x - 6)2(max, min) 1 2 ìx2+ x1 - 7 ³ 0 ï í3x2+ 2x1£ 18 ïx ³ 2 î 2 x1³ 0; x2³ 0		z = (x - 6)2+ (x - 5)2(max, min) 1 2 ìx2- x1 - 2 £ 0 ï í3x2+ 2x1 - 16 ³ 0 ï2x + 3x - 19 £ 0 î 2 1 x1³ 0; x2³ 0
	z = x1 - 2x2(max, min) x1+ x2 ìx2+ x1 - 4 ³ 0 ï í2x2- x1- 5 £ 0 ïx - 2x + 5 ³ 0 î 2 1 x1³ 0; x2³ 0		z = x1+ x2 (max, min) 2x1 - x2 ìx2+ x1- 5 ³ 0 ï í4x2- x1£ 15 ïx - 4x + 15 ³ 0 î 2 1 x1³ 0; x2³ 0

	z = 2x1- x2(max, min) x1 - x2 ì2x2+ 3x1 - 14³ 0 ï í3x2+ x1£ 14 ïx - 2x + 7 ³ 0 î 2 1 x1³ 0; x2³ 0		z = 2x1 (max, min) x1- 3x2 ì4x2+ 3x1 - 19³ 0 ï íx2- 4 £ 0 ïx - 3x + 14 ³ 0 î 2 1 x1³ 0; x2³ 0
	z = x1+ 3x2(max, min) x1+ x2 ì2x2£ 3x1 ï íx2+ 4x1³ 11 ï3x + x £ 22 î 2 1 x1³ 0; x2³ 0		z = (x - 2)2+ (x - 3)2(max, min) 1 2 ìx2+ x1 - 4 ³ 0 ï2x - x - 5 £ 0 í 2 1 ïx - 2x + 5 ³ 0 î 2 1 x1³ 0; x2³ 0
	z = (x - 4)2+ (x - 2)2(max, min) 1 2 ìx2+ x1 - 5 ³ 0 ï í4x2- x1£ 15 ïx - 4x + 15 ³ 0 î 2 1 x1³ 0; x2³ 0		z = (x - 3)2+ (x - 2)2(max, min) 1 2 ì2x2+ 3x1- 14³ 0 ï í3x2+ x1£ 14 ïx - 2x + 7 ³ 0 î 2 1 x1³ 0; x2³ 0
	z = (x + 1)2+ (x - 4)2(max, min) 1 2 ì4x2+ 3x1- 19³ 0 ï íx2- 4 £ 0 ïx - 3x + 14 ³ 0 î 2 1 x1³ 0; x2³ 0		z = (x + 1)2+ x 2 (max, min) 1 2 ì2x2£ 3x1 ï íx2+ 4x1³ 11 ï3x + x £ 22 î 2 1 x1³ 0; x2³ 0

Задание 5.

Найти точки условного экстремума функции U при заданных ограничениях ме- тодом Лагранжа.

№ варианта	Задача
	U = x2+ y 2 - xy + x + y - 4, ïðè x + y + 3 = 0.
	ì y + 2z= 3, U = 2xz - yz, ïðè í îx + y = 2.
	U = 2x + y, ïðè x2+ y 2 = 1.

	ìx+ y = 2, U = xy + yz, ïðè í î y + z = 2.
	U = 2xy, ïðè 2x - 3y - 4 = 0.
	ìx- y = 2, U = xy + yz, ïðè í î y + z = 4.
	U = 2x + y - 2z, ïðè x2- y 2 + z 2 = 36.
	U = 1 + 1 , ïðè x + y = 2. x y
	ì y + z = 6, U = 4x3+ y 2 - z 2 + 9xy, ïðè í îx + y = 2.
	U = 6 - 4x - 3y, ïðè x2+ y 2 = 1.
	ìx+ y = 2, U = 4 y3+ x2- z 2 + 9xy, ïðè í îx + z = 6.
	U = 2x + y, ïðè x2+ y 2 = 1.
	ìx+ z = 6, U = 4 y3+ z 2 - x2+ 9 yz, ïðè í îx + z = 2.
	U = 4x + 9y - 25, ïðè 4x2+ 36y 2 = 9.
	ì2x+ y + z = 8, U = 4 y3+ x2- z 2 + 9xy, ïðè í î3x + y + 2z = 14.
	U = x + y , ïðè x2 + y 2 = 1. 2 3
	ì2x+ 3y+ z = 14, U = 4z 3 + y 2 - x2 + 9 yz, ïðè í îx + y = 6.
	U = 3x2- 8xy + 7 y 2 , ïðè x2+ y2-1 = 0.
	ì2x+ y - z = -2, U = 4x3+ y 2 - z 2 + 9xy, ïðè í îx + 2 y + z = 8.
	U = x2+12xy + 2y 2 , ïðè 4x2+ y 2 - 25 = 0.
	ì2x+ y + z = 8, U = 4 y3+ x2- z 2 + 9xy, ïðè í îz - y = 4.
	U = 2x - y + z, ïðè x2+ y2+ z 2 = 1.

	ì2x+ 3y+ z = 14, U = 4z 3 + y 2 - x2 + 9 yz, ïðè í îx - y - 2z = 2.
	U = x2+ y 2 , ïðè 3x + 2y -11 = 0
	ìx+ y + 2z= 8, U = 4 y3+ z 2 - x2+ 9 yz, ïðè í îx - y = 4.
	U = -xy 2 , ïðè x + 2y -1 = 0
	ìx+ 2 y + z = 8, U = 4x3+ y 2 - z 2 + 9 yz, ïðè í îx + 3y + 2z = 14.
	U = xy 2 z 2 , ïðè x + 2y + 3z = 12 (xñ0, yñ0, zñ0).
	ì2x+ y + 3z= 14, U = 4 y3+ z 2 - z 2 + 9 yz, ïðè í îx + z = 6.
	U = x + y - 2 2, ïðè x2+ y 2 = 1. 2 2

V. ЛЕКЦИОННЫЙ МАТЕРИАЛ.

Линейное программирование.

Симплексный метод

Пусть требуется найти max Z,

n

Z = åc j x j , (1)

j = 1

при условиях:

ìx1

ï

ïx2

í

+ a1m+1 xm+1

+ a 2m+1 xm+1

+ ... + a1nxn

+ ... + a 2nxn

= b1,

= b2,

(2)

ï. . . . . . . . . . . . . . . . . .

îïx m

+ a mm+1 xm+1

+ ... + a mnxn

= bm ,

xj ³ 0 (j=1..n),

где aij, cj bi - постоянные числа (bi > 0 , m < n ).

Введя векторы:

æ 1ö

æ 0ö

æ 0ö

æ a1m+1 ö

æ a1nö

æ b1 ö

ç 0÷

ç 1÷

ç 0÷

ç a ÷

ç a ÷

ç b ÷

A1= ç

÷ ,A2= ç

÷ ,...,Am= ç

÷ , Am+1=

ç 2m+1 ÷ ,...,An= ç

2n ÷ ,A0= ç

2 ÷ ,

ç...÷

ç...÷

ç...÷

ç ... ÷

ç ... ÷

ç ... ÷

ç ÷ ç ÷ ç ÷

ç ÷ ç ÷ ç ÷

è 0ø

è 0ø

è 1ø

èamm+1 ø

èamnø

è bmø

можно записать систему (2) в векторной форме :

x1 A1+ x2A2+ ... xm Am + xm+1Am+1+ ... + xn An= A0. (3)

Нетрудно заметить. что справедливо равенство: b1A1 + b2A2+ ... +bmAm = A0,

а это означает, что X0= (b1,b2,...,bm,0,..,0) является решением системы (2) или

начальным опорным планом задачи. Этот план определяется системой базисных векторов A1,A2,...,Am m-мерного пространства. Каждый вектор Aj может быть

представлен в виде линейной комбинации векторов этого базиса: Aj=

(j=0..n).

m

åxij Ai

i = 1

Положим Zj= Cб Aj=

m

åci xij

i = 1

, где Cб = (c1, c2, ...,cm) - ценовoй вектор базиса и

Dj = Zj- cj (xij- компоненты вектора Aj в данном базисе).

Оптимальность опорного плана и последующие шаги решения задачи опре- деляются следующими теоремами:

Теорема 1.Опорный план X=(x1, x2,..,xm,0,...,0) задачи линейного програм- мирования (1)-(2) является оптимальным, если Dj³0 для всех j (j=1,...,n).

Теорема 2. Если для некоторого j=k Dj<0 и среди чисел aik (i=1,..,m) нет по- ложительных чисел, то целевая функция задачи не ограничена на множестве ее планов.

Теорема 3.Если опорный план X задачи не вырожден и Dk < 0, но среди чи- сел aik есть положительные (не все aik£ 0 ), то существует опорный план X1такой, что Z(X1)>Z(X).

Исходные данные и процесс вычисления (переход к новому опорному плану) удобно записывать в табл. 1

Таблица 1

i	базис	Сб	A0	c1	c2	...	ck	...	cn
A1	A2	...	Ak	...	An
	E1	C10	b10	a11	a12	...	a1k	...	a1n
	E2	C20	b20	a21	a22	...	a2k	...	a2n
...	...	...	...	...	...	...	...	...	...
m	Em	Cm0	bm0	am1	am2	...	amk	...	amn
m+1			Z0	D1	D2	...	Dk	... D	n

Базисный вектор Ei(i=1,...,m) совпадает с As, если ais = 1, а все остальные компоненты равны нулю. Соответствующий коэффициент csпри xs целевой функ- ции записан в Cб. Значения Dj=Zj-cj=AjCб-cj(j=0,...,n) записаны в (m + 1)-й строке. В столбце A0 записаны свободные члены biсистемы (8) в порядке, соответствующем каждому базисному вектору. Компоненты вектора A0и составляют опорный план (bi>0); в (m+1)-й строке этого столбца получаем значение целевой функции Z0=CбA0при этом плане.

Приведем алгоритм решения задачи симплекс-методом.

1. Находят опорный план X0 = (b1, b2,...,bm, 0,..., 0).

2. Составляют симплекс-таблицу типа 1.

3. Выясняют, имеется ли хотя бы одно Dj<0. Если нет таких чисел, то найденный опорный план будет оптимальным. В противном случае устанавливают либо неразрешимость задачи (все компоненты вектора Ajнеположительны), либо переходят к новому опорному плану.

4.

j 0

В новый план включают вектор As, для которого min (D Q ) , Dj

j

< 0, a

Q0 = bk / aks =

min (bi / ais) , ais > 0. Элемент aksявляется разрешающим, который и опре-

i

деляет базисный вектор Ek, подлежащий замене вектором As.

5. В новом базисе таблица пересчитывается так:

а) все элементы k-ой строки, начиная со столбца А0, делятся на aks;

б) все элементы столбца As заменяются нулями, кроме aks=1. Координаты остальных базисных векторов остаются неизменными;

*

в) любой элемент a ij

(j ¹ s) определяется по формуле:

a*=

1 (a a - a a )

akjais

= a -

(4)

ij

ks

ks ij kj is ij

a ks

a

- правило прямоугольника;

г) (m+1)-я строка вычисляется аналогично:

j

D*=

1 aks

(aksD j

- a kjDs)

= D j -

a kj

a ks

Ds .

6.

*

*

Если все D j

³ 0 , то полученный план оптимальный (составляется из ком-

понент Ao) и Zmax

= D0. В противном случае возвращаемся к п.4 алгоритма. После

конечного числа итераций получим оптимальный план или докажем отсутствие та- кого плана.

Задача 1.1. Решить симплекс-методом задачу: для изготовления различных изделий А, В, С предприятие использует три вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано пред- приятием, приведены в табл.2. Изделия А, В и С могут производиться в любых со- отношениях (сбыт обеспечен), но производство ограничено выделенным предприятию сырьем каждого вида. Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.

Таблица 2.

Вид сырья	Нормы затрат сырья (кг) на одно изделие	Общее количество сырья (кг)
	А	В	С
Цена одного изделия (руб.)

Решение. В векторной форме будем иметь

x1A1 + x2A2+ x3A3+ x4A4 + x5A5 + x6A6= A0, где

æ18ö

æ15ö

æ12ö

æ 1ö

æ 0ö

æ 0ö

.

æ 360ö

A1= ç 6 ÷ ,A = ç 4 ÷ , A

= ç 8 ÷ , A = ç ÷

,A = ç ÷

,A = ç ÷

, A =

ç ÷

ç ÷ 2 ç ÷

ç ÷ ç ÷

3 ç ÷

ç ÷

4 ç ÷

ç ÷

5 ç ÷

ç ÷

6 ç ÷

ç ÷

0 ç ÷

ç ÷

è 5 ø

è 3 ø

è 3 ø

è 0ø

è 0ø

è 1ø

è180ø

Среди векторов A4, A5, A6- единичные, их принимаем за базисные и, поло- жив x1=x2=x3=0, получаем начальный опорный план:

X0=(0, 0, 0 ,360, 192, 180).

Составляем симплексную таблицу для 1-ой итерации и вычисляем

Z0=CбA0=0, D1=Z1-c1=0-9=-9, D2=Z2-c2=-10, D3=Z3-c3=-16 и для векторов базиса

D4=D5=D6=0. Как видно, основные переменные x1, x2, x3 равны нулю, т.е. производ- ство не начато, прибыль Z0=0, и потому план X0не является оптимальным. Нахо- дим в каждом из столбцов A1, A2, A3

bi

Q j = mi n

i

aij

(j=1, 2, 3)

1 ç

Q = mi n æ 360,

192 ,

180ö

÷ = 20 =

b1

и Q1D1= -20 × 9 = -180 ,

i è 18 6 5 ø

a11

2 ç

Q = mi n æ 360,

192 ,

180ö

÷ = 24 =

b1

и Q2D2= -24 ×10 = -240 ,

i è 15 4 3 ø

a12

3 ç

Q = mi n æ 360,

192 ,

180ö

÷ = 24 =

b 2

и Q3D3= -24 ×16 = -384 .

i è 12 8 3 ø

a 23

Очевидно mi n (Q j D j ) =

j

Q3D3

= - 384 .

Поэтому вектор A3подлежит включению в базис вместо A5( Q3 = b2/a23, разрешающий элемент a23).

Составляем новую таблицу в базисе векторов A4, A3, A6. Для удобства поме- стим все итерации последовательно в одну табл. 3.

Таблица 3