Особенности обработки результатов моделирования. Требования, предъявляемые к качеству оценок
Особенность обработки результатов моделирования заключается в том, что:
- для анализа берутся результаты, полученные при работе имитационной модели на ЭВМ, что позволяет получить достаточно большую выборку по различным характеристикам исследуемого объекта;
- в процессе моделирования часто невозможно использовать априорную информацию о характеристиках процесса функционирования исследуемой системы, что приводит к использованию при анализе результатов непараметрических характеристик и моментов оценок;
- при исследовании каких-то характеристик имитационной модели часто приходится представлять переменные в виде удобном для их реализации на ЭВМ.
К качеству оценок, полученных в результате статистической обработки результатов моделирования, предъявляются следующие требования:
1) несмещенность оценки, т.е. равенство математического ожидания оценки определенному параметру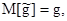 
где 
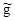- оценка переменной (параметра) g;
2) эффективность оценки, т.е. минимальность среднего квадрата ошибки данной оценки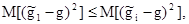 
где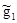 
- рассматриваемая оценка; 
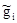- любая другая оценка;
3) состоятельность оценки, т.е. сходимость по вероятности при N ® ¥ к оцениваемому параметру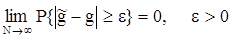 
, либо учитывая неравенство Чебышева, условие выполнения этого неравенства заключается в том, чтобы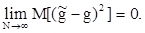 
Рассмотрим оценку выборочного среднего значения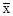 
. Математическое ожидание выборочного среднего значения 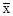составит
,
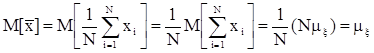т.е. оценка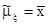 
является несмещенной.
С учетом независимости значений xi средний квадрат ошибки
,
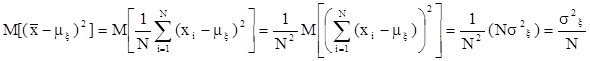т.е. оценка 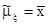является состоятельной. Также можно доказать, что эта оценка и эффективна.
Анализ и интерпретация результатов моделирования. Статистический анализ. Корреляционный анализ
Возможность фиксации при имитационном моделировании объектов и систем значений переменных (параметров) и их статистическая обработка для получения интересующих исследователя характеристик позволяет провести объективный анализ связей между этими величинами. Для решения этой задачи существуют различные методы, зависящие от целей исследования и вида получаемых при моделировании характеристик.
Статистический анализ
Математическое ожидание
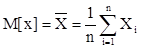, (15)
где n- объем выборки,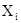 
- значение случайной величины.
Дисперсия является числовой характеристикой разброса случайной величины относительно ее математического ожидания и вычисляется по формуле
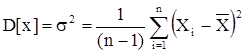. (16)
Среднее квадратичное отклонение (стандартное) является мерой стабильности результатов наблюдения и вычисляется по формуле
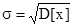. (17)
Коэффициент вариации вычисляется по формуле
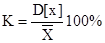. (18)
27.2 Корреляционный анализустанавливает, насколько тесна связь между двумя и более случайными величинами. Такой анализ сводится к оценке разброса значений случайной величины h (формирующие массив Y) относительно среднего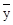 
, т.е. к оценке силы корреляционной связи. Существование этих связей и их тесноту можно выразить при наличии линейной связи между исследуемыми характеристиками и нормальности их совместного распределения.
Пусть результаты моделирования получены при N реализациях, а коэффициент корреляции
.
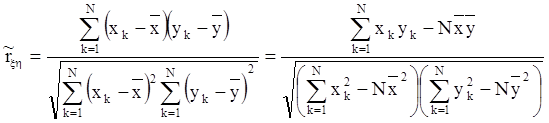Полученный при этом коэффициент корреляции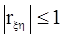 
. При сделанных предположениях rxh=0 свидетельствует о взаимной независимости случайных величин x
и h, исследуемых при моделировании. При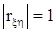 
имеет место функциональная (нестохастическая) линейная зависимость вида
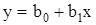, (19)
причем, если rxh>0, то говорят о положительной корреляции, т.е. большие значения одной случайной величины соответствуют большим значениям другой. Случай 0<rxh<1 соответствует либо наличию линейной корреляции с рассеиванием, либо наличию нелинейной корреляции результатов моделирования.