Подготовка прибора к работе и проведение измерений

Прибор включается в сеть кнопкой "СЕТЬ". Положение равновесия баллистического маятника устанавливается так, чтобы оно соответствовало нулю угловой шкалы.

Измерение периода колебаний баллистического маятника.

Подвижные грузы закрепите на расстоянии R₁, предложенном преподавателем. Обнулите показания прибора нажатием кнопки "СБРОС", аккуратно отклоните баллистический маятник на заданный преподавателем угол от положения равновесия и отпустите. По достижении баллистическим маятником числа колебаний «девять» (9), нажмите кнопку "СТОП". В этом случае прекращается счет времени после десяти полных колебаний. Период колебаний равен времени, деленному на количество колебаний (N = 10). Т = t/N.

Измерение угловой амплитуды при абсолютно неупругом ударе пули о мишень с пластилином баллистического маятника.

Установите подвижные грузы в предлагаемое положение (по указанию преподавателя). Зарядите специальной пулей зарядное пружинное устройство так, чтобы после сжатия пружины оно фиксировалось и удерживалось. Баллистический маятник с пластилиновой мишенью должен находиться в спокойном состоянии, соответствующем нулевому положению угловой шкалы. Нажав на затвор стреляющего устройства, зарегистрируйте максимальный угол, на который отклонился баллистический маятник.

После выстрела пуля должна застрять и оставаться в пластилиновой мишени. Такой опыт считается удачным. В случае, если пуля отскочила, установку необходимо привести в исходное состояние и опыт повторить.

Баллистическая идея измерения скорости пули заключается в том, что за время соударения пули с маятником угловая скорость баллистического маятника изменяется достаточно заметно, а его угловое перемещение незначительно и им можно пренебречь. Естественно, что это условие выполняется в том случае, если масса маятника намного больше массы пули.

Скорость пули определяется по измерению максимального угла отклонения маятника после неупругого соударения с пулей. Процесс неупругого соударения пули с маятником описывается на основе закона сохранения момента импульса (в этом процессе механическая энергия не сохраняется!), а процесс последующего движения может быть описан с помощью закона сохранения механической энергии.

Однако любая теоретическая модель является лишь приближенным описанием физической ситуации, так как пренебрегает влиянием многих эффектов, имеющих место в эксперименте. Но если пренебрежения реальными эффектами в теоретической модели не изменяют конечного результата больше чем на 1/20 от его реального значения, то такая теоретическая модель в лабораторном физическом практикуме является вполне приемлемой и позволяет определить искомую физическую величину.

В нашем случае мы пренебрегаем незначительным смещением центра масс маятника после соударения с пулей, упругими колебаниями, которые при этом возникают и, соответственно, перераспределением механической энергии между крутильными и упругими колебаниями. Также считаем крутильные колебания незатухающими, пренебрегая сопротивлением воздуха и диссипацией энергии неупругих колебаний в местах подвеса упругой проволоки и т. п. Тем не менее, предложенная теоретическая модель позволяет получить вполне хорошие результаты.

Задание 1. Определение момента инерции баллистического маятника (I_о) и коэффициента упругих сил кручения (C).

1. Установите подвижные грузы массой М на одинаковом расстоянии d₁от оси вращения. Отклонив баллистический маятник на угол φ ~ 20°, измерьте период колебаний Т_1. Повторите опыт 3 раза и вычислите среднее значение T₁.

2. Установите положение подвижных грузов массой М на расстоянии d₂ и повторите опыт (см. задание 1). Лучше, если значения d₁ и d₂ отличаются как можно больше.

3. Из системы уравнений 1) и 2), подставив численные значения Т₁, Т₂, d₁, d₂, найдите I_о и С.

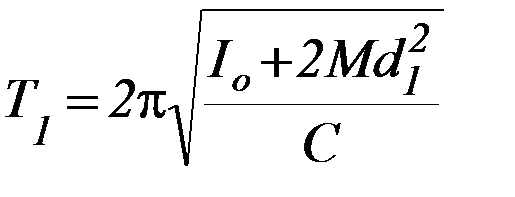(1)

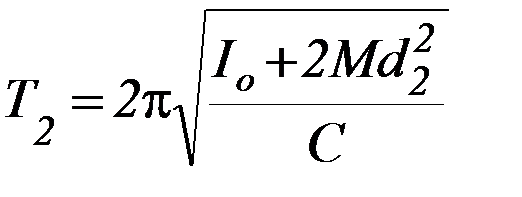(2)

4. Рассчитайте относительную погрешность определения момента инерции и коэффициента упругих сил кручения ,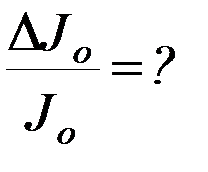

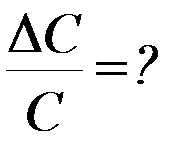
В силу сложности математического выражения для определения данной погрешности, можно воспользоваться упрощённым вариантом расчёта. Для этого относительные погрешности прямым образом определяемых величин (M, d, T) принять равными: 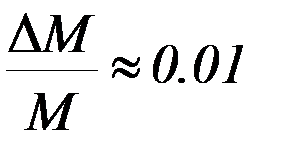; 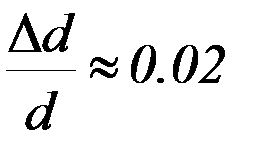. (В данной работе период рассматриваем как прямым образом измеренную величину). Относительная погрешность измерений в данной установке периода: 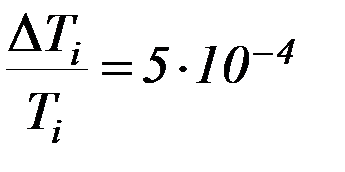, и ею можно пренебречь. Рассчитать относительную погрешность определениямомента инерции и коэффициента упругих сил кручения как сумму относительных погрешностей прямым образом определяемых величин.

Задание 2. Определение скорости пули (V_п) и угловой скорости вращения (W).

1. Зарядите стреляющее устройство и, установив подвижные грузы (М) на одинаковом расстоянии d₃, произведите выстрел, измерив при этом максимальное отклонение баллистического маятника φ_max и расстояние от оси вращения до центра масс пули .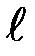

2. Закон сохранения момента импульса даёт:

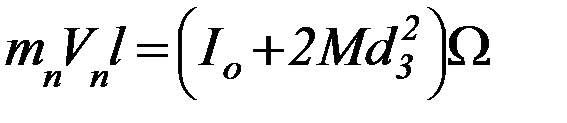(3)

где V_п – скорость пули, – угловая скорость системы после удара.

Закон сохранения механической энергии:

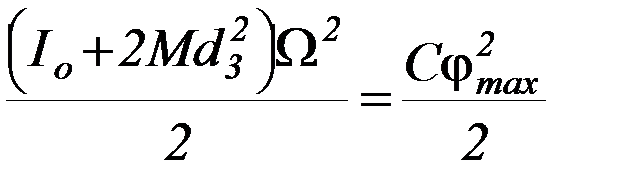(4)

Из системы уравнений 3) и 4) найдите W и V_п. Угол φ_max при этом нужно подставить в радианах:

,

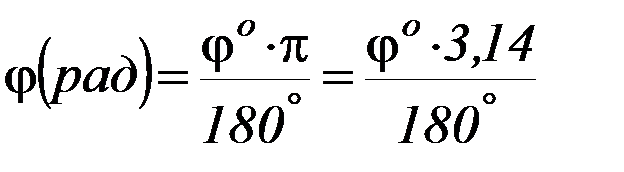где φ^о – угол в градусах.

Рассчитайте относительные погрешности скорости пули 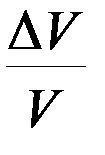и угловой скорости вращения .

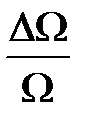Относительные погрешности прямым образом определяемых величин (m, φ_m, 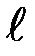) принять равными: 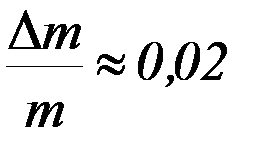; ; 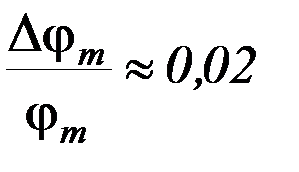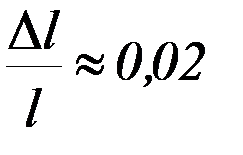. Рассчитайте относительную погрешность скорости пули и угловой скорости вращения как сумму относительных погрешностей прямым образом определяемых величин.