Исследование статистических закономерностей биномиального распределения методом моделирования на эвм

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное образовательное учреждение высшего профессионального образования

«Чувашский государственный университет имени И.Н. Ульянова»

МОЛЕКУЛЯРНАЯ ФИЗИКА.

Лабораторные работы

Чебоксары

УДК 53(075.8) Составители:

А.Л. Иванов

О.В. Филиппова

Молекулярная физика: Лабораторные работы.

/Сост. А.Л. Иванов, О.В. Филиппова; Чуваш. ун-т. Чебоксары, 2013., с.84.

Содержат лабораторные работы раздела курса общей физики «Молекулярная физика», основные формулы, вопросы к лабораторным работам, список используемой литературы. Для студентов I курса физико-технического факультета.

Отв. редактор профессор Г.Г. Телегин

Утверждено Методическим советом университета

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Федеральное государственное образовательное учреждение высшего

профессионального образования

«Чувашский государственный университет имени И.Н. Ульянова»

МОЛЕКУЛЯРНАЯ ФИЗИКА.

Лабораторные работы

Чебоксары

ОГЛАВЛЕНИЕ

I. Лабораторная работа №2. Исследование статистических закономерностей биномиального распределения методом моделирования на ЭВМ. 6

II. Лабораторная работа № 4. Измерение теплоемкости металлов и параметров естественной конвекции методом охлаждения. 19

III. Лабораторная работа № 5 Определение отношения удельных теплоемкостей газов методом адиабатического расширения. 26

IV. Лабораторная работа №6. Определение отношения удельных теплоемкостей по скорости звука в газе. 31

V. Лабораторная работа № 7. Определение коэффициента теплопроводности воздуха. 35

VI. Лабораторная работа № 10. Определение коэффициента внутреннего трения газа капилярным вискозиметром. 40

VII. Лабораторная работа № 12. Определение коэффициента внутреннего трения по методу стокса. 43

VIII. Лабораторная работа № 21. Изучение критического состояния вещества. 55

IX. Лабораторная работа № 23. Определение теплоты испарения жидкости по зависимости давления насыщенного пара от температуры.. 60

Приложение 1……………………………………………….…….74

Приложение 2…………………………………………………......75

Приложение 3………………………………………..……………77

Молекулярная физика

Лабораторные работы.

Отв. за выпуск Л.Г. Григорьева

Подписано в печать 4.10.2011г. Формат 60 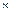80/16. Бумага газетная. Офсетная печать. Гарнитура Таймс. Усл.печ. л. 3,25. Усл.-изд. л.3,0. Тираж 100 экз. Заказ №444 .

Чувашский государственный университет

Типография университета

428015 Чебоксары, Московский просп.15

I. Лабораторная работа №2.

ИССЛЕДОВАНИЕ СТАТИСТИЧЕСКИХ ЗАКОНОМЕРНОСТЕЙ БИНОМИАЛЬНОГО РАСПРЕДЕЛЕНИЯ МЕТОДОМ МОДЕЛИРОВАНИЯ НА ЭВМ.

ЦЕЛЬ РАБОТЫ: 1. Ознакомление с функциями распределения.

2. Исследование статистических закономерностей биномиального распределения методом моделирования на ЭВМ рассеяния горошин на системе решеток.

ОБОРУДОВАНИЕ: компьютер, программа MF2.

1.ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ.

1.1 СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

Результат любого случайного, то есть заранее достоверно не предсказуемого эксперимента можно охарактеризовать качественно и количественно. Качественный результат случайного эксперимента - это случайное событие, которое может произойти, или не произойти: например, тарелка при падении на пол разбилась, либо не разбилась. Вероятность случайного события – это предел отношения числа экспериментов, в результате которых это событие произошло, к общему числу экспериментов, когда общее число экспериментов стремиться к бесконечности.

Любая количественная характеристика, которая в результате случайного эксперимента (измерения) может принять одно из некоторого множества значений, - это случайная величина. Обозначим: X - случайная величина, x – её возможные значения.

Каждая случайная величина полностью определяется своей функцией распределения. Функцией распределения случайной величины называется функция F(x), равная вероятности того, что в результате эксперимента эта величина примет значение меньшее, или равное x.

Функция распределения F(x) определена на всей числовой оси и является неубывающей функцией x, возрастающей от F(x_min) = 0 на нижней границе x_min возможных значений x до F(x_max) = 1 на верхней границе x_max.

Выполнив N экспериментов можно получить набор из N значений x_j случайной величины X, где j=1, 2,…, N. Этот набор так же является случайным, и называется случайной выборкойслучайной величины X.

По случайной выборке можно найти среднее арифметическое значение <x> для этой выборки (среднее выборочное):

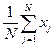< x >= (I.1)

Поскольку среднее значение вычисляется по случайным значениям x_j, оно само является случайной величиной. Однако, когда число экспериментов N стремится к бесконечности, <x> стремится к некоторому пределу, который называется математическим ожиданием 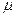x= 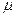случайной величины X

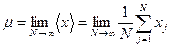(I.2)

Набор результатов такого бесконечного числа экспериментов называется генеральной выборкойслучайной величины X.

Результаты x_j экспериментов случайным образом отличаются от 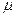. Характеристиками величины их разброса в случайной выборке из N экспериментов являются среднеквадратичное отклонение σx= σ случайной величины X от математического ожидания 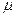и дисперсия Dx= D =σ²:

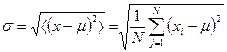(I.3)

Если математическое ожидание 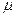неизвестно, вместо него можно использовать среднее значение <x>, найденное по значениям x_j из этой же случайной выборки, но при этом вместо N в формуле нужно делить на N-1:

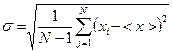(I.4)

Среднеквадратичное отклонение σ, вычисленное по случайной выборке, тоже будет случайной величиной. Достоверное значение σ можно получить только по генеральной выборке, то есть при N→∞.

Если провести множество серий измерений по N измерений в каждой серии, и каждую из этих серий считать одной случайной выборкой, то по каждой случайной выборке по формуле (I.1) можно вычислить среднее арифметическое значение <x>. Эти <x> будут случайным образом отличатся и друг от друга, и от математического ожидания 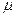. При этом в суммах в формуле (I.1) будут присутствовать слагаемые x_j, как превышающие 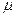, так и меньшие чем 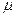. В результате произойдет частичная компенсация их случайных отклонений, и средние арифметические значения <x> окажутся значительно ближе к математическому ожиданию 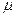, чем результаты отдельных измерений x_j.

Можно доказать, что среднеквадратичное отклонение σ<x> среднего арифметического значения <x> от математического ожидания обратно пропорционально 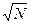, а для большого числа серий по N измерений выполняется соотношение:

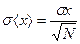(I.5)

То есть среднее арифметическое по выборке из N измерений в 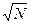раз точнее результата одного измерения.

1.2 ДИСКРЕТНАЯ И НЕПРЕРЫВНАЯ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

Дискретная случайная величина может принимать значения из некоторого дискретного числового множества. Например, число очков, выпавших при бросании кубика, принимает значения из дискретного числового множества {1, 2, 3, 4, 5, 6}. На числовой оси разрешенные (возможные) значения отображаются точками, отделенными друг от друга запрещенными промежутками. При этом весь интервал разрешенных значений можно разбить на такие маленькие кусочки, в каждом из которых будет не более одного разрешенного значения. Эти значения можно пронумеровать в порядке возрастания: x₁ < x₂ < … < x_i < … x_n, где n – конечное или бесконечное число возможных значений. Каждое из этих значений имеет, соответственно, свою вероятность: p_1, p_2, …, p_i … Совокупность значений p_i =p( x_i) называется распределением дискретной случайной величины(не путать с функцией распределения!). Функция распределения F(x) дискретной случайной величины ступенчатая, скачком изменяющаяся на p_i при переходе через каждое x_i. Для любого данного значения x она равна сумме вероятностей p_i всех возможных значений x_i ≤ x.

Распределение дискретной случайной величины подчиняется условию нормировки – сумма вероятностей всех возможных значений равна 1:

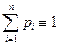(I.6)

Зная распределение дискретной случайной величины, можно найти математическое ожидание и дисперсию:

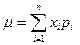, (I.7),

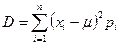(I.8)

Непрерывная случайная величина может принимать любые значения в некотором разрешенном интервале x_min ≤ x ≤ x_max. Например, вес случайно выбранного человека. На числовой оси на сколь угодно маленьком промежутке разрешенного интервала имеется бесконечно большое число возможных значений непрерывной случайной величины, и вероятность получения любого заданного значения х равна нулю. Поэтому для непрерывных случайных величин вместо вероятности P_i получения отдельного значения x_i используют вероятность ΔP(x, Δx) получения любого значения случайной величины в интервале от x до x + Δx.

Предел отношения:

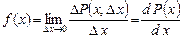(I.9)

называется плотностью вероятности случайной величины x.

В термодинамике плотность вероятности принято называть функцией распределения.

Чтобы плотность вероятности f(x) не путать с другой функцией распределения F(x), их обозначают разными буквами: f(x) и F(x). Друг с другом они связаны соотношениями:

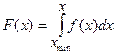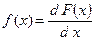, (I.10)

Поэтому F(x) иногда называют интегральной функцией распределения, а f(x) - дифференциальной функцией распределения.

Если известна функция f(x), или F(x), то можно найти вероятность получения значения случайной величины X в любом интервале от x₁ до x₂:

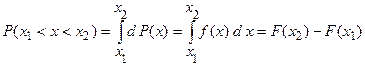(I.11)

Плотность вероятности f(x) подчиняется условию нормировки (сравните с I.6):

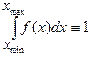(I.12)

Примером функции распределения непрерывной случайной величины х в интервале от - ∞ до + ∞ является функция нормального распределения Гаусса:

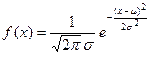(I.13).

Функция Гаусса имеет максимум при х = µ и монотонно уменьшается, стремясь к нулю, при удалении от точки х = µ .

Функция Гаусса реализуется в тех случаях, когда значение случайной величины х зависит от большого числа независимых случайных факторов. Функцией Гаусса описывается, например, распределение молекул идеального газа по компонентам скоростей V_x, V_y, V_z.

Зная функцию распределения, можно найти математическое ожидание и дисперсию (сравните с I.14, I.15):

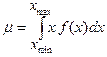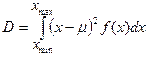, (I.14),(I.15).

2. ОПИСАНИЕ ИСПОЛЬЗУЕМОЙ МОДЕЛИ.

2.1 ОБЩЕЕ ОПИСАНИЕ.

В компьютерном эксперименте по экрану монитора из источника, находящегося в левой части экрана, движется поочередно слева направо заданное число горошин, проходя через систему из m вертикально расположенных решеток. На каждой решетке горошины испытывают случайное отклонение по вертикали на -1(вверх) или на +1(вниз) с равной вероятностью p=0,5. Пройдя через m решеток, горошина m1 раз испытывает смещение на +1 и m2 раза на -1, причем m1+ m2= m. При этом заранее неизвестно, сколько раз и на каких решетках произойдет у данной горошины смещение в ту или другую сторону. Суммарное смещение горошины:

х = m1*(+1) +m2*(-1) =m1- m2 может принимать m+1 различных случайных значений в интервале от – m до + m. При этом, если m четно (нечетно), то и все возможные значения х четны (нечетны).

После решеток горошины попадают в ячейки, находящиеся в правой части экрана. Каждому возможному значению смещения х соответствует своя ячейка. Общее число горошин и число горошин, попавших в каждую ячейку, подсчитываются и печатаются на экране монитора в течение всего эксперимента. После завершения эксперимента компьютер производит обработку полученных результатов и выводит их на экран в виде таблиц и графиков.

2.2 СТАТИСТИЧЕСКИЕ ЗАКОНОМЕРНОСТИ ДЛЯ ЧИСЛА ГОРОШИН В ОДНОЙ ПРОИЗВОЛЬНОЙ ЯЧЕЙКЕ.

Введем следующие обозначения: n - общее число горошин, участвовавших в данном эксперименте, n_i, (где i=1,2,3,…,m+1) - число горошин, испытавших смещение на x = x_i и попавших в i-ю ячейку, y_i =n_i/n - доля горошин, попавших в i-ю ячейку.

Число горошин n_i и доля горошин y_i , попавших в i-ю ячейку, являются случайными числами. Однако при очень большом числе горошин доля горошин стремится к своему пределу - вероятности p_i попадания горошины в i-ю ячейку:

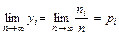(I.16).

При многократных повторениях эксперимента в одинаковых условиях (в данном случае при одинаковых m и n) можно заметить следующие закономерности:

-Доли горошин y_i , попавших в i-ю ячейку принимают случайные значения, преимущественно близкие к p_i.

-Меньшие отклонения y_i от p_i встречаются чаще, чем большие.

По результатам N экспериментов можно найти среднее число горошин <n_i> и среднюю долю горошин <y_i>, попавших в i-ю ячейку:

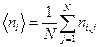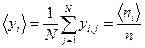, (I.17),

где n_i,j и y_i,j ─соответственно число горошин и доля горошин, попавших в i-ю ячейку в j-м эксперименте. В пределе, когда число повторений эксперимента N стремится к бесконечности, числа <n_i> и < y_i> стремятся к своим пределам:

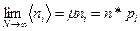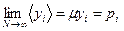, (I.18) ,

где 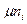- математическое ожидание для числа горошин в i-й ячейке, а для доли горошин y_i в i-й ячейке математическое ожидание 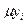равно вероятности p_i попадания горошин в i-ю ячейку. Вероятность p_i для данного x_i может быть найдена по (I.24) ,

Среднеквадратичное отклонение σn_i числа горошин в i-й ячейке от математического ожидания :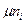

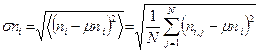(I.19)

Среднеквадратичное отклонение σy_i. доли горошин в i-й ячейке от её математического ожидания 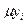=p_i:

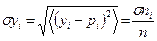(I.20).

Среднеквадратичное отклонение σn_i зависит от общего числа горошин n. При увеличении n σn_i тоже возрастает, но медленнее чем n: σn_i ~ 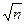. При этом среднеквадратичное отклонение σy_i уменьшается: σy_i ~ .

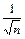В частном случае, когда число горошин n→∞, а число решеток m достаточно велико и доля y_i горошин, попавших в i-ю ячейку мала (y_i<<1) среднеквадратичные отклонения числа горошин σn_i в i-й ячейке и доли горошин σy_i в i-й ячейке выражаются через число горошин:

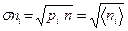(I.21).

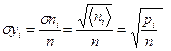(I.22).

Отсюда следует, что погрешность экспериментального определения вероятностей p_i по формуле (I.16) обратно пропорциональна .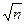

Найдем из (I.21) и (I.22) относительные среднеквадратичные отклонения:

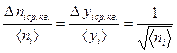(I.23).

2.3. СТАТИСТИЧЕСКИЕ ЗАКОНОМЕРНОСТИ ДЛЯ РАСПРЕДЕЛЕНИЯ ГОРОШИН ПО ЯЧЕЙКАМ.

При рассеянии горошин на системе решеток различные смещения х встречаются с различной вероятностью. Совокупность вероятностей p_i = p(x_i) = p(x) для всех возможных значений смещений x составляет функцию распределения смещений горошин. При оговоренных в разделе 2.1 условиях машинного эксперимента результирующее смещение x горошины получится, если на 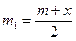решетках произойдет смещение на +1, а на 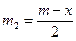решетках произойдет смещение на -1.

Распределение горошин по ячейкам выражается формулой:

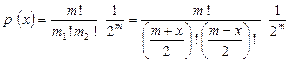(I.24),

Функция (I.24) является симметричной и монотонно уменьшается при увеличении модуля х.

Формула (I.24) является частным случаем биномиального распределения:

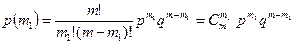(I.25),

где р и q = 1 - p - вероятности смешения горошин на каждой отдельной решетке соответственно на +1 и -1 , 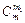–число возможных перестановок m₁ неразличимых предметов по m местам. При подстановке p = q = 0,5 , m - m₁ = m₂ формула (I.15) переходит в (I.24).

Величины, стоящие в правой части (I.25) являются слагаемыми известного разложения суммы двух чисел p и q в степени m по формуле бинома Ньютона:

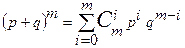(I.26).

Поскольку p + q = 1 из (I.26) следует, что для функции распределения (I.25) выполняется условие нормировки (I.6).

Биномиальному распределению (I.25) подчиняется, например, случайное число m₁ молекул газа, находящихся в произвольный момент времени в некотором выделенном объеме V₁ всего объема V системы, содержащей m молекул. В этом случае p = V₁/V – вероятность нахождения любой выбранной молекулы в объеме V₁, q = 1-p – вероятность ее нахождения вне объема V₁ (но внутри объема V).

При больших m функция (I.25) имеет острый максимум вблизи среднего числа <m₁>=m·p молекул в объеме V₁.

При большом числе решеток m→ ∞ распределение горошин по смещениям приближаются к функции Гаусса (I.13):

P_i = f(x_i) Δx, (I.28).

где Δx = 2 , f(x_i) рассчитывается по функции Гаусса (I.13) при µ = 0, 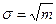(см. (I.33)).

Для каждого эксперимента по полученным значениям смещений горошин x_i можно найти среднее смещение 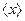, которое так же является случайной величиной, но при увеличении числа горошин n→ ∞. оно стремится к постоянному пределу - математическому ожиданию смещения горошин µx_.. Поскольку вероятности смещения на +1 и на -1 одинаковы, математическое ожидание µx_. =0. При увеличении числа горошин n среднеквадратичное отклонение среднего смещения 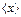от математического ожидания уменьшается обратно пропорционально 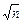(сравните с (I.5).

Найдем дисперсию Dx = D и среднеквадратичное отклонение σx = σ случайного смещения горошин х в исследуемой модели при числе горошин n→∞. Запишем общее смещение в виде суммы случайных смещений ξ _j на отдельных решетках:

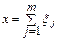, (I.29).

где j=1, 2, … , m - номер решетки, смещения ξ_j принимают значения +1 или -1 с вероятностью 0,5.

Согласно (I.3) с учетом µx = 0:

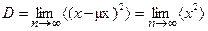, (I.30).

где: 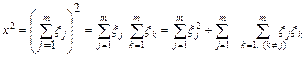(I.31).

При нахождении в (I.30) среднего значения 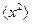в пределе при n→ ∞ вторая сумма в (I.31) обращается в 0, поскольку смещения ξ _j и ξ _k на разных решетках независимы друг от друга и с равной вероятностью могут быть одинакового или противоположного знака. Поэтому, с учетом 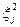=1, остается:

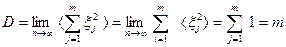. (I.32).

Среднеквадратичное отклонение 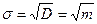(I.33).

3. ПРОВЕДЕНИЕ КОМПЬЮТЕРНОГО ЭКСПЕРИМЕНТА С ПРОГРАММОЙ MF2.

Для проведения эксперимента вводятся следующие данные:

1. Число решеток (от 1 до 20).

2. Общее число горошин (от 1 до 10000).

3. Число горошин в серии (от 1 до общего числа горошин).

4. Скорость движения горошин (от 0 до 10).

Последние два данных на результаты эксперимента не влияют и выбираются из условия удобства наблюдения за ходом эксперимента.

После ввода данных автоматически начинается эксперимент.

После завершения эксперимента на экране появляется сообщение:

1. Запомнить и обработать результаты эксперимента.

2. Возврат в меню.

При нажатии клавиши ’’2’’ результаты проведенного эксперимента уничтожаются, и происходит возврат в меню. При нажатии клавиши ’’1’’ производится обработка результатов эксперимента и вывод их на экран в виде таблицы и графика. В таблице приводятся значения координат ячеек x; числа горошин, n(x), попавших в каждую ячейку; доля горошин y(x) от общего числа; значения аппроксимирующей функции Гаусса (I.13) в точках x, соответствующих координатам ячеек и значения биномиальной функции распределения (I.24) для данного числа решеток.

Функция Гаусса рассчитывается для среднеквадратичного отклонения горошин, полученного в данном эксперименте:

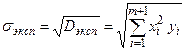
На графике в одинаковом масштабе приводятся распределение горошин по ячейкам, биномиальная функция и функция Гаусса.

4. . ПОРЯДОК ВЫПОЛНЕНИЯ ЭКСПЕРИМЕНТАЛЬНОЙ ЧАСТИ РАБОТЫ.

Упражнение.1. Исследование статистических закономерностей для числа горошин в одной ячейке.

Для указанного преподавателем числа решеток m провести 5 экспериментов с большим n ≥ 1000 числом горошин. В каждом j-м эксперименте записать число горошин n_{i, j}, попавших в указанную преподавателем i-ю ячейку.

По полученным результатам рассчитать среднее число горошин <n_i>, попавших в i-ю ячейку, и среднюю долю горошин <y_i>. Полученные значения сравнить с математическими ожиданиями µx_i и p(x_i).

Рассчитать среднеквадратичное отклонения числа горошин в i-й ячейке от среднего арифметического:

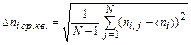
и относительное среднеквадратичное отклонение числа горошин .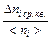

Полученные значения нения сравнить с 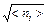и 1/ .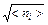

Сформулировать выводы.

Упражнение.2. Исследование статистических закономерностей распределения горошин по ячейкам при различном числе решеток.

По указанию преподавателя провести эксперименты с большим числом горошин ( n 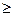2000 ) и различным числом решеток m: малым ( m = 2 – 5 ), средним ( m = 6 – 10 ) и большим ( m = 10 – 20). В каждом эксперименте провести обработку результатов, таблицы результатов переписать в тетрадь, по точкам из таблицы построить графики.

Сравнить экспериментальные y(x), биномиальные и Гауссовы функции распределения для различных чисел решеток и между собой. Сравнить полученные дисперсии с числом решеток. Сформулировать выводы.

Упражнение.3. Исследование статистических закономерностей распределения горошин по ячейкам при различном числе горошин.

По указанию преподавателя провести эксперименты с большим числом решеток m 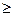10 и различным числом горошин: малым (n = 10 – 20), средним (n = 100 – 500) и большим (n 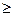1000). Провести обработку экспериментов, переписать таблицы и построить графики.

Сравнить экспериментальные y(x), биномиальные и Гауссовы функции распределения для различных чисел горошин и между собой. Сформулировать выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. Что общего и в чем различие между средним значением и математическим ожиданием случайной величины?

2. Основные параметры дискретных и непрерывных случайных величин. Как они находятся?

3. Как зависит погрешность экспериментально определенной функции распределения горошин по ячейкам от общего числа горошин.

4. Где реализуется биномиальная функция распределения?

5. В каких случаях применима функция распределения Гаусса.

ЛИТЕРАТУРА.

А.Н. Матвеев. Молекулярная физика. М. “Высшая школа” 1981 г. с. 18 – 35, 43 – 55, 55 – 60.

II. Лабораторная работа № 4.
Измерение теплоемкости металлов и параметров естественной конвекции методом охлаждения.

1. Основные понятия.

Теплоёмкостью тела С_тела называется отношение бесконечно малого количества тепла 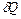, полученного телом, к вызванному этим приращению его температуры dT. Удельной теплоемкостью с (с- малое) называется теплоемкость единицы массы вещества, молярной теплоемкостью С (С- большое) называется теплоемкость одного моля:

С_тела= 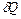/dT; 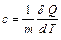; 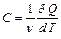(II.1)

где m- масса тела, ν число молей, причем С= μ*с, где μ - молярная масса. Теплоемкость зависит от условий нагрева или охлаждения. При этом наиболее часто используются теплоемкость при постоянном объёме:

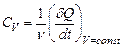; ( аналогично С_тела и С_V ),

и теплоемкость при постоянном давлении

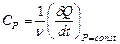; ( аналогично С_тела и С_р ).

Между С_р и С_V существует соотношение:

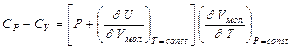
где V_мол- молярный объём, U- внутренняя энергия, 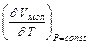- температурный коэффициент объемного расширения.

С_р больше чем С_v на величину работы ,совершаемой при нагревании 1 моля тела на 1К, против внешнего давления Р и внутреннего давления Р_i= 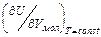, обусловленного силами взаимодействия между молекулами тела. Для идеального газа С_р-С_v=R - соотношение Роберта Майера, а для твердых и жидких тел ввиду малости температурного коэффициента объемного расширения С_р и С_v практически равны. Теплоемкость зависит от химического состава, строения молекул тела. Обычно при увеличении температуры теплоемкость также возрастает. Теплоемкость С_v можно выразить через средние числа задействованных степеней свободы молекул тела:

С_v=(i_пост+i_вр+2*i_колеб)*R/2=i_эфф*R/2 (II.2)

где i_пост ,i_вр, i_колеб - средние числа поступательных, вращательных и колебательных степеней свободы, которые могут принимать тепловую энергию при данных условиях. i_эфф - эффективное число степеней свободы. Например в газах, при нормальных условиях, задействованы только поступательные (i_пост=3) и вращательные степени свободы (i_вр.=0 для одноатомных, i_вр.=2 для линейных и i_вр.=3 для нелинейных молекул). Для возбуждения колебательных степеней свободы молекул газов при н.у. энергии теплового движения недостаточно. Соответственно С_v= 3/2R; 5/3R; 6/2R для газов с одноатомными, линейными и нелинейными молекулами.

В твердых телах, наоборот, молекулы могут совершать только колебательные движения около своих положений равновесия. При этом на каждый атом приходится при достаточно высоких температурах 3 колебательные степени свободы, и согласно закону Дюлонга-Пти теплоемкость Сv твердых тел равняется: С_v=3nR, где n - число атомов в молекуле.

2. ТЕОРИЯ МЕТОДА.

Предлагаемый метод измерения теплоемкости металлов основан на сравнении скоростей естественного охлаждения в одинаковых условиях одинаковых по форме и размеру образцов из исследуемого и эталонного металлов, предварительно нагретых до некоторой начальной температуры Т_нач.

Если температура тела Т отличается от температуры окружающей среды Т₀ , то между телом и средой происходит теплообмен.

Существует три механизма теплообмена:

1. Теплопроводность -это теплообмен за счет теплопроводности окружающей среды (при этом среда остается неподвижной относительно тела). При небольшой разности температур количество тепла 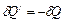, отданного телом в окружающую среду за время t, выражается законом теплоотдачи Ньютона:

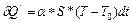(II.3)

где S - площадь поверхности тела. 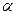- коэффициент теплоотдачи, зависящий от формы тела, температур Т₀ и Т, давления и состава окружающей среды. Для газов 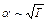и практически не зависит от давления.

2. Конвекция - это теплообмен за счет теплопроводности ближайших к телу слоев окружающей среды, которые тут же уносятся от образца в результате движения самой среды относительно тела. Конвекция называется искусственной, если движение среды вызвано внешними причинами (например, работающим вентилятором) и естественной - если среда приводится в движение за счет разности выталкивающих сил Архимеда и сил тяжести, действующих на различные слои среды, при наличии температурного градиента около тела. Естественная конвекция возникает скачком при достижении некоторой критической разности температур Т и Т₀. При этом резко возрастает интенсивность теплообмена, который при конвекции описывается уравнением

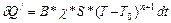(II.4)

где В и n (n>0), - параметры, зависящие от формы тела и свойств окружающей среды, 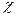- теплопроводность воздуха при температуре Т.

3. Тепловое излучение - это теплообмен за счет испускания и поглощения телом теплового электромагнитного излучения. При этом теплообмен описывается уравнением Стефана-Больцмана:

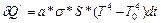
где 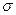- постоянная Стефана-Больцмана, a- усредненный коэффициент поглощения электромагнитного излучения поверхностью тела (а=1 для абсолютно черного тела, для всех реальных тел 0 < a < 1).

Тепловое излучение вносит заметный вклад в теплообмен только при высоких температурах и в настоящей работе им можно пренебречь.

Теплопроводность и конвекция не зависят от состава тела, поэтому и для исследуемого образца и для эталона, если они имеют одинаковые размеры, количество отдаваемого в окружающую среду тепла будет описываться одной и той же функцией:

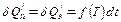(II.5).

Из (II.1) и (II.5), учитывая, что 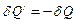, можно найти скорость охлаждения 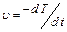для исследуемого образца (n) и для эталона (э):

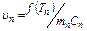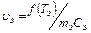; (II.6).

При одинаковых температурах Т_n = Т_э = Т:

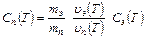(II.7).

По формуле (II.7) можно рассчитать теплоемкость исследуемого образца при различных температурах Т, если известны теплоемкости эталона при этих температурах.

Скорости охлаждения υ_n(T) и υ_э(Т) можно найти по наклону касательных к графикам охлаждения Т_n(t) и T_э(t) в точках, соответствующих температуре Т.

Практически из-за того, что скорость охлаждения быстро убывает по мере уменьшения температуры, вместо графиков охлаждения Т(t) в линейной шкале температур удобно воспользоваться логарифмическими графиками охлаждения

y = ln (T-T₀ ) = f(t),

на которых у почти линейно убывает с течением времени.

Модуль тангенса угла наклона касательной в точке, соответствующей температуре Т для кривой равен:

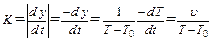(II.8).

Тогда при одинаковых температурах Т_n = Т_э = Т

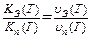
и вместо (II.7) получим:

.

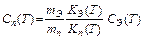3.МЕТОДИКА ОПРЕДЕЛЕНИЯ ПАРАМЕТРОВ ЕСТЕСТВЕННОЙ КОНВЕКЦИИ.

По графику охлаждения эталонного образца можно определить параметры В и n естественной конвекции в условиях опыта. Сравнивая (II.4) и (II.5) и используя (II.6) и (II.8) получим:

В χ S (T-T₀)ⁿ⁺¹ = m с υ = m с K (T-T₀).

Отсюда для эталонного образца

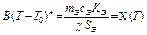(II.9),

где Х (Т) можно рассчитать для различных температур по экспериментально полученным значениям К_э для эталона, известным из справочника значениям удельной теплоемкости с_э и коэффициента теплопроводности воздуха χ_э при этих температурах.

Если из справочника известна теплопроводность воздуха при температуре Т₁, теплопроводность при других температурах Т можно найти по формуле

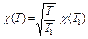
Для нахождения параметров В и n удобно воспользоваться графическим методом. Логарифмируем (II.4):

ln Х = ln В + n ln (Т-Т₀) (II.10).

Из (II.10) видно, что зависимость ln Х от ln (Т-Т₀) линейная, причем начальное значение ln Х (при ln (Т-Т₀)=0) равно ln В, а угловой коэффициент этой зависимости равен n.

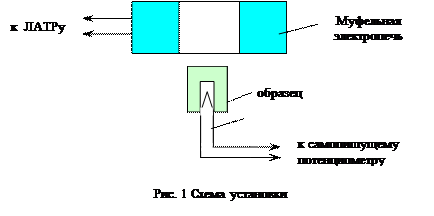
ОПИСАНИЕ УСТАНОВКИ

На рис.1 изображена схема установки. Исследуемые образцы представляют собой цилиндры с высверленным с одного конца каналом. В этот канал помещают хромель-алюмелевую термопару. Концы термопары подведены к самопишущему потенциометру, который автоматически записывает на диаграммной ленте зависимость температуры образца от времени.

Порядок выполнения работы.

1. Взвесить образцы меди, алюминия и железа.

2. Включить тумблер «сеть» самопишущего потенциометра, дать прогреться потенциометру не менее 5 минут, измерить температуру воздуха Т₀ вблизи термопары.

3. Ручкой подстроечного резистора «уст 0» выставить каретку потенциометра на 0^о С, когда термопара находится при комнатной температуре. В этом случае потенциометр будет показывать по шкале и записывать на диаграммную ленту разность ∆Т = Т – Т₀