Начальные и граничные условия

Продуктивный пласт или выделенную из него часть можно рассматривать как некоторую область пространства, ограниченную поверхностями – границами. Границы могут быть непроницаемыми для жидкостей или газов, например кровля и подошва пласта, сбросы и поверхности выклинивания. Граничной поверхностью является также поверхность, по которой пласт сообщается с областью питания (с дневной поверхностью, с естественным водоемом) – это контур питания; стенка скважины является внутренней границей пласта.

Чтобы получить решение системы уравнений, к ней необходимо добавить начальные и граничные (краевые) условия.

Начальное условие заключается в задании искомой функции во всей области в некоторый момент времени, принимаемый за начальный. Например, если искомой функцией является пластовое давление, то начальное условие может иметь вид:

p = pо(х, у, z) при t = 0,

(1.62)

то есть в начальный момент задается распределение давления во всем пласте.

Если в начальный момент пласт невозмущен, то начальное условие примет вид:

р = рk = const при t = 0.

(1.63)

Граничные (краевые) условия задаются на границах пласта. Число граничных условий должно быть равно порядку дифференциального уравнения по координатам.

Возможны следующие граничные условия.

Граничные условия первого рода. На границе задаются значения давления:

рêг = р(Г, t).

(1.64)

Граничные условия второго рода. На границе задаются значения нормальной скорости к границе:

unêг = un(Г, t).

(1.65)

Так, как по закону Дарси скорость фильтрации связана с градиентом давления, то это граничное условие можно записать в следующем виде:

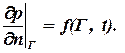(1.66)

Граничные условия третьего рода. Это граничное условие является комбинацией первых двух и в практике встречается редко. Граничные условия третьего рода записываются в виде:

.

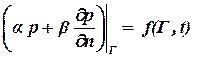(1.67)

Рассмотрим граничные условия в случае притока к галерее. Галерея имеет две границы: – одна при x = 0, а вторая (контур питания) – при x = L. Поэтому необходимо поставит по одному граничному условию на каждой границе. На контуре питания ставится условие постоянства давления или условие непроницаемости границы:

p(L, t) = pk или ux(L, t) = 0.

(1.68)

Скорость фильтрации связана с градиентом давления, поэтому второе граничное условие записывается в виде:

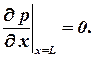(1.69)

На самой галерее ставится условие постоянства давления или задается расход, с которым работает галерея Q₀:

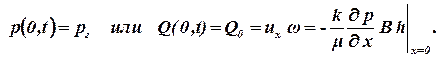(1.70)

Второе граничное условие можно записать в виде:

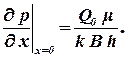(1.71)

Рассмотрим граничные условия в случае притока к скважине. В этом случае также имеются две границы: одна – на боковой поверхности скважины при r = r_c, а вторая – на контуре питания при r = R_k. На контуре питания ставится условие постоянства давления или условие непроницаемости границы:

p(Rk, t) = pk или ur(Rk, t) = 0.

(1.72)

Скорость фильтрации связана с градиентом давления, поэтому второе граничное условие записывается в виде:

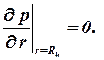(1.73)

На самой скважине ставится условие постоянство давления или задается расход Q₀, с которым она работает:

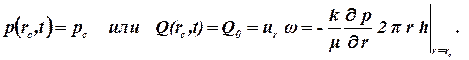(1.74)

Второе граничное условие можно записать в виде: