Двойственная задача линейного программирования и ее математическая модель
С каждой задачей ЛП связана другая задача. Название двойственной по отношению к исходной, заметим, что часто говорят о взаимодвойственных задачах т.к. если для исходной построена двойственная, а затем для неё так же построена двойственная, то получится исходная задача.
Рассмотрим пары взаимодвойственных задач позволяет решать ряд проблем:
1) Выбрать наиболее простой способ решения одной задачи, а из него найти решение другой задачи.
2) Рассматривая экономическую интерпретацию двойственных задач можно дать трактовку не только основным и дополнительным переменным, а ещё получить ряд дополнительных соотношений для прогноза и планирования, п и измененных условиях.
21. Виды двойственных задач. Правила составления симметричных двойственных задач линейного программирования.
Можно рассмотреть 2 вида двойственных задач:
- симметричный
- несимметричный
+ смешанный
Для симметричных двойственных задач характерно задание системы ограничений в виде системы неравенств.
Пусть прямая задача имеет вид:
F(x) = C1x1+C2X2+…+CnXn → max (в матрице после вертикальной границы вертикально стоят
Правило составления симметричной двойственной задачи ЛП.
1. каждому неравенству системы ограничений прямой задачи соответствует 1 переменная двойственной задачи Y=(y1, y2, …, ym) – вектор переменных двойственной задачи. Если в прямой задаче система ограничений содержит m строк, то в двойственной задаче будет m переменных.
2. коэффициенты системы ограничений двойственной задачи получаются путем транспонирования матрицы коэффициентов прямой задачи 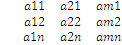 (здесь между 2 и 3 строчкой строка точек)
(здесь между 2 и 3 строчкой строка точек)
столбец свободных членов двойственной задачи состоит из коэффициентов целевой функции прямой задачи С1, С2, …, Сn.
3. коэффициентами целевой функции двойственной задачи служат элементы столбца свободных членов прямой задачи b1, b2, …,bm
4. знаки неравенств в системе ограничений двойственной задачи противоположны знакам неравенств прямой задачи (сохраняя при этом строгость)
5. экстремумы взаимодвойственных задач противоположны, т.е. если прямая задача на max, то двойственная на min. И наоборот.
6. для симметричных задач все переменные и прямой и двойственной задачи неотрицательны.
Таким образом, с учетом правил, симметричная двойственная задача примет вид
Z(Y)= b1y1+b2y2+…+bmym→min
a11y1+a21y2+…+am1ym≥c1
a12y2+a22y2+…+am2ym≥c2
………………………………
a1ny1+a2ny2+…+amnym≥cn
yi≥0, i=1,m
22. Виды двойственных задач. Правила составления несимметричных двойственных задач линейного программирования.
Можно рассмотреть 2 вида двойственных задач:
- симметричный
- несимметричный
+ смешанный
В несимметричном случае одна из задач представлена в канонической форме. (в матрице после вертикальной границы вертикально стоят y1,y2,…,ym)
!!! Основные правила составления двойственной задачи те же, что и в симметричном случае. Отличаются пункты 5 и 7.
5. Если в целевой функции двойственной задачи требуется найти max, то в системе ограничений будут содержаться неравенства вида ≤. А если двойственная задача на min, то ≥.
7. т.к. в прямой задаче в системе ограничений содержатся только уравнения, то в двойственной задаче условия неотрицательности отсутствуют. Т.е. yi – произвольно изменяющаяся переменная.
Таким образом для указанной прямой задачи двойственная задача примет вид:
Z(Y)= b1y1+b2y2+…+bmym→min
a11y1+a21y2+…+am1ym≥c1
a12y2+a22y2+…+am2ym≥c2
………………………………
a1ny1+a2ny2+…+amnym≥cn
yi≥0, i=1,m
23. Основное неравенство теории двойственности. Достаточный признак оптимальности. Первая теорема двойственности.
Основное неравенство теории двойственности: для любых допустимых решений пары взаимодвойственных задач X(x1, x2,…,xn), Y(y1,y2,…,ym) справедливо неравенство F(X)≤Z(Y)
Достаточный признак оптимальности:
если X*=(x*1,x*2,…,x*n) и Y*=(y*1,y*2,…,y*m) – допустимые решения задач, для которых выполняется условие F(X*)=Z(Y*), то X* и Y* - оптимальные решения двойственных задач!
Первая основная теорема двойственности:
если одна из взаимодвойственных задач имеет оптимальное решение, то другая задача также имеет оптимальное решение, причем для любых оптимальных решений X* и Y* выполняется равенство F(X*)=Z(Y*). Обратное утверждение тоже справедливо. Однако, если одна из двойственных задач не имеет решения вследствие ограниченности целевой функции F(X)→∞, то другая задача не будет иметь решения вследствие несовместности системы ограничений. Обратное утверждение не всегда верно, т.е. если задача имеет несовместную систему ограничений, то двойственная к ней может быть как неограниченной, так и ограниченной.
