Волны при наклонном падении на границу раздела сред

1. Предварительно определим вид уравнения плоской волны, распространяющейся в произвольном направлении относительно осей координат (рис. 3-49).

Пусть в момент начала наблюдения передний фронт плоской электромагнитной волны проходит через начало координат (положение 1). За время t волна доходит до положения (2), находящегося на расстоянии b от начала координат.

Введем единичный вектор n, перпендикулярный волновой поверхности. Комплексная амплитуда, например, напряженности электрического поля волны, распространяющегося в направлении n, выражается уравнением

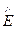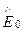= e^-gb, (1*)

где g = a + ik – постоянная распространения.

Модуль радиус-вектора b = bn, т.е. длина b, можно выразить через направляющие косинусы углов между вектором n и положительными направлениями осей координат. Если угол между осью x и n равен q, между осью y и n равен b, между осью z и n равен y, то

b = x cosq + y cos b+ z cos y = p x +m y +v z. (2*)

Направляющие косинусы. В декартовой системе координат радиус-вектор

b =xi+ yj + zk,

где i, j, k – орты в направлении, соответственно, осей x, y, z. Пусть углы между радиус-вектором b и осями x, y и z соответственно равны q, b, y. Проекции b на оси:

x = b cosq, y = b cosb, z = z cosy.

Косинусы cosq, cosb, cosy называются направляющими косинусами, определяющими направление вектора в выбранной системе координат.

Радиус-вектор теперь можно записать в виде:

b= (b cosq )i + (b cosb )j+ (b cosy )k.

Введем единичный радиус-вектор n, направленный так же, как и вектор b, т.е. у вектора n те же направляющие косинусы, что и у вектора b. Имеем:

n =1cosq i + 1 cosb j+ 1 cosy k.

Образуем скалярное произведение векторов bи n

bn =b = (xi+ yj + zk) (cosq i + cosb j+ cosy k) =

= x cosq + y cosb + z cosy . (3*)

Итак, модуль радиус-вектора bопределяется выражением

b = x cosq + y cosb + z cosy .

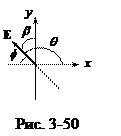Для краткости записи направляющие косинусы часто обозначаются буквами. Например, в выражении (2*) косинусы представлены буквами cosq = p, cosb = m, cosy = v, а модуль радиус-вектора bзаписан соответственно в виде b = p x +m y +v z.

В качестве иллюстрации сказанному приведем пример определения направляющих косинусов вектора E в плоскости x0y (см. рис. 3-50) в зависимости от заданных углов

p = cosq = - cosf = - sinb ; m = cosb = sin f = sina .

Уравнение для комплексной амплитуды (1*) запишем с учетом (2*):

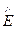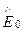= e^-gb = 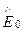e^{-g (x cosq + y cosb +z cosy)}. (4*)

В отсутствии затухания (a = 0 и g = a + ik = ik)

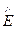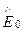= e^-ikb = 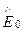e^{-i k (x cosq + y cosb +z cosy)} , (5*)

где: 1) волновой вектор k= kn определяет направление распространения волны (k = 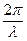- волновое число, l - длина волны).

Уравнение (4*) определят напряженность поля в любой точке волновой поверхности. Действительно, для любой точки волновой поверхности (2), определяемой радиус-вектором r, скалярное произведение nr=r cosj = b. Следовательно, kb = k r cosj =kr = knr , поэтому

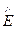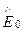= e^-ikb = 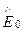e^-ikr= 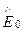e^-iknr= 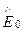e^{-i k (x cosq + y cosb +z cosy)}.

Так как скалярное произведениеkr = k_xx + k_yy + k_zz, то из последних соотношений получим:

k cosq = k_x; k cosb = k_y; k cosy = k_z. (6*)

2. Наклонное падение плоской электромагнитной волны на границу раздела сред (волна поляризована нормально к плоскости падения волны).

Рассмотрим ситуацию, когда вектор напряженности электрического поля волны Eперпендикулярен плоскости падения волны (рис. 51). Такая поляризация называется перпендикулярной или горизонтальной поляризацией. Плоскости падения волны - плоскости, образованные падающим лучом, отраженным лучом и нормалью, восставленной в точке падения луча. Плоскости падения на рис. 51 параллельны координатной плоскости Z0Y.

Запишем комплексные амплитуды векторов E и H падающей (вектор Пойнтинга П₁^/), отраженной (П₁^//) и преломленной (П₂) волн. Направление вектора Пойтинга перпендикулярно волновому фронту и соответствует направлению единичного вектора n, введенного впредыдущем пункте данного параграфа.

На рис. 51 q ^/ = q ^// =q - закон отражения. Ниже этот закон выведен из уравнений для вектора напряженности электрического поля

Из рис. 51 следует, что направляющие косинусы падающей волны П₁^/

p = 0; m = sinq ^/; v = - cosq ^/.

В соответствии с уравнением (4*), приведенным в пункте 1 данного параграфа, комплексные амплитуды падающей волны запишутся в виде

= ,

= .

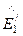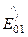
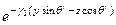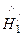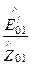
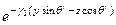Направляющие косинусы отраженной волны П₁^//

p = 0; m = sinq ^// ; v = cosq ^//.

Комплексные амплитуды отраженной волны

= , = .

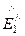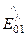
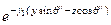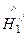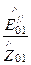
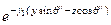Результирующее поле в первой среде равно сумме падающей и отраженной волн. Напряженность электрического поля в обеих средах имеет проекцию только по оси x (напряженность электрического поля в обеих средах параллельны плоскости раздела сред и имеют на границе сред только тангенциальную составляющую)

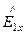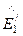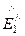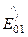
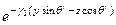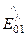
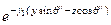= + = + . (130)

Напряженность магнитного поля имеет проекции по осям y и z (рис. 3-51):

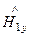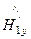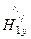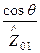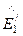
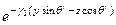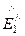
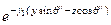= - = [ - ], (131)

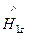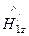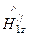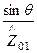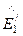
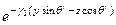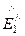
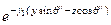= + = [ + ]. (132)

Во второй среде есть только преломленная волна. Направляющие косинусы преломленной волны П₂

p = 0; m = sinf ; v = - cosf.

Комплексные амплитуды преломленной волны

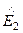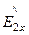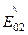
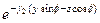= = , (133)

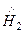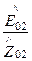
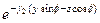= . (133*)

Магнитная составляющая 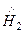также имеет проекции по осям y и z

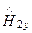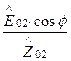
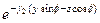= . (134)

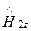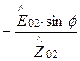
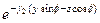= . (135)

На границе раздела сред тангенциальные (касательные) составляющие напряжения электрического и магнитного полей в первой и второй среде равны. В соответствии с граничным условием непрерывности тангенциальной составляющей имеем для электрического поля при z = 0 соотношение

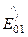
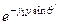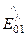
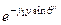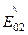
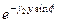+ = . (136)

Уравнение (136) должно выполняться при любых значениях координаты y на границе сред, т.е. во всех точках плоскости раздела сред. Например, при y = 0 получаем соотношение

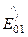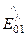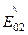+ = . (137)

От субъективного выбора положения начала координат граничное условие (136) не зависит, поэтому это уравнение возможно при выполнении условия

g₁sinq ^/ = g₁ sinq ^// = g₂ sinf. (138)

Из равенства (138) непосредственно следует:

1) закон отражения электромагнитной волны:

sinq ^/ = sin q ^// или q ^/ = q ^// =q , (139)

т.е. угол падения равен углу отражения и соответствующие вектора Пойнтинга П₁^/, П₁^// и нормаль в точке падения лежат в одной плоскости;

2) закон преломления

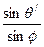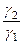= , (140)

Вектор Пойнтинга П₂ и нормаль в точке преломления лежат в одной плоскости

В частности, отсутствии затухания в средах (a₁ = a₂ = 0; g₁ = ik₁, g₁= ik₂) уравнение (136) примет вид:

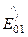
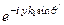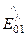
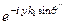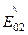
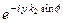+ = , (136*)

где k₁sinq 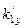^/ = , k₁ sinq 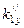^//= , k₂ sinf = 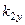- проекции волновых векторов соответственно падающей, отраженной и преломленной волн. Равенство (136*) выполняется при условии

k₁sinq ^/ = k₁ sinq ^// = k₂ sinf . (138*)

Из равенства (138*) следует:

1) закон отражения q ^/ = q ^// =q ;

2) закон отражения закон преломления в отсутствии затухания примет вид:

k₁sinq = k₂ sinf или 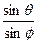= 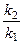, (140*)

Отношение волновых чисел 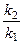= = 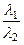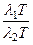, где T – период колебаний вектора напряженности электрического поля, поэтому

= ,

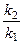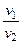где v₁ = 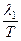- скорость электромагнитной волны в первой среде, v₂ = 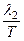- скорость электромагнитной волны во второй среде. Таким образом, закон преломления (140*) можно записать в виде

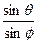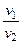= . (140**)

В случае, когда обе среды являются диэлектриками, имеем:

k₁ = 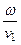= = 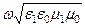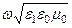, k₂ = = = .

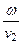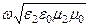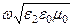Подставим эти соотношения в (140), получим закон преломления через отношение диэлектрических проницаемостей сред e₁ и e₂:

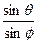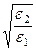= (140***)

В курсе общей физики при рассмотрении элементарной теории дисперсии показано, что показатель преломления среды связан с диэлектрической проницаемостью соотношением n = 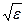. Следовательно, закон преломлении (140*) можно записать в виде 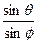= 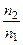. (140****)

Приведем без вывода формулы для коэффициентов отражения и пропускания в случае наклонного падения электромагнитной волны на границу сред:

- коэффициент отражения = ;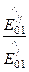

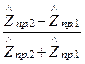- коэффициент пропускания (прозрачности) = .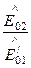

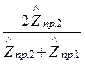В этих формулах 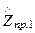= 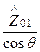, 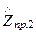= 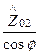- приведенные, соответственно, к углу падения и углу преломления волновые сопротивления сред. Таким образом, коэффициенты отражения и пропускания зависят от угла падения и угла преломления. Впрочем, т.к. угол преломления связан с углом падения по закону преломления, определяемый соотношением между диэлектрическими свойствами двух сред, то можно сказать, что коэффициенты 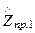и 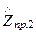зависят просто от угла падения.

Обратим внимание еще на одно обстоятельство. Запишем уравнения (130, 131, 132) при z = 0 с учетом закона отражения (139) q ^/ = q ^// =q :

= ( + ) ;

= ( + ) ;

= ( + ) .

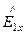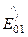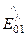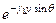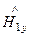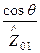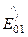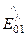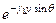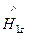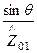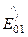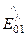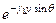Из этих уравнений следует, что вдоль поверхности раздела сред распространяется электромагнитная волна с постоянной распространения g₁sinq . Соответствующий вектор Пойнтинга образован векторами E_1x, и H_1z :

П = [E_1x, H_1z].

При вертикальной (параллельной) поляризации электрические и магнитные векторы в уравнениях меняются местами. Магнитный вектор при вертикальной поляризации имеет одну составляющую по оси x, а магнитный вектор две – по осям y и z.

3.8.3. Распространение плоской электромагнитной волны в

проводящей (поглощающей) среде при наклонном