Примеры отношения эквивалентности
Пример 1. Рассмотрим в качестве множества X множество натуральных чисел: 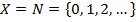 . Для него рассмотрим обычное равенство натуральных чисел. Скажем, что два натуральных числа эквивалентны, если они равны в обычном смысле. Очевидно, что это есть отношение эквивалентности.
. Для него рассмотрим обычное равенство натуральных чисел. Скажем, что два натуральных числа эквивалентны, если они равны в обычном смысле. Очевидно, что это есть отношение эквивалентности.
Пример 2. Рассмотрим произвольное натуральное число 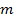 . Числа x и y назовем эквивалентными
. Числа x и y назовем эквивалентными 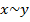 , если они дают один и тот же остаток при делении на
, если они дают один и тот же остаток при делении на 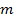 . Очевидно, что это есть отношение эквивалентности.
. Очевидно, что это есть отношение эквивалентности.
Пример 3. Введем отношение эквивалентности на множестве слов, длина которых не меньше числа 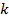 . Рассмотрим множество этих слов в алфавите
. Рассмотрим множество этих слов в алфавите 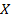 . Скажем, что пара слов
. Скажем, что пара слов 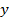 и
и  эквивалентны, если совпадают их первые
эквивалентны, если совпадают их первые 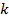 букв. Убедитесь сами, что все три свойства эквивалентности выполнены.
букв. Убедитесь сами, что все три свойства эквивалентности выполнены.
Утверждение. Пусть 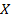 – множество,
– множество, 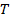 – отношение эквивалентности на нем. Тогда
– отношение эквивалентности на нем. Тогда 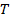 разбивает все элементы
разбивает все элементы 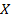 на классы эквивалентных элементов
на классы эквивалентных элементов  (Любая пара различных классов не пересекается между собой-
(Любая пара различных классов не пересекается между собой- 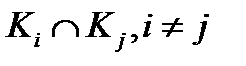 , и их объединение совпадает с множеством
, и их объединение совпадает с множеством 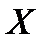 ;
;  ; количество классов может быть бесконечным). Любая пара элементов одного класса эквивалентна, а любая пара элементов различных классов не эквивалентна. Данное разбиение однозначно определяется отношением эквивалентности
; количество классов может быть бесконечным). Любая пара элементов одного класса эквивалентна, а любая пара элементов различных классов не эквивалентна. Данное разбиение однозначно определяется отношением эквивалентности 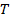 .
.
Доказательство данного утвнрждения предлагается в качестве самостоятельного упражнения.
Определение:суперпозицией булевых функции
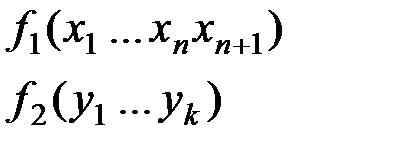
называется функция
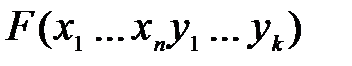 , полученная путем подстановки
, полученная путем подстановки
функции 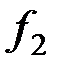 в функцию
в функцию 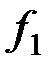 вместо некоторой переменной:
вместо некоторой переменной:  .
.
Замечание 1
Множества переменных подставляемых функций могут пересекаться.
Замечание 2
Переименование переменных есть частный случай суперпозиций : 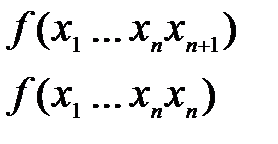 , в которой вместо
, в которой вместо 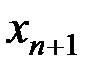 подставлена функция
подставлена функция 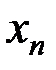 , то есть
, то есть 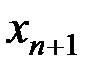 переименованна в
переименованна в 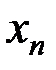 .
.
Определение
Будем различать переименование двух видов:
переименование с отождествлением, как в предыдущем примере (переменная переименуется в другую переменную этойже функции );
переименование без отождествления (когда переменная получает наименование, которого нет среди переменных функции).
Определение
Две функции назовем эквивалентными, если одну из другой можно получить переименованием переменных без отождествления.
Например эквивалентны 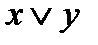 и
и 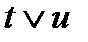 .
.
Функции 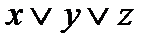 и
и 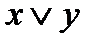 не эквивалентны, так как эквивалентные функции имеют одинаковое число существенных переменных.
не эквивалентны, так как эквивалентные функции имеют одинаковое число существенных переменных.
УтверждениеДвойственная суперпозиции функций- есть суперпозиция двойственных.
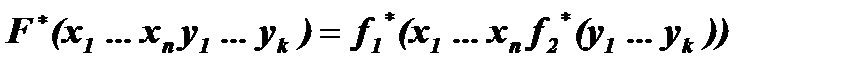
Доказательство
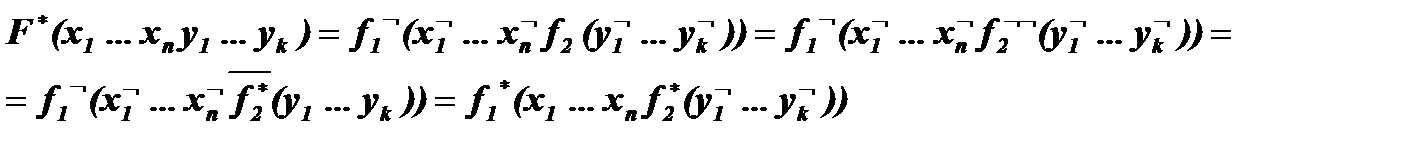
Тогда утверждение о представлении функции в виде СКНФнепосредственно следует из аналогичного утверждения о представлении функции в виде СДНФ.
