Ывод волнового уравнения для бегущих волн по струне.

1) Поперечные волны:

Пусть натяжение в струне Т. При малых деформациях изменением натяжения можно пренебречь. Пусть j(х) - угол между силой Т и горизонталью, p – линейная плотность струны.

dx T(x+dx)

j

T(x)

Из закона Ньютона для элемента (x,x+dx):

rdx¶²S/¶t²=T(sinj_x+dx - sinj_x )=T(tgj_x+dx – tgj_x)=T(j(x+dx)–j(x))=T 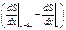, где r – линейная плотность, Þ 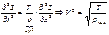, S(t,x)=S(t–(x/c)).

2) Продольные волны в твёрдом теле:

(рисунок)

e=dx’/dx, (e>0 – сжатие, e<0 – растяжение).

dm=srdx, (s – площадь), dm(¶²S/¶t²)=DF=F(x+Dx)–F(x)=Es 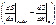Þ

msrdx(¶²S/¶t²)=Es 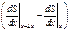Þ (¶²S/¶t²)=(E/r)(¶²S/¶x²) Þ c²=E/r

олновое уравнение для бегущих волн в газах. Скорость звука. Зависимость скорости звука от температуры.

олны в жидкости (газе).

Жидкости и газы обладают только объёмной упругостью. В них возможны только продольные волны.

Рассмотрим участок газа, сечения s, длины dx.

dm=r₀sdx; r₀sdx(¶²S/¶t²)=[P_x – P_x+dx]s; p₀(¶²S/¶t²)= – ¶P/¶x

P@p^g

При малых изменениях давления у положения p₀

dP = (¶P/¶r)_p0 dr =c²dr; –¶P/¶x =–c² ¶(dp/¶x)=–c² ¶/¶x[p₀(–¶S/¶x)]=c²p_o(¶²S/¶x²)

(¶²S/¶t²)= c² (¶²S/¶x²), c²= ¶P/¶r, при p=p₀

Зависимость от температуры:

P=rRT/M; P=const p^g; dP/dp= g const p^g-1= g P₀/r₀

Зависимость:C²=gP₀/r₀= g RT/M; g=C_P/C_V.

Билет № 24. Ничего не сделал.

Билет № 25.

Кинематика твердого тела

(Абсолютно) твердое тело – это система материальных точек, относительные положения которых остаются неизменными, то есть все макроскопические элементы такого тела неподвижны в системе координат жестко связанной с телом

Задача кинематики твердого тела – дать способы описания движения твердого тела и, исходя из закона его движения , определить положение , скорость и ускорение любой точки тела в любой момент времени.

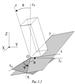Углы Эйлера

Число степеней свободы – это число независимых величин, которые необходимо задать для того, чтобы однозначно определить положение тела в пространстве.

Для того, что однозначно задать положение твердого тела в пространстве, надо зафиксировать три его точки, не лежащие на одной прямой. Одна материальная точка имеет три степени свободы (X,Y,Z). Две : 3+3-1=5 степеней. В этом случае координаты точек X₁,Y₁,Z₁ и X₂,Y₂,Z₂ не являются независимыми величинами, так как имеется уравнение связи L²=(X₂-X₁)²+(Y₂-Y₁)²+(Z₂-Z₁)² , Где L – расстояние между точками

Таким образом, в общем случае для твердого тела получаем 3+3+3-3=6 степеней свободы.

Зададим три различные декартовы системы координат:

1.Лабораторная X Y Z

2.Система X₀,Y₀,Z₀, начало которой связано с некоторой точкой О твердого тела, а оси остаются параллельными осям лабораторной системы X Y Z, т.е. она движется поступательно.

3.Система x y z, начало которой находится в той же точке О, что и начало x₀ y₀ z₀, а оси жестко связаны с твердым телом.

Тогда шести степеням свободы твердого тела будут соответствовать три координаты точки О (в X Y Z) и три угла φ, ψ, Θ, однозначно определяющие положение системы x y z относительно x₀ y₀ z₀ - углы Эйлера

φ – угол собственного вращения (поворот вокруг оси Z),

ψ – угол прецессии (поворот вокруг Z₀ с сохранением угла Θ между осями Z₀ и Z),

Θ – угол нутации (отклонение тела от оси Z₀)

Поступательное движение

Поступательное движение – это такое движение, при котором любой выделенный в теле отрезок остается параллельным самому себе (движение кабинок «колеса обозрения»).

Допустим, закон движения точки А задан в виде

Тогда закон движения точки В будет иметь вид

Где r_AB – вектор проведенный от точки А к точке В Скорость точки А V_A=dr_A/dt Скорость точки В V_B=dr_B/dt=V_A, т.к. r_AB=const Ускорение: a_A=dV_A/dt=dV_B/dt=a_B

Вращательное движениеВращательное движение – это такое, при котором две точки тела остаются все время неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки твердого тела, лежащие на оси вращения, неподвижны. Другие точки движутся по окружностям в плоскостях, перпендикулярных оси вращения.

Понятие угловая скорость и угловое ускорение относятся к случаю движения материальной точки по окружности. Положение точки М на окружности задается углом a, который составляет радиус-вектор точки М с неизменным направлением ОХ. Производная этого угла по времени называется угловой скоростью w: 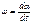. Если w = Сonst, то движение равномерно. n=w/2p – число оборотов в единицу времени (частота обращения).

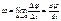Первая призводная угловой скорости и вторая производная угла по времени – это угловое ускорение: 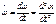. Продифференцируем S=r´a ь по времени и получаем: S’=(r’)*a+(a’)*r=w*r S’’=(w*r)’=r*w’+r’*w=re (тангенциальное ускорение)+v*w (=v²/r — центростремительное). Угловое перемещение всех точек твердого тела за одно и тоже время будут одинаковыми.

Угловая скорость:

Вектор элементарного углового перемещения Δφ направлен вдоль оси вращения в соответствии с правилом буравчика. Вектор угловой скорости ω=dφ/dt определяет модуль угловой скорости, ориентацию оси вращения в пространстве и направление вращения тела. Вектор скорости V_A: V_A=ω×r_A(формула Эйлера) V_A=ω r_A*sinα=ωρ Ускорение точки А:

a_A=d ω/dt×r_A+ω×dr_A/dt=ε×r_A+ω×V_A

e -угловое ускорение тела

a_A=a_t+a_n - все три вектора лежат в плоскости, перпендикулярной оси вращения a_t=e×r_A=e*ρ*t - тангенциальное ускорение (t - единичный вектор в направлении V_A).

a_n=ω× V_A=ω×(ω×r_A)=ω²rn – центростремительное ускорение (n – единичный вектор в направлении к оси вращения)

Плоское движение

Плоское движение – это такое движение твердого тела, при котором траектории всех его точек лежат в неподвижных параллельных плоскостях.

Скорость любой точки А тела геометрически складывается из скорости какой-либо другой точки О, принятой за полюс, и скорости вращательного движения вокруг этого полюса.

Радиус-вектор точки А:

r_A=r₀+r` ,r` - вектор, проведенный из полюса в точку А.

Скорость точки А:

V_A= dr_A/dt= dr₀/dt+ dr`/dt=V<sub>0</sub>+ω×r`

Отсюда можно сделать вывод, что в любой момент времени должна существовать такая точка М, скорость которой в лабораторной системе X Y Z равна нулю – для этой точки

V₀= -ω×r`

Причем точка может находиться и вне тела.

Таким образом, плоское движение твердого тела в данный момент времени можно представить как чистое вращение вокруг оси, проходящей через эту точку М - мгновенной оси вращения.

Ускорение точки А:

a_A=dV_A/dt=dV₀/dt+dω/dt×r`+ω× dr`/dt=a₀+a_t+a_n

a_t=e×r` a<sub>n</sub>=ω× dr`/dt=ω×(ω×r`)=ω*(ω*r`)-r`(ω*ω)=-ω<sup>2</sup>*r`

((ω*r`)=0, т.к. ω^r`)

Мгновенная ось – ось с помощью которой можно представить движение тела, как чистое вращение. (Как поле брани усеяно белыми костми, так и дорога мгновенными осьми)

Пункт 2. При наложении распространяющихся навстречу монохроматических волн одинаковой частоты, амплитуды (например, прямой и отражённой) образуются стоячие волны.

s(t,x)=Acos[w (t–x/c)]–Acos[w (t+x/c)]=2Asin[w x/c]sinw t

В каждой точке порисходит гармоническое колебание с частотой w, причём амплитуда зависит от положения точки по закону: А(х)=2А|sin[wx/c]|

Билет № 26.

Твердое тело может рассматриваться как система материальных точек, расстояние между которыми постоянно.Поэтому все уравнения справедливые для системы материальных точек справедливы и для твердого тела: dp/dt=F; dL/dt=M; Для твёрдого тела эти уравнения являются замкнутой системой с их помощью без каких либо дополнительных условий можно полностью определить движение твёрдого тела в заданых внешних силовых полях. Необходимо лишь знать начальные условия. Из кинематики плоского движения известно, что в этом случае все точки движутся в пврвллельных плоскостях . Поэтому достаточно рассмотретьь движение какого-либо сечения тела в одной плоскости. Вектор угловой скорости всегда перпендикулярен плоскоски и следовательно имеет постоянное направление. Поэтому если ось Z связанной с телом системы провести перпендикулярно плоскости движения, то угловая скороть вращения всегда будет направленна по этой оси. Для того чтобы избежать учёта центробежных моментов тензора инерции целесообразно ось вращения провести через центр масс. Таким образом уравнения для плоского движения примут вид: mdv/dt=F; Jdw/dt=M;

Уравнение моментов. Момент инерции относительно закрепленной оси. Рассмотрим твердое тело как систему жестко связанных между собой материальных точек. Уравнение движения для i-й материальной точки массы m, в лабораторной системе координат имеет вид:

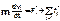
где F. — сумма всех внешних сил, действующих на i-ю материальную точку, f — сила, действующая на i-ю материальную точку со стороны j-й материальной точки, т.е. внутренняя сила. Будем полагать, что силы взаимодействия являются центральными, то есть векторы 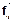и 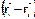коллинеарны.

Умножим обе части уравнения движения (В.6) векторно на радиус-век­тор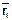

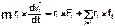
С учетом того, что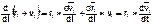

(так kак 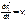,то 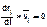), после суммирования по всем точкам системы получим

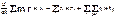
Величина 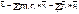^— импульс i-й материаль-

ной точки) называется моментом импульса системы относительно некото­рой неподвижной точки, выбранной за начало координат;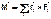

момент внешних сил относительно той же точки; величина 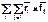является моментом всех внутренних сил. Выражение для момента внутренних сил можно преобразовать:

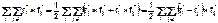
Заметим, что для центральных сил 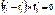. Тогда с

учетом введенных выше обозначений уравнение (В.8) записывается в следующем виде:

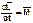(B10)

Это уравнение называется уравнением моментов.