Муниципальное образовательное учреждение
Вопросы и задачи контрольной работы
1. Биография Александра Михайловича Ляпунова.
2. Биография Владимира Игоревича Арнольда.
3. Биография Карла Теодора Вильгельма Вейерштрасса.
4. Биография Франсуа Виета.
5. Биография Иоганна Карла Фридриха Гаусса.
6. Биография Рене Декарта.
7. Биография Жюля Анри Пуанкаре.
8. Биография Софьи Васильевны Ковалевской.
9. Биография Андрея Николаевича Колмогорова.
10. Биография Николая Ивановича Лобачевского.
11. Определение предела числовой последовательности. Теорема об единственности предела последовательности. Теоремы о предельном переходе в неравенствах.
12. Теорема об ограниченности сходящейся последовательности. Бесконечно малая последовательность. Арифметические операции над бесконечно малыми последовательностями. Арифметические операции над сходящимися последовательностями: предел суммы, произведения, частного последовательностей.
13. Односторонние пределы. Бесконечно малые величины, их свойства. Бесконечно большие величины, их свойства.
14. Предел и его свойства. Точки разрыва функции. Первый и второй замечательные пределы.
15. Односторонние пределы. Непрерывность функции в точке. Бесконечно малые. Сравнение порядка бесконечно малых. Первый и второй замечательные пределы.
16. Асимптоты. Точки разрыва функции.
17. Бесконечно малые функции при х → а и их свойства. Бесконечно большие функции при х → ∞
18. Предел функции в точке и его свойства. Предел функции при х → ∞ и его свойства. Предел функции при х →+∞ и его свойства.
19. Понятие производной, геометрический смысл. Производные основных элементарных функций. Таблица производных. Основные правила дифференцирования.
20. Сложная функция. Теорема о производной сложной функции. Производная степенной, показательной и степенно-показательной функции.
21. Обратная функция. Теорема о производной обратной функции. Производные обратных тригонометрических функций.
22. Дифференциал функции, его геометрический смысл.
23. Производная функции, заданной параметрически. Производные и дифференциалы высших порядков.
24. Первообразная. Неопределенный интеграл. Определение. Таблица интегралов. Свойства неопределенных интегралов.
25. Способы интегрирования. Замена переменных. Способы интегрирования функций, содержащих квадратный трехчлен.
26. Интегрирование по частям.
27. Правильные и неправильные рациональные дроби. Интегралы от рациональных дробей.
28. Интегралы от иррациональных функций.
29. Интегралы от тригонометрических функций. Универсальная подстановка.
30. Функции, интегралы от которых не выражаются через элементарные функции.
31. Эллиптический интеграл. Интегральный синус, косинус, логарифм.
32. Определенный интеграл. Существование. Нижняя и верхняя интегральные суммы. Равномерная непрерывность функции.
33. Шесть свойств определенного интеграла, включая теорему о среднем.
34. Формула Ньютона-Лейбница.
35. Несобственные интегралы. Сходимость и абсолютная сходимость. Интеграл от разрывной функции.
36. Приложение определенного интеграла. Площадь плоской фигуры в декартовой и полярной системе координат.
37. Эллипс инерции. Неравенство Буняковского. Определение, история появления
38. Формула Грина. Определение, история появления
39. Формула Остроградского. Определение, история появления
40. Дискретная математика.
41. Множества, собственное подмножество. Объединение множеств, пересечение, разность, симметрическая разность, абсолютное дополнением. Универсальное множество. Свойства операций (коммутативность, ассоциативность, дистрибутивность, идемпотентность).
42. Свойства универсального и пустого множеств. Закон двойного дополнения. Законы де Моргана. Парадокс Рассела. Булеан. Мощность множества. Мощность булеана.
43. Прямое произведение. Упорядоченная пара. Три свойства прямого произведения. Соответствие между множествами.
44. Отношения унарные и бинарные. Граф отношения. Матрица отношения. Единичное отношение. Полное отношение. Обратное отношение. Свойства отношений (рефлексивность, антирефлексивность, симметричность, антисимметричность, асимметричность, транзитивность).
45. Предмет теории вероятностей. Применение теории вероятностей в экономических исследованиях.
46. Случайные события. Сумма, произведение случайных событий. Противоположные случайные события.
47. Основные формулы комбинаторики. Классическое определение вероятности.
48. Вероятность суммы конечного числа несовместимых событий. Вероятность противоположного события.
49. Вероятность произведения событий. Вероятность произведения независимых событий и событий независимых в совокупности.
50. Ограниченные множества. Верхняя и нижняя граница множества. Точная верхняя и точная нижняя граница множества. Теорема о существовании точной верхней и точной нижней границы множества.
51. Найдите наименьшее значение функции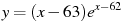 
на отрезке 
.
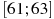52. Найдите наибольшее значение функции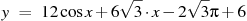 
на отрезке 
.
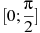53. Найдите наименьшее значение функции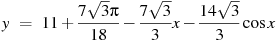 
на отрезке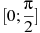
54. Найдите наименьшее значение функции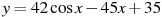 
на отрезке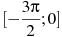 
55. Найдите наибольшее значение функции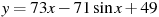 
на отрезке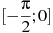 
56. Найдите наименьшее значение функции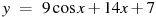 
на отрезке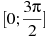 
57. Найдите наименьшее значение функции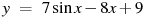 
на отрезке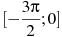
58. Найдите наименьшее значение функции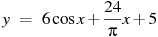 
на отрезке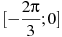 
59. Найдите наибольшее значение функции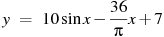 
на отрезке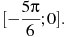 
60. Найдите наибольшее значение функции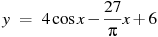 
на отрезке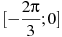
61. Решите уравнение
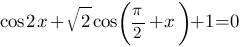
Укажите корни этого уравнения, принадлежащие отрезку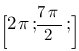 
62. Решите уравнение
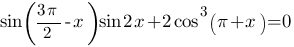
Укажите корни этого уравнения, принадлежащие отрезку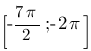 
63. Решите уравнение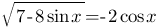 
Укажите корни этого уравнения, принадлежащие отрезку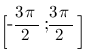 
64. Решите уравнение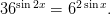 
Укажите все корни этого уравнения, принадлежащие отрезку
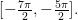
65. Решите уравнение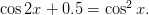 
Укажите все корни этого уравнения, принадлежащие отрезку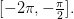 
66 – 80. Вычислить пределы функций.
66. 
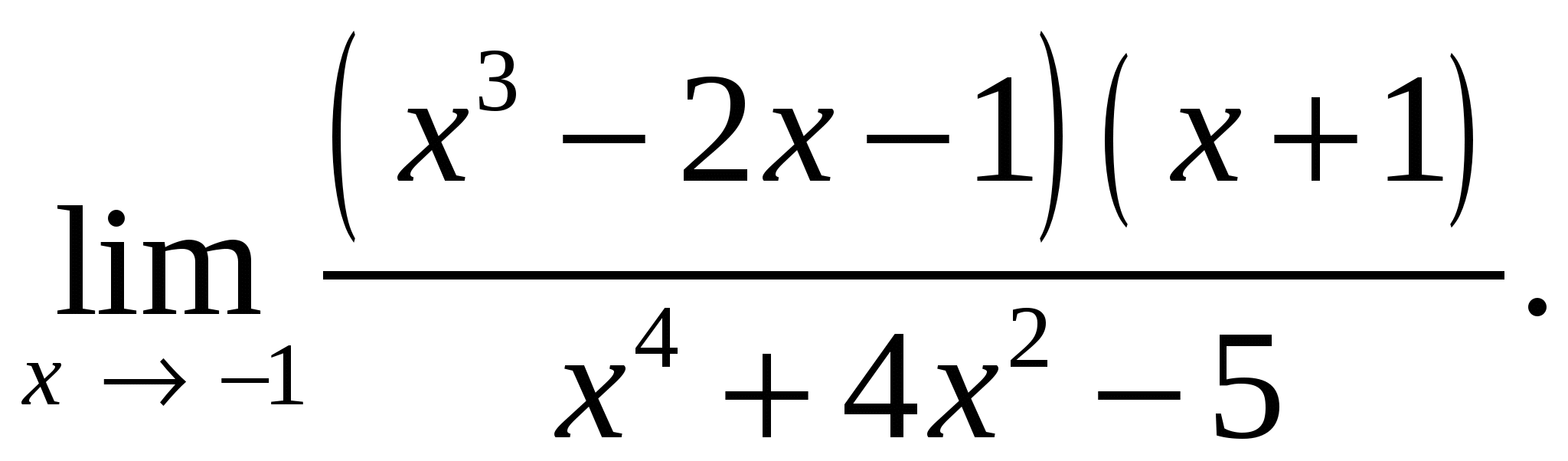
67. 
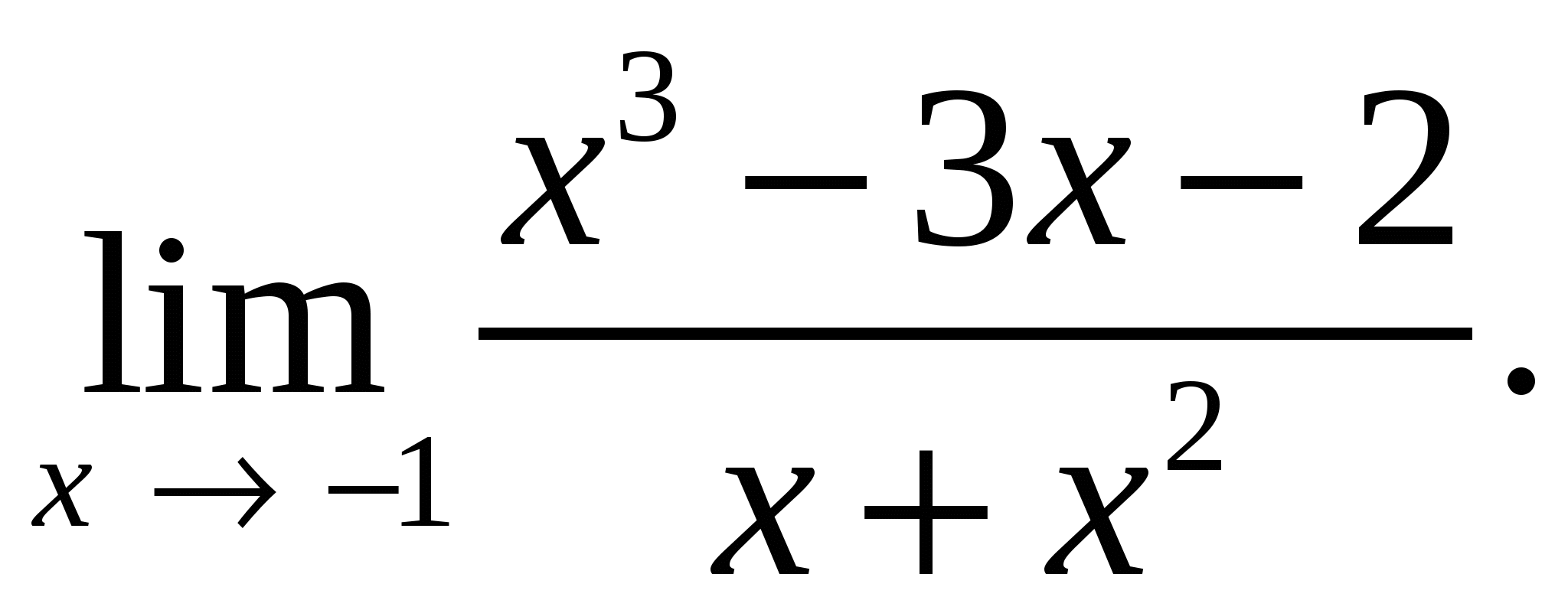
68. 
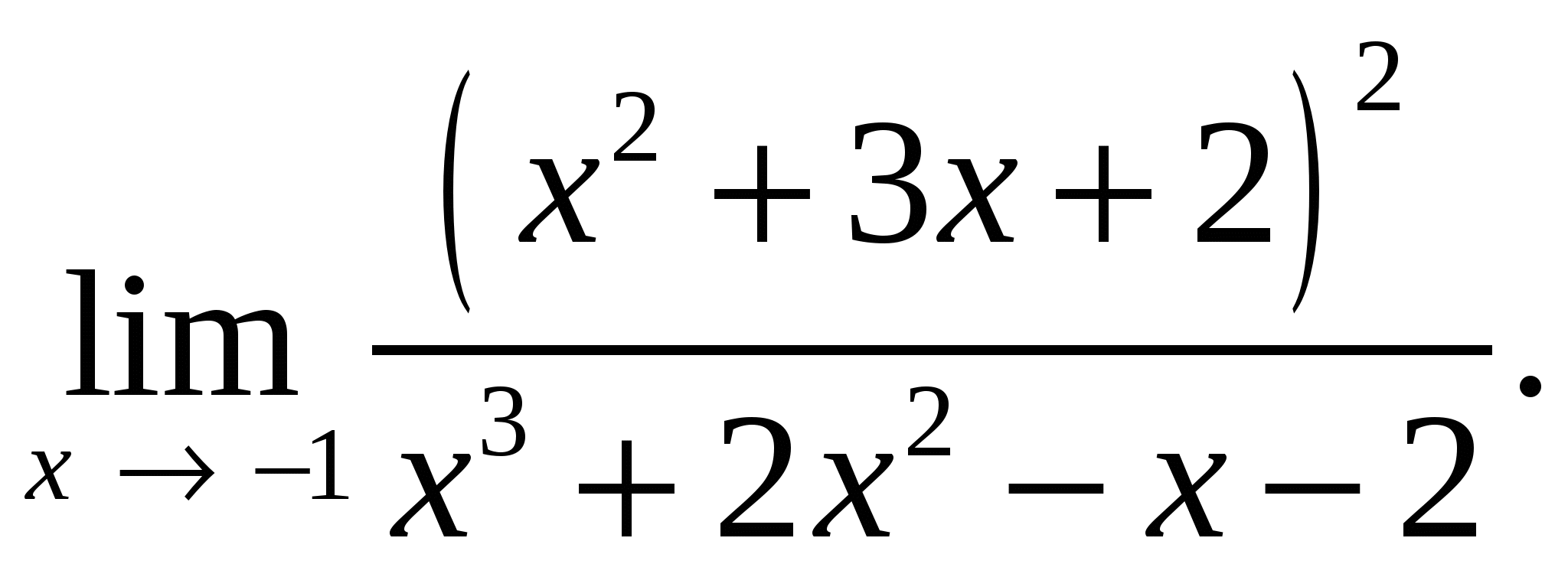
69. 
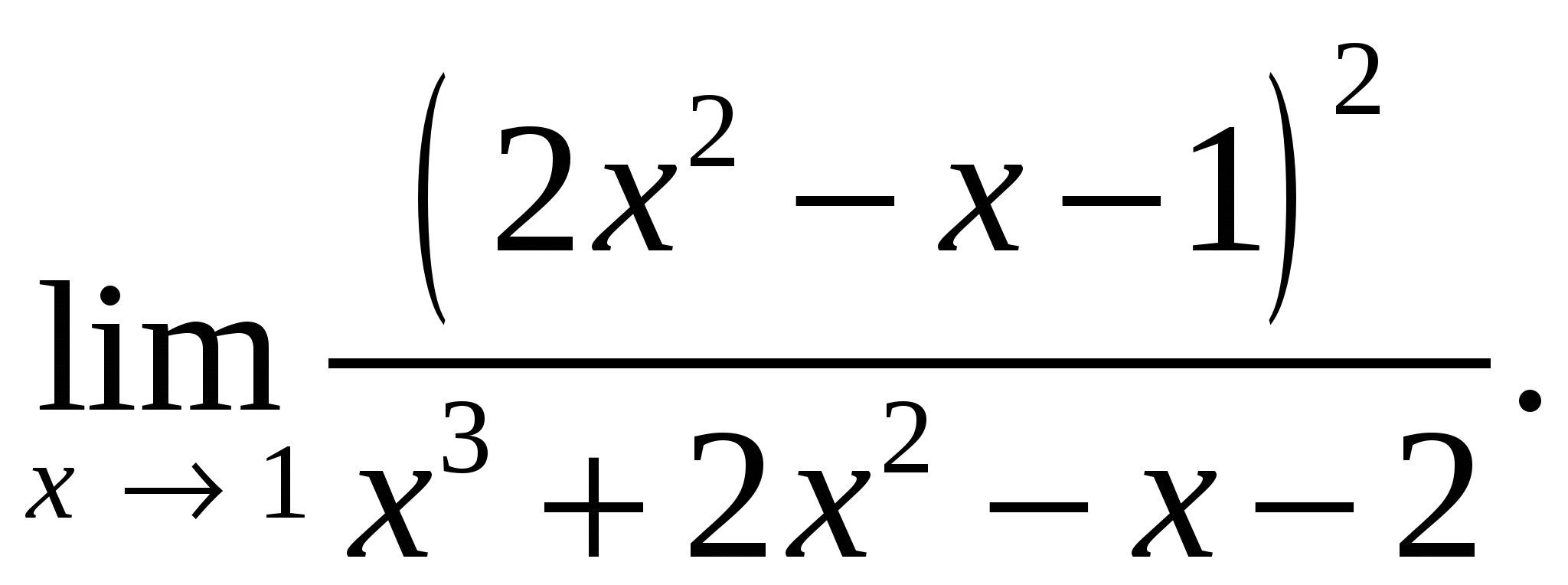
70. 
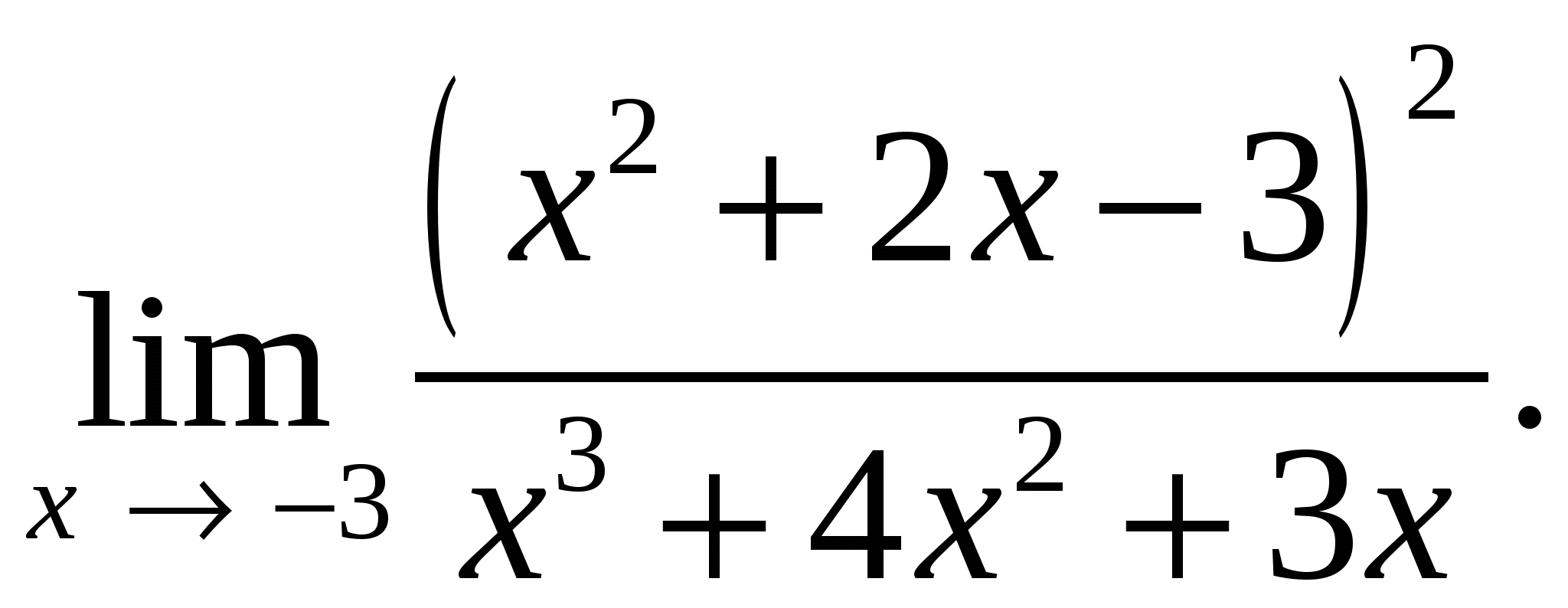
71. 
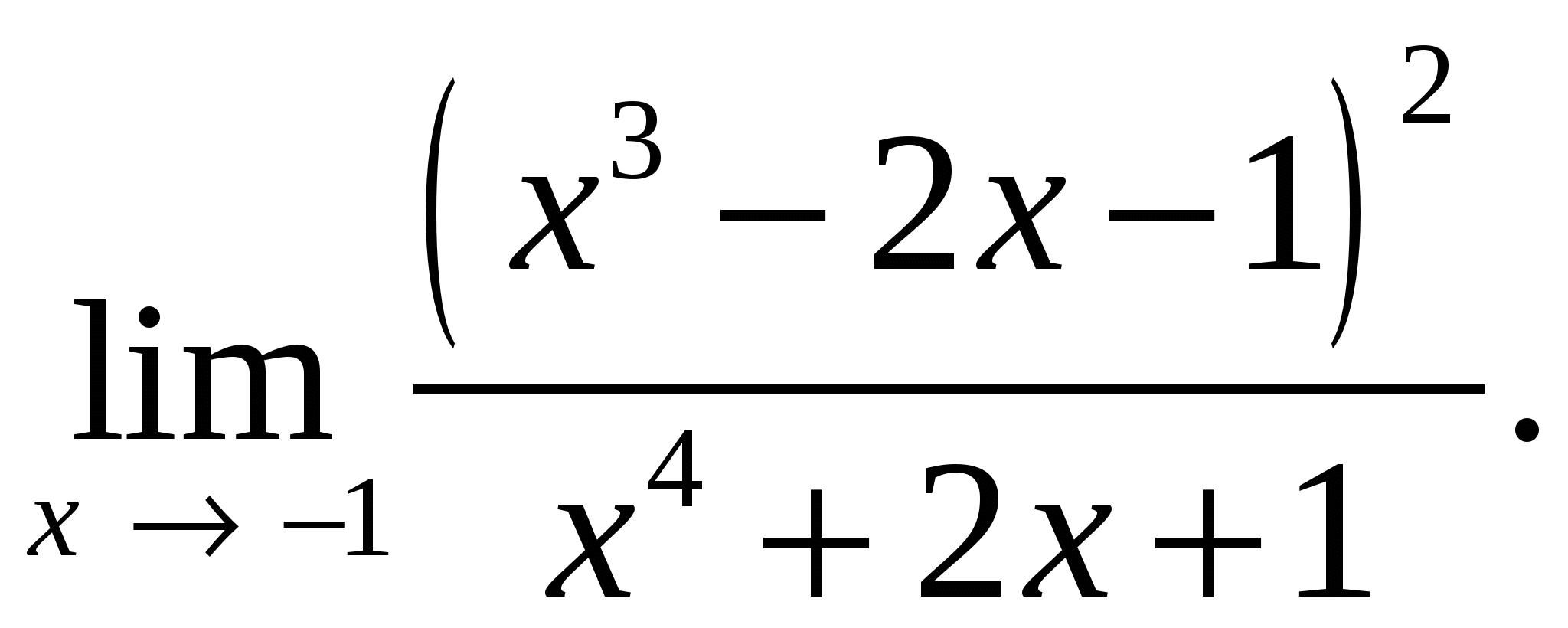
72. 
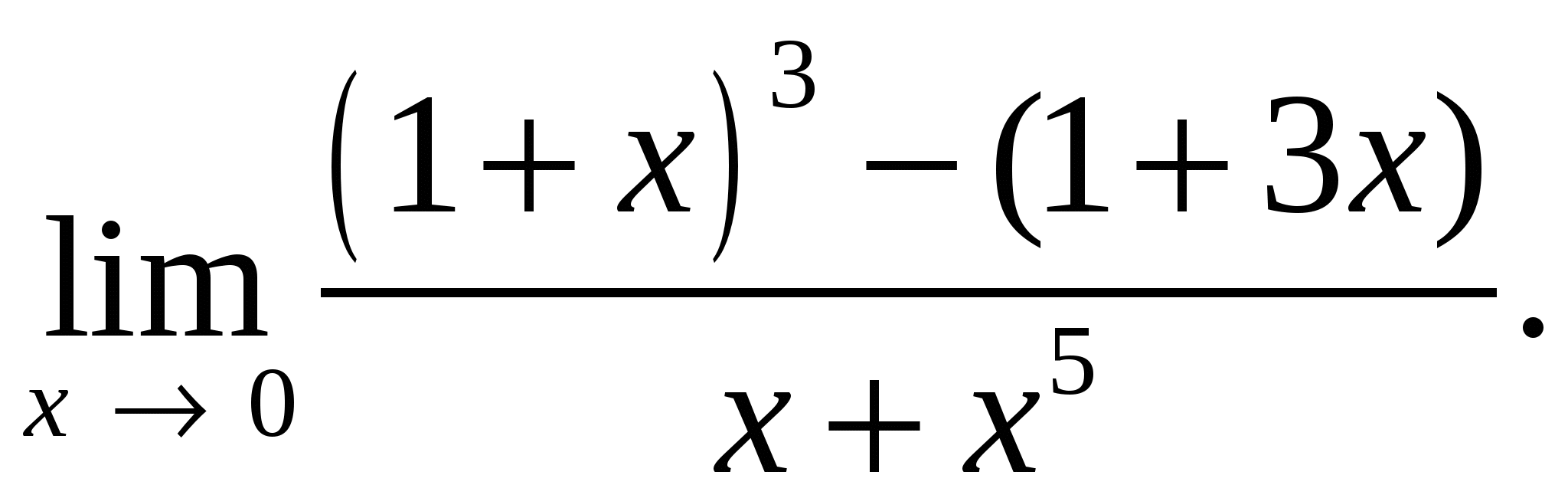
73. 
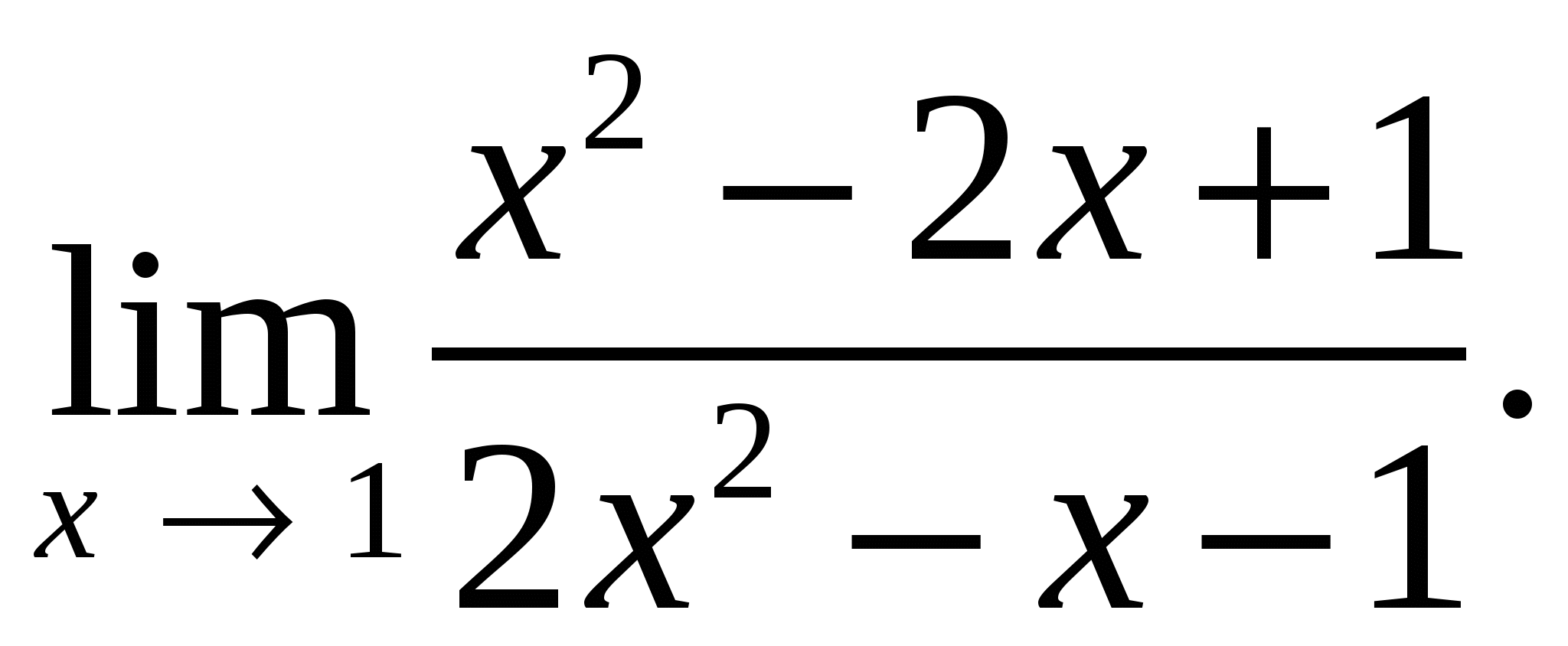
74. 
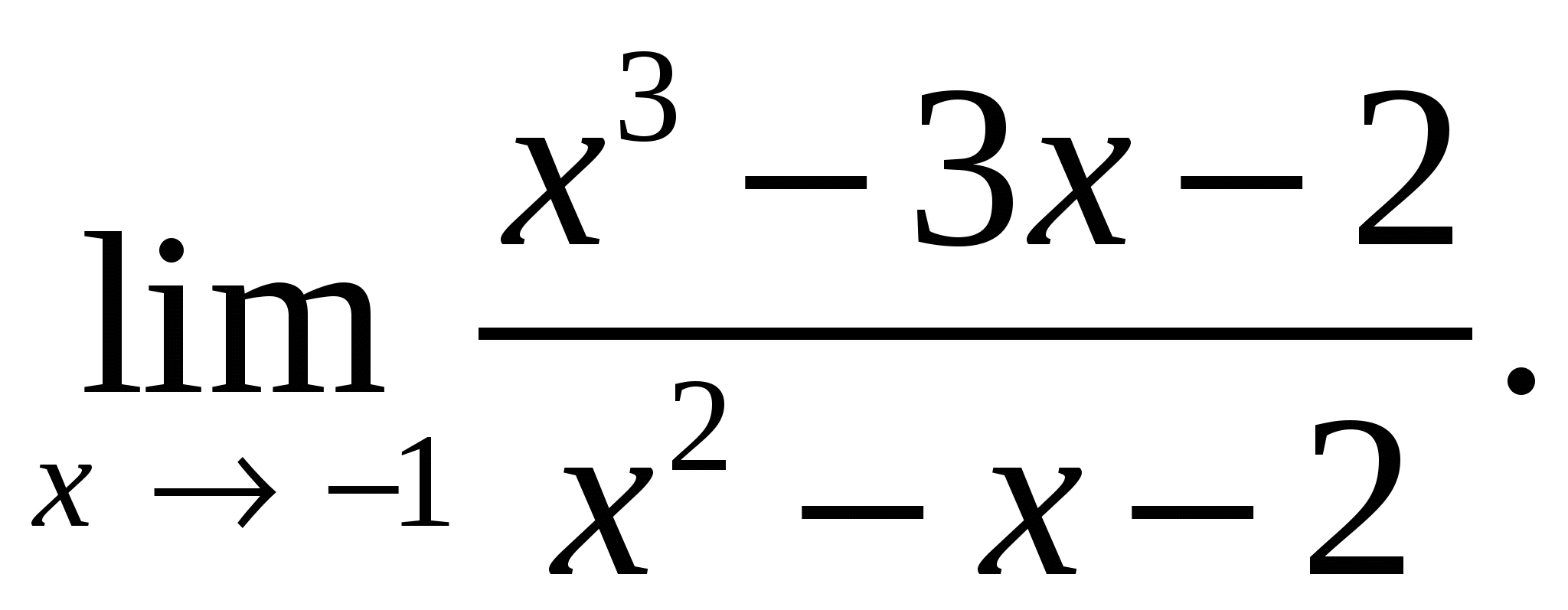
75. 
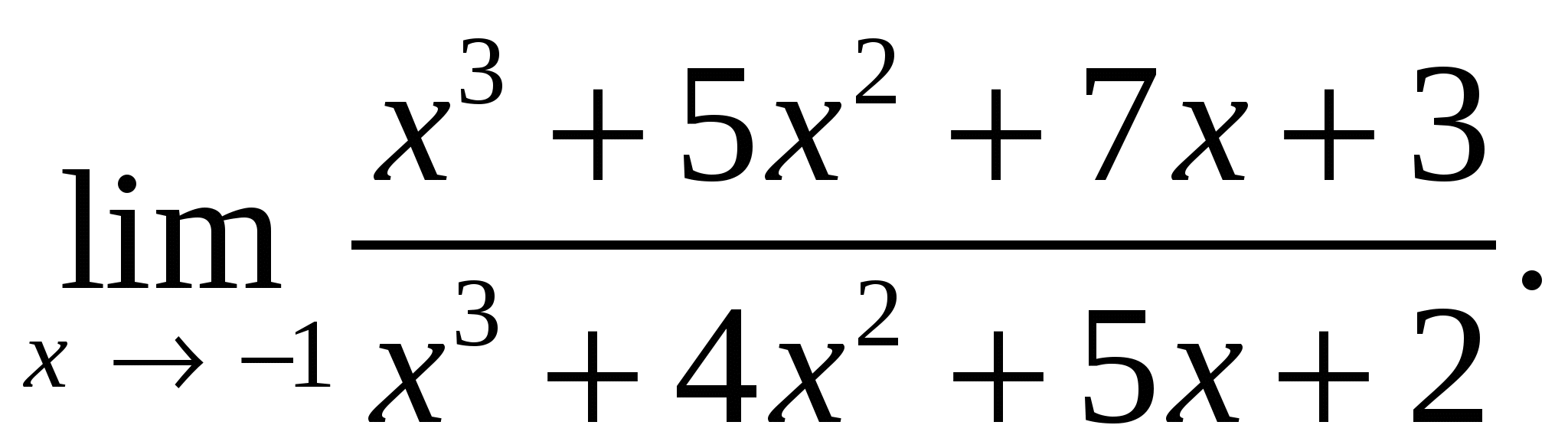
76. 
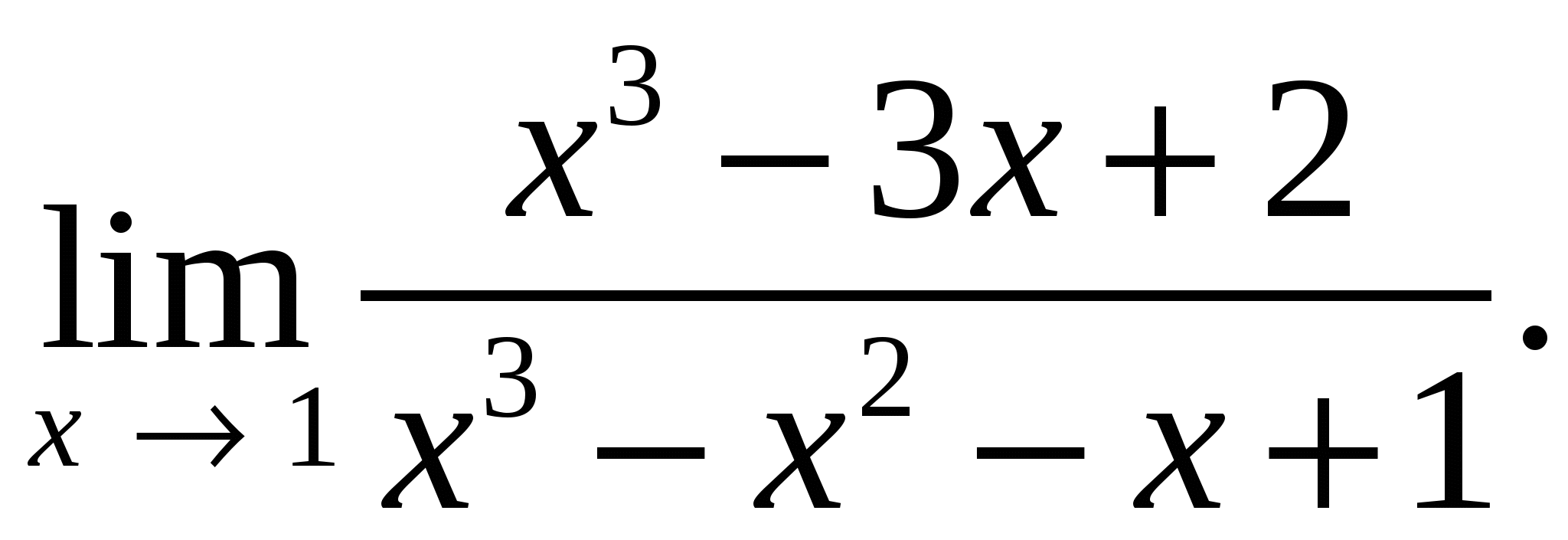
77. 
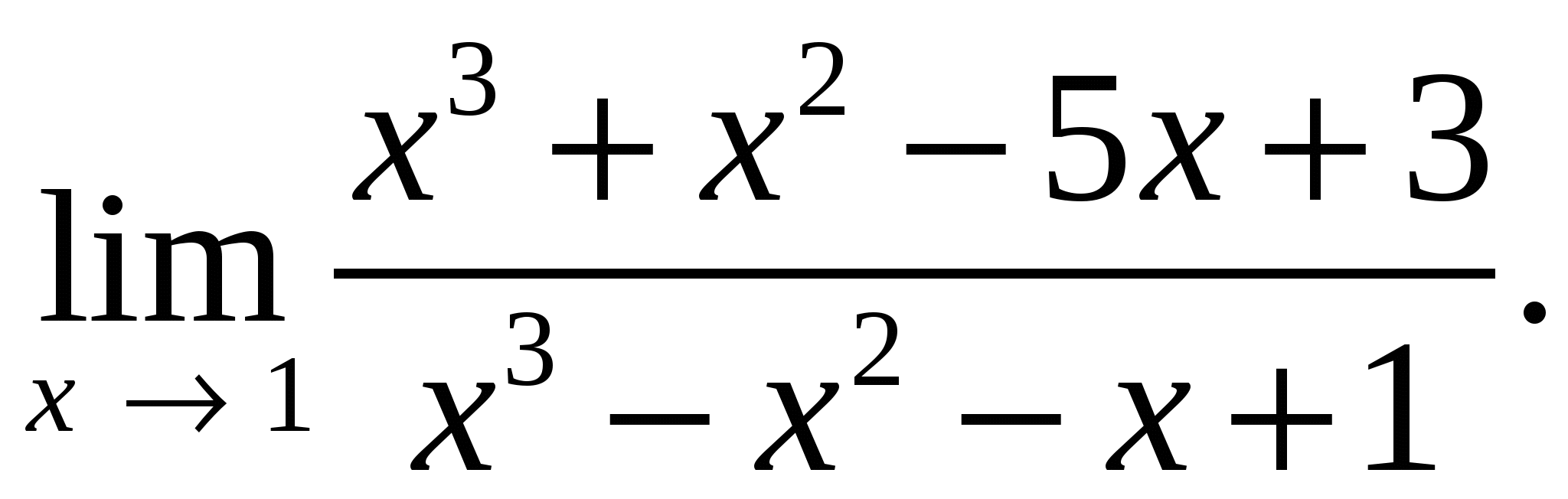
78. 
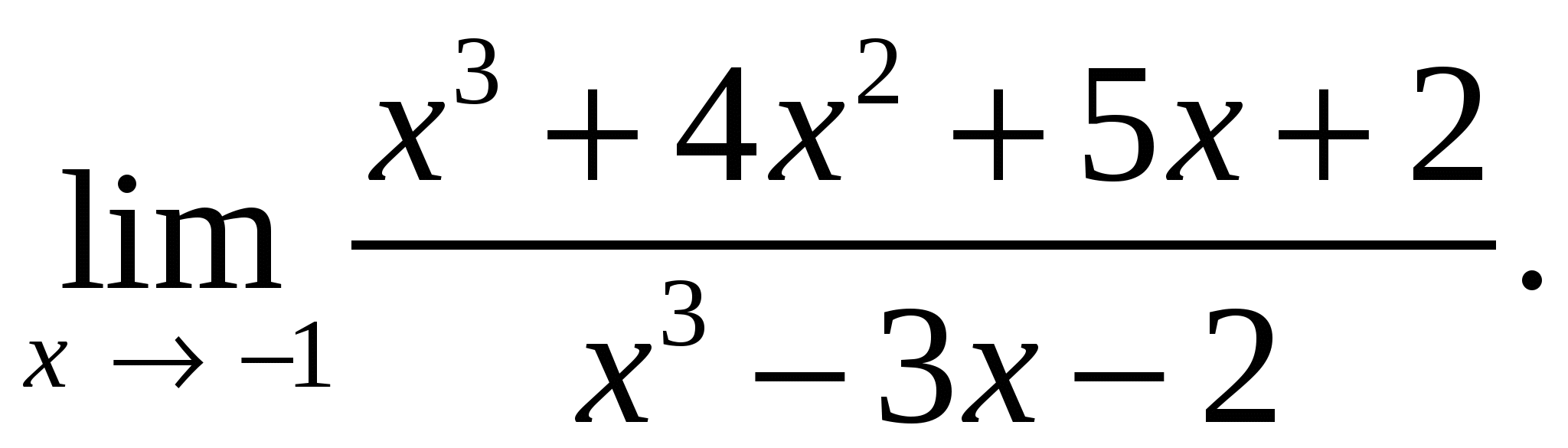
79. 
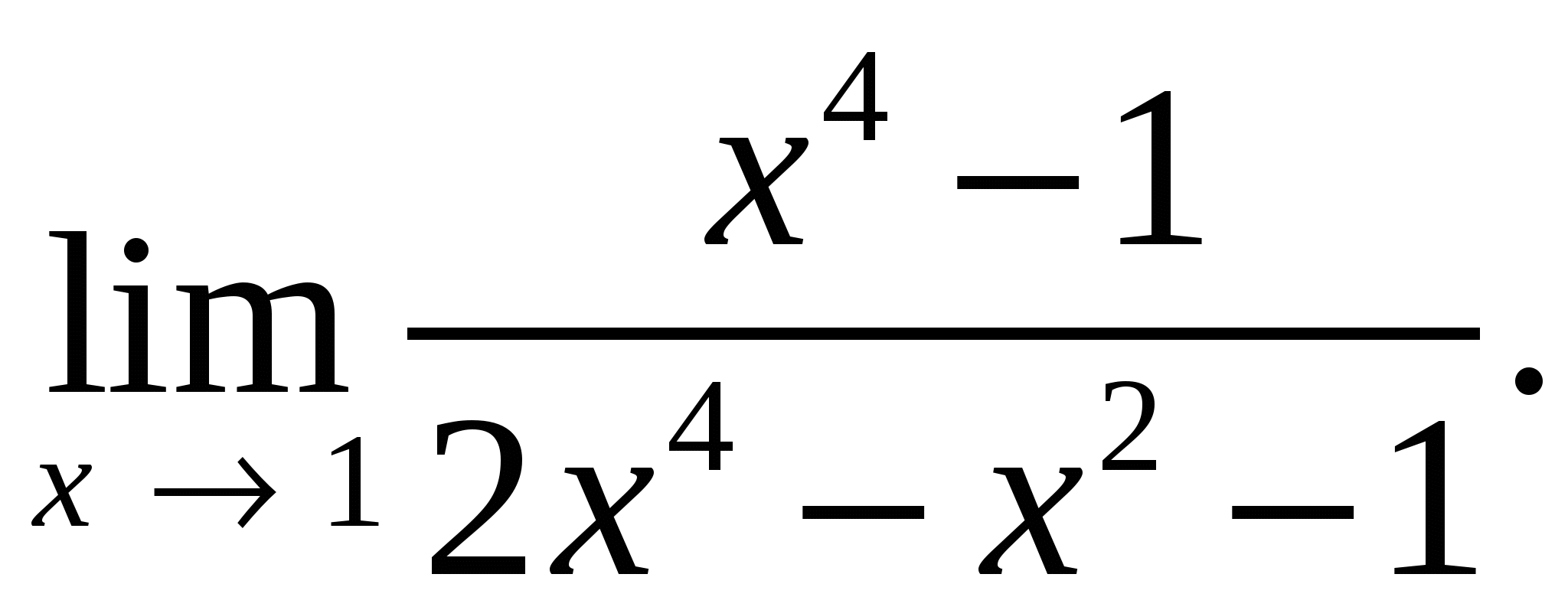
80. 
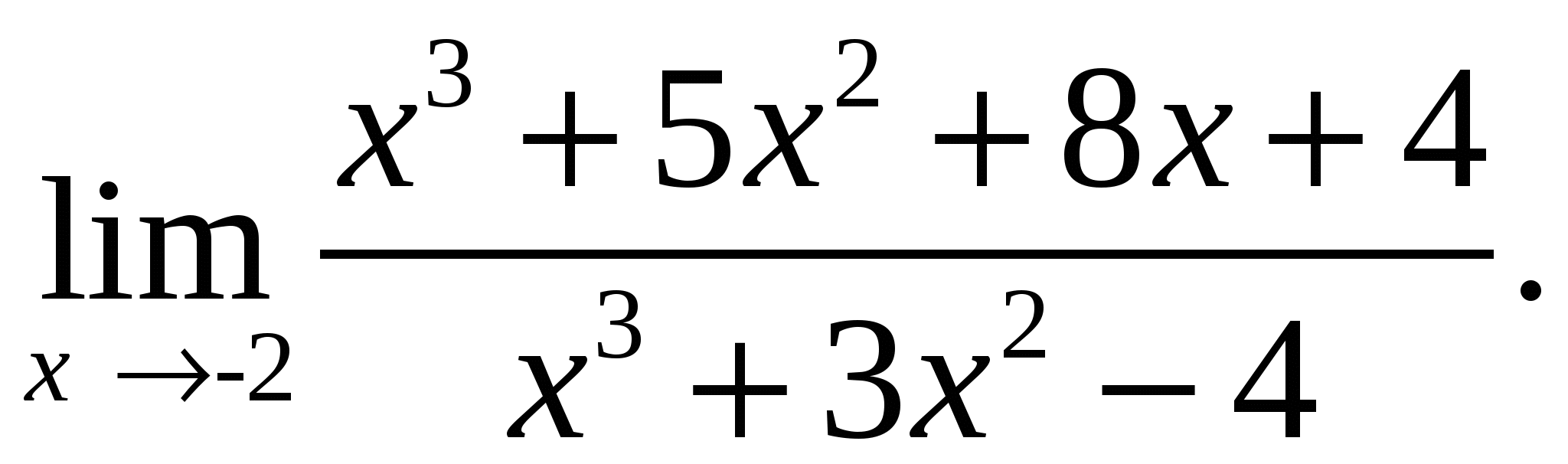
81 – 90. Найти производные функций
81. 
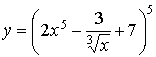
82. 
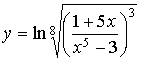
83. 
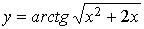
84. 
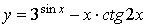
85. 
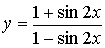
86. 
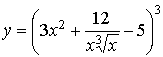
87. 
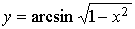
88.
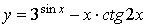
89. 
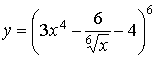
90. 
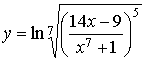
91 – 100. Найдите интегралы:
91. 
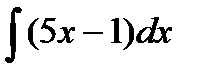
92. 
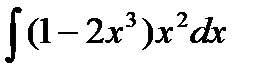
93. 
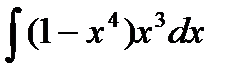
94. 
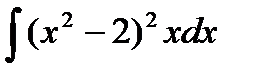
95. 
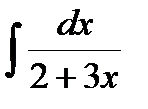
96. 
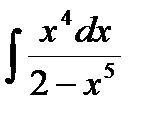
97. 
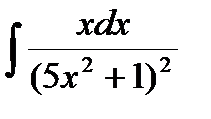
98. 
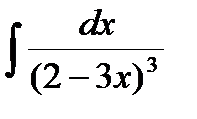
99. 
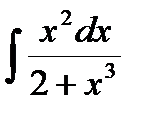
100. 
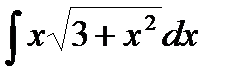
101 – 110. Вычислите определение интегралы:
101. 
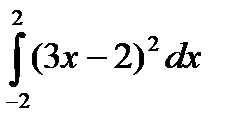
102. 
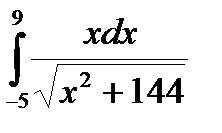
103. 
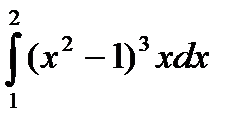
104. 
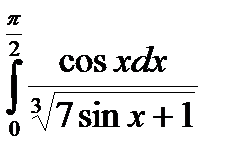
105. 
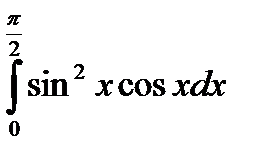
106. 
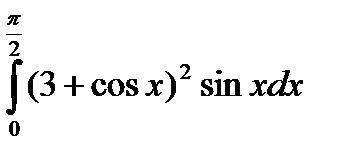
107. 
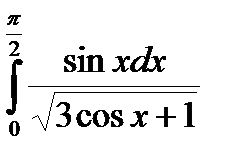
108. 
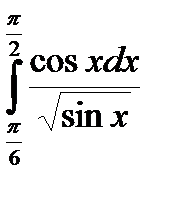
109. 
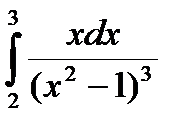
110. 
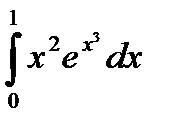
Приложение 1
МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ОБРАЗОВАНИЯ