Задачи для 1-го практического занятия

Е практическое занятие

Определение количественных характеристик надежности

По статистическим данным об отказах изделия

Теоретические сведения

Вероятность безотказной работы по статистическим данным об отказах оценивается выражением

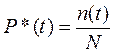, (1.1)

где n(t) - число изделий, не отказавших к моменту времени t; N- число изделий, поставленных на испытания; Р*(t) - статистическая оценка вероятности безотказной работы изделия.

Для вероятности отказа по статистическим данным справедливо соотношение

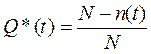, (1.2)

где N-n(t) – число изделий, отказавших к моменту времени t; Q*(t) – статистическая оценка вероятности отказа изделия.

Частота отказов по статистическим данным об отказах определяется выражением

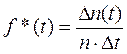, (1.3)

где Δn(t) – число отказавших изделий на участке времени (t, t+Δt); f*(t) – статистическая оценка частоты отказов изделия; Δt – интервал времени.

Интенсивность отказов по статистическим данным об отказах определяется формулой

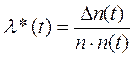, (1.4)

где n(t) – число изделий, не отказавших к моменту времени t; Δn(t) – число отказавших изделий на участке времени (t, t+Δt); λ*(t) – статистическая оценка интенсивности отказов изделия.

Среднее время безотказной работы изделия по статистическим данным оценивается выражением

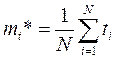, (1.5)

где t_i – время безотказной работы i-го изделия; N – общее число изделий, поставленных на испытания; m_t* – статистическая оценка среднего времени безотказной работы изделия.

Для определения m_t* по формуле (1.5) необходимо знать моменты выхода из строя всех N изделий. Можно определять m_t* из уравнения

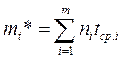, (1.6)

где n_i – количество вышедших из строя изделий в i-ом интервале времени; t_ср.i = (t_i-1+t_i)/2 ; m = t_k/Δt ; Δt = t_i+1-t_i; t_i-1 – время начала i-го интервала; t_i – время конца i-го интервала; t_k – время, в течение которого вышли из строя все изделия; Δt – интервал времени.

Дисперсия времени безотказной работы изделия по статистическим данным определяется формулой

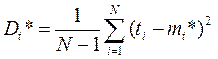, (1.7)

где D_t* – статистическая оценка дисперсии времени безотказной работы изделия.

Задачи для 1-го практического занятия

Задача 1.1. На испытание поставлено 1000 однотипных электронных ламп, за 3000 час. отказало 80 ламп. Требуется определить P*(t), q*(t) при t = 3000 час.

Задача 1.2. На испытание было поставлено 1000 однотипных ламп. За первые 3000 час. отказало 80 ламп, а за интервал времени 3000 - 4000 час. отказало еще 50 ламп. Требуется определить статистическую оценку частоты и интенсивности отказов электронных ламп в промежутке времени 3000 - 4000 час.

Задача 1.3. На испытание поставлено N = 400 изделий. За время t = 3000 час отказало 200 изделий, т.е. n(t) = 400-200=200.За интервал времени (t, t+Δt) , где Δt= 100 час, отказало 100 изделий, т.е. Δn(t)= 100. Требуется определить Р*(3000), P*(3100), f*(3000), λ*(3000).

Задача 1.4. На испытание поставлено 6 однотипных изделий. Получены следующие значения t_i (t_i - время 6езотказной работы i-го изделия) : t₁ =280 час; t₂ = 350 час; t₃ =400 час; t₄ =320 час; t₅ =380 час; t₆ =330 час.

Определить статистическую оценку среднего времени безотказной работы изделия.

Задача 1.6. В результате наблюдения за 45 образцами радиоэлектронного оборудования получены данные до первого отказа всех 45 образцов, сведенные в табл.1.1. Требуется определить m_е*.

Таблица 1.1

Δti, час.	ni	Δti, час.	ni	Δti, час.	ni
0-5		30-35		60-65
5-10		35-40		65-70
10-15		40-45		70-75
15-20		45-50		75-80
20-25		50-55		−	−
25-30		55-60		−	−