Синтез адаптивної системи методом функцій Ляпунова

Метод функцій Ляпунова є одним з основних методів дослідження вустойчивости і якості руху нелінійних систем, що описуються звичайними диференціальними рівняннями. Метод знайшов глибоке і ефективне приложение до проблеми синтезу адаптивних систем управління.

Пояснимо ідею застосування методу функцій Ляпунова на прикладі синтезу алгоритма адаптивного управління для лінійного стаціонарного об'єкту управління .

Постановка завдання. Нехай об'єкт управління(ОУ) описується рівнянням стану:

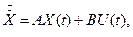
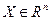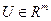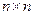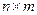де - вектор стану ОУ; - вектор керування; А,В - і постійні матриці параметрів ОУ.

Передбачається доступність виміру усього вектору стану ОУ, так що

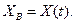
Розглянемо завдання забезпечення ОУ бажаної динаміки, яку задамо з попотужністю еталонної моделі

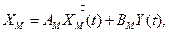
де 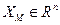-вектор стану еталонної моделі, 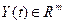- задаюча дія.

Вибір еталонної моделі залежить від вимог, що пред'являються до замкнутої системи(часу перехідного процесу, перерегулювання, астатизму і так далі). При цьому, природно, вона має бути стійкою, тобто матриця Ам - гурвицева.

Вважатимемо, що вектор параметрів 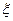ОУ, що складається з коефіцієнтів матриц А, В, заздалегідь не визначений. Відомо лише, що 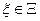. Множина 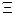можна задати, наприклад, за допомогою максимальних і мінімальних значень, які могут приймати параметри ОУ залежно від умов виготовлення і функционирования.

Формалізуємо мету управління(ЦУ), зажадавши, щоб

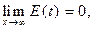
где 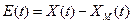- похибка системи.

Таким чином, відповідно до раніше розглянутої класифікації ставиться задача побудови СНС з явною еталонною моделлю. Вирішимо завдання на основі прямого адаптивного підходу. Відповідно до дворівневої структури СНС вирішуватимемо задачу в два етапи: побудова основного контура і синтез контура адаптації.

Синтез основного контура. Завдання вирішується в припущенні, що параметри ОУ відомі. Для отримання структури "ідеального" регулятора запишемо уравнение у відхиленнях

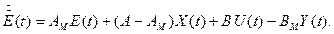
Зажадаємо виконання умови вирішуваної рівняння

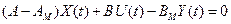
відносно 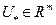при будь-кому 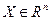, 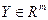. При цьому рівняння матиме вигляд

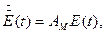
рішення якого асимптотично стійко в силу гурвицевости матриці Ам, і, отже, в ідеальних умовах ЦУ досягається.

Ідеальне управління, що задовольняє співвідношенню(3.25), описується уравнением

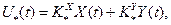котре можно записати у вигляді

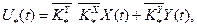(3.26)

где 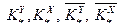- матриці ідеальних коефіцієнтів регулятора, удовлетворяющие рівнянням:

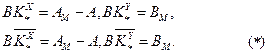
Умови(*) часто називають умовами узгодженості моделі і ОУ, і вони визначають можливість рішення поставленої задачі в умовах точного знання параметрів ОУ. Помітимо, що відповідно до(3.27) матриці ідеальних коеффицієнтів регулятора залежать від конкретних параметрів ОУ 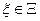. Тому в ситуації невизначеності параметрів ОУ доцільно настроювати матриці коефіцієнтів регулятора для досягнення в системі ЦУ.

Виберемо структуру основного контура відповідно до(3.26) у виді

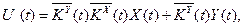(3.28)

де 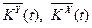- матриці коефіцієнтів регулятора, що настроюються.

Підставляючи отримуємо опис узагальненого настраіваємого об'єкту(ВОНО), що складається з ОУ, моделі і регулятора основного контура, у формі

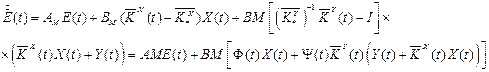
де І - 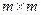единична матрица, 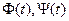- матрици відхилень коеффіцієнтів регулятора від «ідеальних» значень

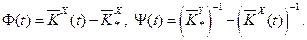
Структура ОНО показана на рис. 3.6.

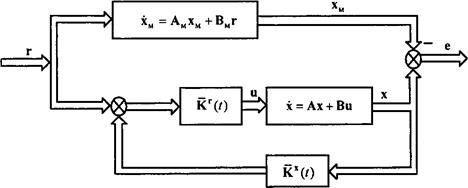
Рис. 3.6. Структурна схема обобщенного настраіваємого объекта

Синтез контура адаптаціі. Для синтеза алгоритмів настройки матриць 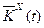і 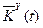запишемо рівняння ОНО у вигляді

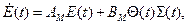
где 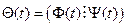- расширенна матрица відхилень настраиваемых коэффи­циентів від їх «ідеальних» значень,

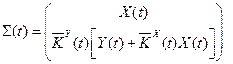
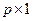- вектор сенсорів(вектор, елементи якого є вимірними або вичислимыми на основі вимірів функціями), .

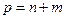Розглянемо в якості претендента на роль функції Ляпунова квадратичну скалярну функцію виду

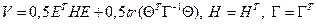
Тут trD означає суму елементів головної діагоналі матриці D(слід матрицы).

Визначимо похідну функції, використовуючи рівняння ОНО

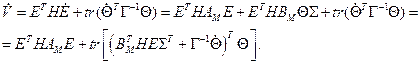
Неважко помітити, що якщо алгоритм адаптації вибрати у виді

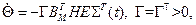
то функція V має властивості

V > 0 и V < 0,

т.е. являєтся функцією Ляпунова.

Останнє твердження виходить з гурвицевости матриці Ам, для якої в силу леми Ляпунова існує Н = Н^T > 0 , що задовольняє матричному рівнянню 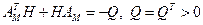, и,следовательно,

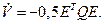(3.34)

Таким чином, система (3.31), (3.33) стійка і в силу (3.34) ЦУ 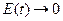при 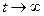досягається. Так как V (3.34) обладне містить в явному виді що настроюються параметрів, то з приведених міркувань слідує лише обмеженість матриці .

Умови ідентифікваності. Посилимо завдання, зажадавши, щоб адаптивна система була асимптотично стійкою, тобто виконувалися властивості

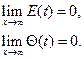
Остання умова еквівалентно вимозі

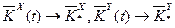при ,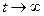

що означає наділ алгоритму ідентифікуючими властивостями.

Припустимо, що компоненти вектору 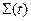- обмежені функції часу.

Тоді із стійкості системи (3.31), (3.33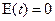) и при 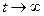следует

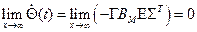
и, следовательно, 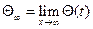- постоянная матрица.

Розглянемо траекторію, вдоль котрих 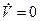или 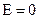. Из (3.31) отримаємо

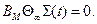(4.36)

Пусть В_м - матрица полного ранга, тогда з (3.36) следует тождество

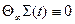(3.37)

Обозначим 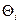- вектор-столбец матрицы 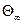и 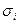- элемент вектора 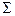. Це по­зволяє записати (3.37) у вигляді

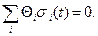(3.38)

Припустимо, що 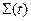- периодический вектор 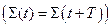, елементи якого є сигналами з частотними компонентами, що розрізняються. Це означає, що 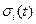- лінійно незалежні функції часу. При цьому рівняння(4.38) має тільки тривіальне рішення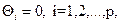

так що

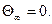
Таким чином, в припущенні періодичності вектору 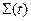з 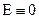следует .

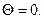Проведений аналіз стійкості дозволяє сформулювати наступну теорему. Теорема 4.1. Пусть 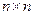матрица А_м является устойчивой, 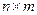матрица В_м -полного ранга, 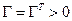- 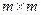матрица, 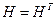- 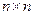матрица, удовлетво­ряющая уравнению Ляпунова

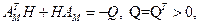(3.39)

И 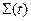- 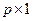вектор ограниченных функций. Тогді система 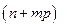дифференці­альних рівнянь (3.31), (3.33)

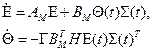
Стійка і 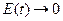при 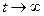. Більше того, якщо р компонент вектору -сигналы зі взаємно різними частотними компонентами, то система(4.31),(4.33) асимптотично стійка в цілому.

Таким чином, теорема 3.1 зводить завдання синтезу адаптивної системи управления до конструювання структури основного контура, що забезпечує приведення опису ВОНО до виду(4.31) і використання для налаштування невідомих параметрів регулятора(чи самого ОУ) алгоритму(3.33). При цьому у вектор сенсорів повинні входити лише вимірювані або обчислювані на основі вимірів ограніченные функції часу, а матриці Ам, Г, Н задовольняти умовам теореми.

Для реалізації алгоритму адаптації слід записати рівняння(3.33) в терминах матриць коефіцієнтів, що настроюються 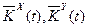. Дня цього досить представити Г у виді

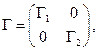
де 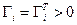- квадратні матриці відповідних розмірів. При цьому система(4.33) записується у виді

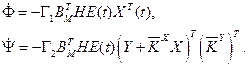
використовуя равенства (4.30), з урахуванням 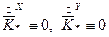отримаємо

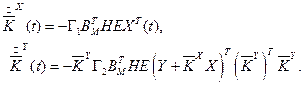
Структурная схема адаптивної системи ((4.31), (4.33)) з урахуванням структури ОНО

(рис. 3.6) приведена на рис. 3.7.

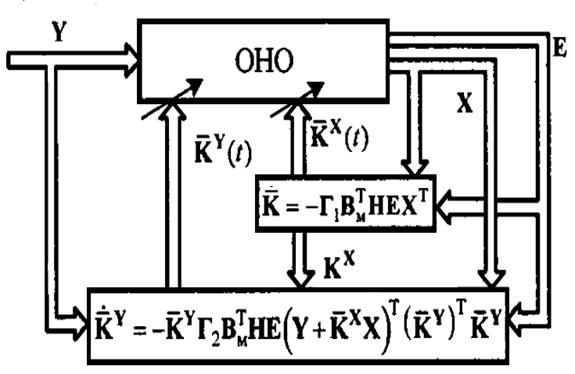
Рис. 3.7. Структурна схема адаптивного керування лінейним ОНО

__________________________________

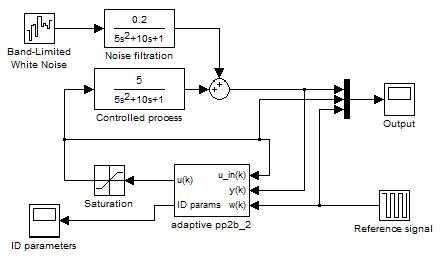
Рис. 3.8. Блок схема адаптації повздожнього руху

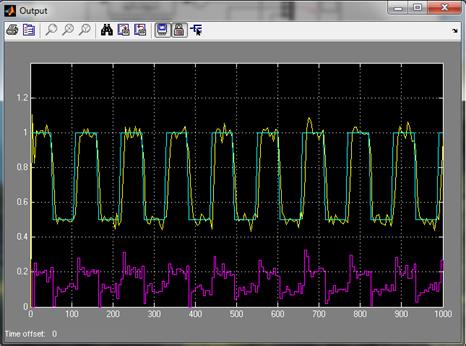
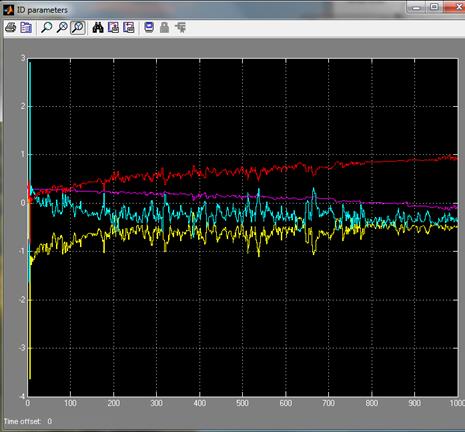
Висновки

У даном курсовому проекті було расмотренно подовжній рух, для якого був побудована адаптація. Було смодуліровано в програмному забезпеченні Mathlab в Simulink блок схема адаптації подовжнього руху і були отримані графіки параметрів і адаптивного управління.