Аддитивная модель сезонных явлений
Несмотря на то, что для экономических временных рядов мультипликативная модель обычно оказывается наиболее подходящей, иногда требуется аддитивная модель. Рассмотрим аддитивную модель сезонных явлений с линейным ростом, предложенную Г. Тейлом и С. Вейджем.
Построение такой модели имеет целью упрощение процедуры прогнозирования, поскольку комбинация мультипликативной сезонной модели с линейным ростом математически громоздка. Кроме того, на практике чаще встречаются экспоненциальные тенденции, чем линейные. Поэтому замена значений первоначального временного ряда их логарифмами преобразует экспоненциальную тенденцию в линейную и одновременно мультипликативную сезонную модель в аддитивную. Тогда временной ряд (исходный или преобразованный) можно представить следующим образом:
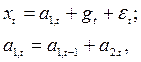
где a1,t— величина уровня процесса после элиминирования сезонных колебаний;
a2,t — аддитивный коэффициент роста;
gt — аддитивный коэффициент сезонности;
εt — белый шум.
Сначала рассмотрим адаптивную процедуру обновления значения 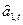 . B момент t мы располагаем наблюдением xt , о котором известно, что
. B момент t мы располагаем наблюдением xt , о котором известно, что
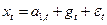
Однако о шуме и сезонном факторе gt никакой информации нет. Величину εt заменим нулем, а в качестве заменителя для gt возьмем самую последнюю оценку сезонного фактора gt-l , где l — период сезонного цикла. Величину 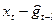 будем рассматривать как новое ≪фактическое≫ значение a1,t. Последней оценкой уровня а1 является
будем рассматривать как новое ≪фактическое≫ значение a1,t. Последней оценкой уровня а1 является 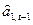 , но она соответствует моменту t-1, а не t.
, но она соответствует моменту t-1, а не t.
Поэтому необходимо к 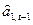 добавить еще
добавить еще 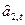 .Но так как оценку
.Но так как оценку 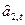 мы еще не можем получить, то вместо нее берем оценку
мы еще не можем получить, то вместо нее берем оценку 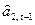 , полученную на предыдущем шаге.
, полученную на предыдущем шаге.
Это приводит к следующей процедуре адаптации:
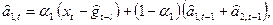
которая при данных весах 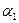 и
и 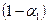 оценивает а1,tчерез наиболее свежее наблюдение xt и ранее подсчитанные величины
оценивает а1,tчерез наиболее свежее наблюдение xt и ранее подсчитанные величины 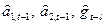 .
.
Та же процедура применяется для получения оценки gt. Новое «фактическое» значение сезонного фактора будет 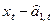 , а старое значение равно
, а старое значение равно 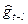 , экспоненциально-сглаженное значение
, экспоненциально-сглаженное значение
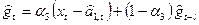
Все три параметра сглаживания будут удовлетворять условию 0< α1, α2, α3 <1.
Адаптивное прогнозирование теперь провести сравнительно просто. Предположим, что t — текущий момент времени, так что 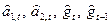 имеются в нашем распоряжении. Предположим также, что мы хотим получить прогноз величины xt+τ(прогноз на τшагов вперед). Экстраполируем тенденцию линейного роста, используя самое последнее значение коэффициента
имеются в нашем распоряжении. Предположим также, что мы хотим получить прогноз величины xt+τ(прогноз на τшагов вперед). Экстраполируем тенденцию линейного роста, используя самое последнее значение коэффициента 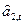 , добавляем самую свежую оценку сезонного члена для этой фазы цикла и пренебрегаем шумом. В результате получаем
, добавляем самую свежую оценку сезонного члена для этой фазы цикла и пренебрегаем шумом. В результате получаем
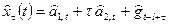
при условии, что 0 < τ< l. Если l < τ< 2l, то необходимо 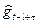 заменить на
заменить на 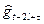 .
.
Однако на практике удобнее осуществлять адаптивное регулирование 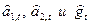 с помощью уравнений, связывающих эти величины с ошибкой прогноза, сделанного в конце периода t — 1 на один шаг вперед.
с помощью уравнений, связывающих эти величины с ошибкой прогноза, сделанного в конце периода t — 1 на один шаг вперед.
