Свойства МНК-оценок. Теорема Гаусса-Маркова

Естественно возникает вопрос: как соотносятся полученные значения b₀ и b₁ с истинными значениями b₀ и b₁ или, другими словами, каково качество МНК-оценок b₀ и b₁. Для ответа на этот вопрос рассмотрим некоторые свойства этих оценок в рамках классической модели.

1. Полученные по МНК оценки b₀ и b₁ являются несмещенными, т.е.

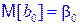и .

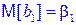% Для доказательства этого утверждения потребуются первое и четвертое условия Гаусса-Маркова. Действительно,

,

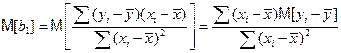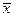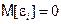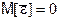поскольку величины x₁, …, x_n и не случайны и содержащие только их выражения можно вынести из-под знака математического ожидания. Далее, поскольку и , то

.

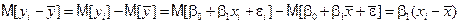Подставляя это выражение в предыдущую формулу, найдем, что .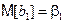

Аналогично находим

. &

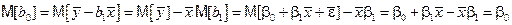2. Полученные по МНК оценки b₀ и b₁ состоятельные.

% Докажем, что МНК-оценки состоятельные, т.е. сходятся по вероятности к истинным значениям:

.

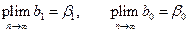Для несмещённых оценок достаточным условием состоятельности является сходимость их дисперсий к нулю при неограниченном возрастании объёма выборки. Это следует из неравенства Чебышёва:

,

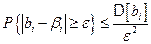поэтому при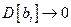

,

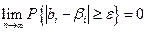т.е. оценки состоятельны. Осталось только показать, что .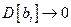

Вычислим дисперсию b₁. Учитывая (5.22), получим

.

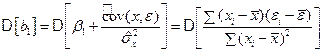Примем во внимание, что 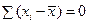, тогда (учитывая второе условие Гаусса-Маркова: 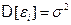), получим

.

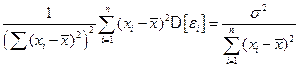В результате, получаем

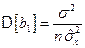. (5.24)

Найдём теперь дисперсию b₀. Принимая во внимание, что 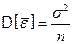, а также (5.23), получим

.

.

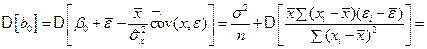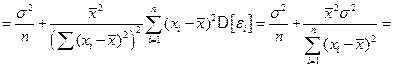
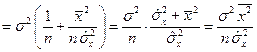В результате, получаем

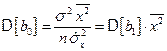. (5.25)

Как можно видеть из (5.24) и (5.25),

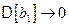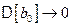и при ,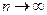

а это будет иметь место в том случае, если x_i не совпадают со своим средним значением (кроме, быть может, конечного числа значений). Итак, МНК-оценки параметров регрессии b₀ и b₁ состоятельны. &

Из соотношений (5.24) и (5.25) можно сделать следующие выводы.

· Дисперсии b₀ и b₁ прямо пропорциональны дисперсии случайного отклонения s². Следовательно, чем больше фактор случайности, тем менее точными будут оценки.

· Чем больше число n наблюдений, тем меньше дисперсии оценок. Это вполне логично, т.к. чем большим числом данных мы располагаем, тем вероятнее получения более точных оценок.

· Чем больше дисперсия (разброс значений 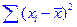) объясняющей переменной, тем меньше дисперсия оценок коэффициентов. Другими словами, чем шире область изменений объясняющей переменной, тем точнее будут оценки (тем меньше доля случайности в их определении).

3. Полученные по МНК оценки b₀ и b₁ коррелированы и

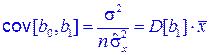. (5.26)

Теперь возникает вопрос, являются ли оценки b₀ и b₁ параметров b₀ и b₁ «наилучшими»? Ответ на этот вопрос дает следующая теорема.

4. Теорема Гаусса-Маркова. Если в регрессионной модели

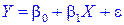, (5.27)

X – детерминированная величина, а случайное отклонение e удовлетворяет условиям 1⁰-3⁰, то оценки b₀ и b₁, полученные по МНК, имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Напомним, что в англоязычной литературе такие оценки называются BLUE-оценками (Best Linear Unbiased Estimator – наилучшие линейные несмещенные оценки).

Доказательство*. Покажем, что МНК-оценки являются «наилучшими» (в смысле наименьшей дисперсии) в классе всех линейных несмещенных оценок.

Представим формулы определения коэффициентов b₀ и b₁ в виде линейных функций относительно значений Y:

,

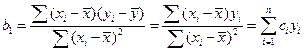где 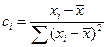. Аналогично получаем:

.

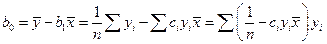Обозначив 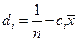, имеем

.

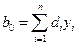Пусть 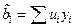– любая другая несмещенная оценка. Представим u_i в виде 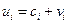, тогда, учитывая (5.20), получим

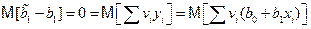
для любых b₀ и b₁. Отсюда следует, что

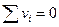и .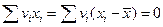

Тогда

.

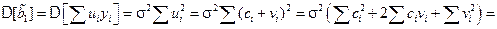
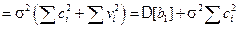Здесь учтено, что 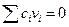в силу определения c_i и того, что 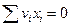. Таким образом, получаем 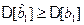, что и требовалось доказать.

Аналогичные вычисления показывают, что . &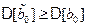

Отметим, что в случае нормальной классической модели МНК дает эффективные оценки, совпадающие с оценками, полученными методом максимального правдоподобия. Таким образом, МНК идеально приспособлен для получения эффективных оценок в случае нормальной классической линейной модели. Другие методы в этих условия в лучшем случае только повторят тот же результат.

Таким образом, в классической линейной регрессионной модели, где случайное отклонение удовлетворяет условиям Гаусса-Маркова и отсутствуют другие сложности, базовым критерием для получения оценок коэффициентов является МНК. Это связано с тем, что оценки, полученные МНК, в соответствии с теоремой Гаусса-Маркова, будут состоятельными, несмещенными и оптимальными как на больших выборках, так и на малых. Однако в реальных ситуациях условия Гаусса-Маркова часто нарушаются. В таких случаях приходится модифицировать МНК, или вообще использовать другие методы.

Дополнение 1.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ В МАТРИЧНОМ ВИДЕ

Парное линейное уравнение регрессии может быть записано в матричном виде:

,

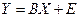где Y – случайный вектор-столбец размерности (n´1) наблюдаемых значений результативного признака; B – вектор-столбец размерности (2´1) подлежащих оценке параметров модели (коэффициентов регрессии); X=(x₀, x₁) – матрица размерности (n´2) наблюдаемых значений факторных признаков. При этом x₀=1 и связано с наличием в уравнении регрессии свободного члена, а x₁ – собственно реальные значения включенного в уравнение регрессии фактора; E – случайный вектор-столбец размерности (n´1) ошибок наблюдений.

.

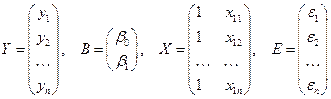В матричной форме применение МНК записывается следующим образом:

.

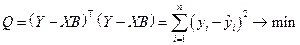Дифференцируя Q по вектору B и приравнивая частные производные по B к нулю, получим:

.

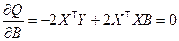Учитывая обратимость матрицы 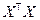, находим МНК-оценку вектора B:

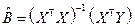, (5.28)

где .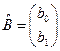

Пример 5.2. Получить оценки коэффициентов регрессии матричным способом, используя данные примера 5.1.

Решение. В случае примера 5.1 исходные матрицы имеют вид

, .

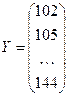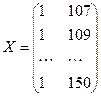Тогда

.

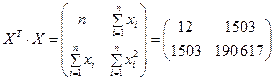Находим обратную матрицу

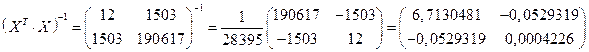
и

.

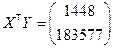В результате вектор оценок коэффициентов регрессии будет равен

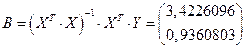. Ÿ

Дополнение 2.
ОЦЕНКА ПАРАМЕТРОВ РЕГРЕССИИ
МЕТОДОМ МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ

Наряду с методом наименьших квадратов (МНК) возможен и другой подход к оцениванию параметров линейного регрессионного уравнения по данным наблюдений – метод максимального правдоподобия (ММП) (см. дополнение 2 к лекции 2). ММП обычно не предъявляет требований к свойствам малых выборок, а в случае корректной спецификации модели и при выполнении некоторых условий обеспечивает асимптотическую несмещенность, состоятельность и асимптотическую эффективность. Более того, они предоставляют возможность для проведения тестов, которые не могли использоваться в случае МНК.

Отметим, что для нормальной классической линейной регрессионной модели ММП, по сравнению с МНК, не даёт никаких преимуществ. Если случайные отклонения модели распределены по другому закону, то, вообще говоря, выражения для оценки коэффициентов регрессии, полученные на основе ММП, будут отличаться от их аналогов, полученных с использованием МНК. Конечно МНК обладает большими достоинствами по сравнению с ММП, если выполняются условия Гаусса-Маркова, однако все они быстро теряются, если эти условия нарушаются.

Для применения ММП должен быть известен вид закона распределения вероятностей имеющихся выборочных данных.

В рамках нормальной классической регрессионной модели значения y_i можно рассматривать как независимые нормально распределённые случайные величины с математическим ожиданием 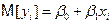, являющимся функцией от x_i, и постоянной дисперсией s². Следовательно, плотность нормально распределенной случайной величины y_i имеет вид

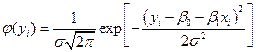. (5.29)

Функция правдоподобия, выражающая плотность вероятности совместного появления результатов выборки, имеет вид

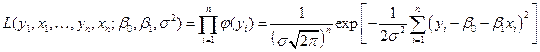. (5.30)

Согласно ММП в качестве оценок параметров b₀, b₁ и s² принимаются такие значения 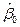, 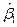и 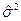, которые максимизируют функцию правдоподобия L. Так как функции L и lnL одновременно достигают своего максимума, достигают искать максимум логарифма функции правдоподобия:

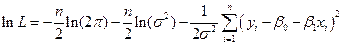. (5.31)

Необходимые условия экстремума функции lnL имеют вид:

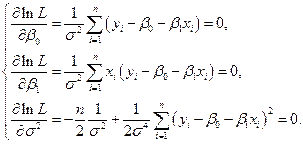(5.32)

Решением системы уравнений (5.32) являются оценки

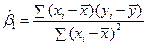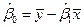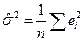, , . (5.33)

Отметим, что ММП-оценки параметров b₁ и b₀ совпадают с соответствующими МНК-оценками. Это легко видеть из того, что первое и второе уравнения (5.32) совпадают с соответствующими уравнениями МНК. Заметим, что ММП-оценка для s² является смещенной и не совпадает с соответствующей МНК-оценкой.

ЛЕКЦИЯ 4 81

Глава 5. ПАРНАЯ ЛИНЕЙНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ 81

§5.1. Модель парной линейной регрессии 81

5.1.1. Проблема оценивания связи экономических переменных 81

5.1.2. Основные задачи регрессионного анализа 82

5.1.3. Модель простой линейной регрессии 85

5.1.4. Метод наименьших квадратов 86

5.1.5. Условия Гаусса-Маркова. Классическая линейная регрессионная модель 91

5.1.6. Свойства МНК-оценок. Теорема Гаусса-Маркова 94

Дополнение 1. Метод наименьших квадратов в матричном виде 96

Дополнение 2. Оценка параметров регрессии методом максимального правдоподобия 97

[1] В англоязычной литературе он называется ordinary least square (OLS) method.