Чему равны моменты сопротивления при изгибе для балок прямоугольного и круглого поперечных сечений?
Для прямоугольного поперечного сечения (см. рис. 4.4) момент сопротивления при изгибе относительно нейтральной оси x равен:
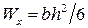 .
.
Из этой формулы видно, что при той же самой площади поперечного сечения балки ее момент сопротивления существенно возрастает с увеличением высоты балки h.
Если балка имеет квадратное поперечное сечение со стороной a, то
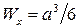 .
.
В случае круглого поперечного сечения балки момент сопротивления при изгибе равен
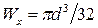 .
.
Заметим, что для катанных профилей, таких, например, как швеллер, двутавр и уголок, значения моментов сопротивления балки при изгибе (а также другие геометрические характеристики) определяются по сортаментам, которые приводятся в приложениях практически к каждому учебнику по сопротивлению материалов.
7.26. Чему равны нормальные напряжения при поперечном изгибе балки?
В отличие от чистого изгиба, при поперечном изгибе в сечении балки помимо изгибающего момента 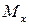 возникает и перерезывающая сила
возникает и перерезывающая сила  . Поэтому в поперечном сечении наряду с нормальными напряжениями
. Поэтому в поперечном сечении наряду с нормальными напряжениями 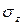 возникают и касательные напряжения
возникают и касательные напряжения 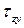 .
.
На основании закона парности касательных напряжений в продольных сечениях балки возникают касательные напряжения 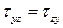 .
.
Возникновение касательных напряжений 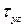 в плоскостях, параллельных нейтральной плоскости, покажем на следующем простом примере.
в плоскостях, параллельных нейтральной плоскости, покажем на следующем простом примере.
Мысленно представим себе балку прямоугольного поперечного сечения высотой h, шарнирно опертую по концам. Поместим поверх этой балки точно такую же балку. Приложим к этим двум балкам посредине пролета сосредоточенную силу P. Если пренебречь трением между этими балками, изгиб каждой из них будет происходить независимо от изгиба другой балки. При этом у обеих балок будут сжаты верхние и растянуты нижние волокна. В результате нижние продольные волокна верхней балки сместятся относительно верхних волокон нижней балки.
Иную картину мы будем наблюдать в сплошной балке высотой 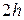 . Никакого смещения верхней части балки относительной нижней мы, естественно, не обнаружим. Отсутствие этого смещения и объясняется возникновением, в данном случае в нейтральном слое, касательных напряжений
. Никакого смещения верхней части балки относительной нижней мы, естественно, не обнаружим. Отсутствие этого смещения и объясняется возникновением, в данном случае в нейтральном слое, касательных напряжений 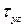 .
.
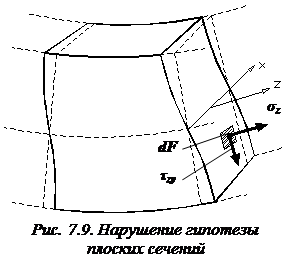
Поскольку при поперечном изгибе в поперечных сечениях стержня возникают касательные напряжения 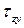 , поперечные сечения балки искривляются (рис. 7.9) и, следовательно, гипотеза плоских сечений нарушается.
, поперечные сечения балки искривляются (рис. 7.9) и, следовательно, гипотеза плоских сечений нарушается.
 Однако теоретические и экспериментальные исследования показали, что если балка является достаточно длинной (
Однако теоретические и экспериментальные исследования показали, что если балка является достаточно длинной ( 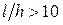 ), то влияние искривления поперечного сечения на значения нормальных напряжений невелико.
), то влияние искривления поперечного сечения на значения нормальных напряжений невелико.
Поэтому влиянием сдвигов на закон распределения нормальных напряжений при изгибе пренебрегают и нормальные напряжения вычисляют по той же самой формуле(7.6).
7.27. По какой формуле вычисляются касательные напряжения при поперечном изгибе?
Вырежем из балки прямоугольного поперечного сечения (рис. 7.10, а) элемент длиной 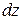 и дополнительным продольным сечением рассечем его на две части (рис. 7.10, б).
и дополнительным продольным сечением рассечем его на две части (рис. 7.10, б).




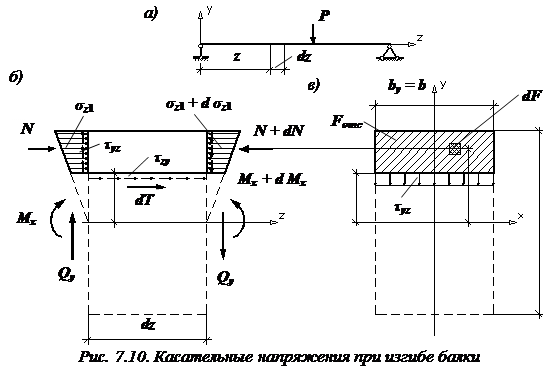
Рассмотрим равновесие верхней части, в поперечных сечениях которой из-за отличия изгибающих моментов возникают разные сжимающие напряжения. Для того чтобы эта часть балки находилась в равновесии (то есть выполнялось условие равновесия 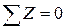 ), в ее продольном сечении должна возникнуть касательная сила
), в ее продольном сечении должна возникнуть касательная сила 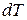 . Тогда
. Тогда
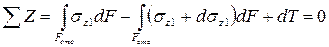 .
.
Отсюда
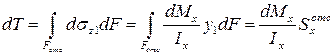 , (7.7)
, (7.7)
где интегрирование ведется только по отсеченной части площади поперечного сечения балки 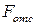 .
.
Эта часть площади (рис. 7.10, в) нами заштрихована.
В формуле (7.7) 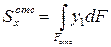 – статический момент отсеченной (заштрихованной) части площади поперечного сечения относительно нейтральной оси x.
– статический момент отсеченной (заштрихованной) части площади поперечного сечения относительно нейтральной оси x.
Будем предполагать, что касательные напряжения 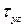 , возникающие в продольном сечении балки, равномерно распределены по ее ширине
, возникающие в продольном сечении балки, равномерно распределены по ее ширине 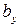 в месте сечения. Это допущение, известное под названием гипотезы Журавского, справедливо только в том случае, когда ширина поперечного сечения много меньше его высоты, то есть сечение является узким.
в месте сечения. Это допущение, известное под названием гипотезы Журавского, справедливо только в том случае, когда ширина поперечного сечения много меньше его высоты, то есть сечение является узким.
Тогда 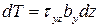 и соответственно
и соответственно 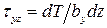 .
.
Учитывая формулу (7.7), найдем, что
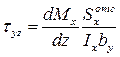 .
.
Но, согласно формуле Шведлера – Журавского, 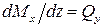 , а
, а 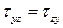 . Тогда окончательно касательные напряжения
. Тогда окончательно касательные напряжения 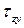 , возникающие в точках поперечного сечении балки, находящихся на расстоянии y от нейтральной оси x,определяются по следующей формуле
, возникающие в точках поперечного сечении балки, находящихся на расстоянии y от нейтральной оси x,определяются по следующей формуле
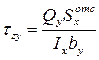 . (7.8)
. (7.8)
Приближенная формула (7.8) впервые была получена в 1855 г. Дмитрием Ивановичем Журавским,и поэтому она носит его имя.
