Задания для самостоятельного решения. 7.1 При каких значениях коэффициента k система (рисунок 7.3) устойчива
7.1 При каких значениях коэффициента k система (рисунок 7.3) устойчива, если W1 = 1/(1+0,1s), W2 = 2/(1 + 0,01s), W3 = k/(1 + s), W4 = 10?
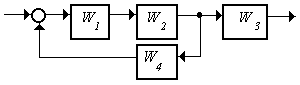
Рисунок 7.3
7.2 Оценить устойчивость системы 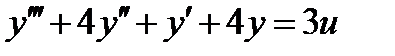 .
.
7.3 С помощью критерия Гурвица, Льенара-Шипара проверить устойчивость системы (рисунок 7.4), если W1 = 5/(1 + 10s), W2 = –1/s, W3 = 100.
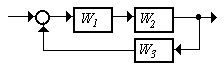
Рисунок 7.4
7.4 Система задана нулями 0±3j и полюсами -1±5j; -1; -10. Оценить устойчивость системы до и после замыкания единичной ООС.
7.5 Устойчива ли система 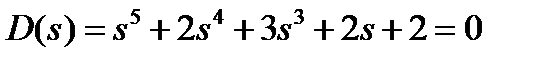 ?
?
7.6 Оценить устойчивость системы по критерию Рауса, Льенара-Шипара
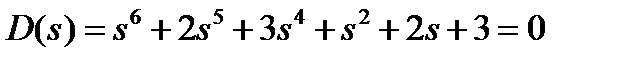 .
.
7.7 Оценить устойчивость системы (рисунок 7.5) по критерию Гурвица
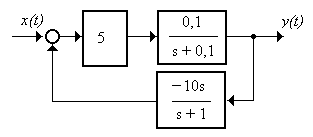
Рисунок 7.5
7.8 Оценить устойчивость системы по критерию Гурвица при 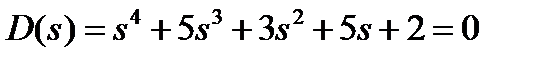 .
.
7.9 Оценить устойчивость системы (рисунок 7.6), если
W1(s) = 1, W2(s) = 2, W3(s) = 3, W4(s) = 1, W5(s) = 6, W6(s) = 10, W7(s) = 2, W8(s) = 2s, W9(s) = 10/(1 + 10s), W10(s) = 1/3, W11(s) = 1/10s.
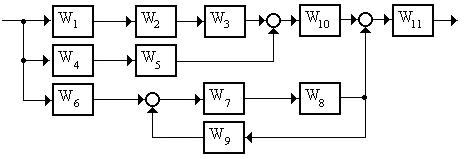
Рисунок 7.6
7.10 Оценить устойчивость по критерию Рауса системы с характеристическим уравнением 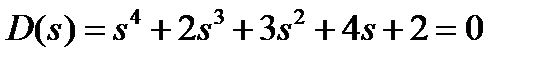 .
.
7.11 Определить устойчивость системы, используя алгебраические критерии устойчивости. Определить критический коэффициент усиления.
Структурные схемы системы и параметры для различных вариантов приведены на рис. 7.7 – 7.11
Схема № 1.
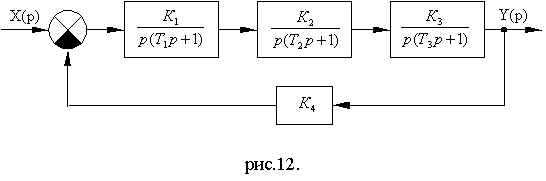
Рис. 7.7
Вариант № 0 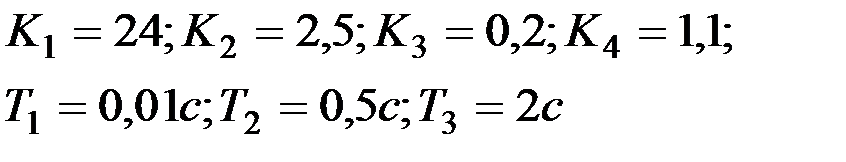 | Вариант № 1 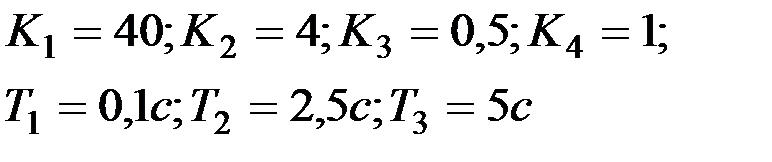 |
Вариант № 10 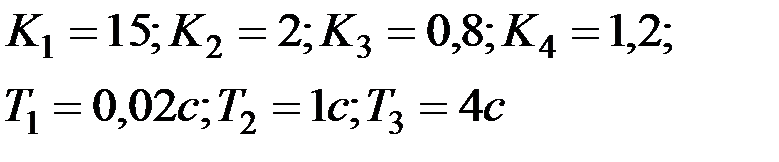 | Вариант № 11 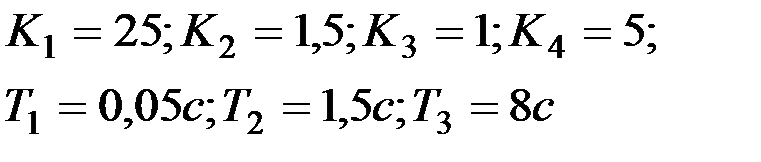 |
Вариант № 12 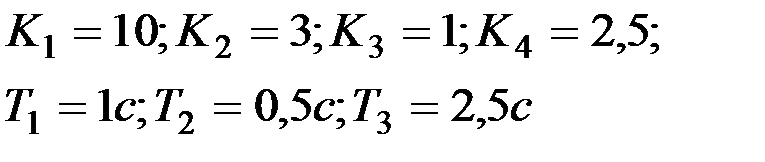 | Вариант № 13 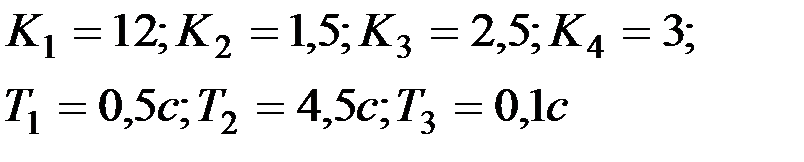 |
Вариант № 14 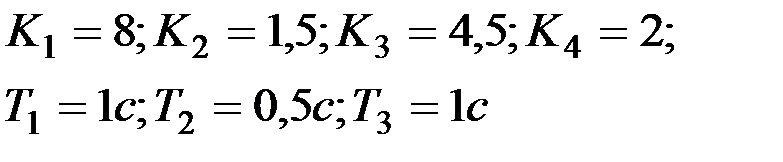 | Вариант № 15 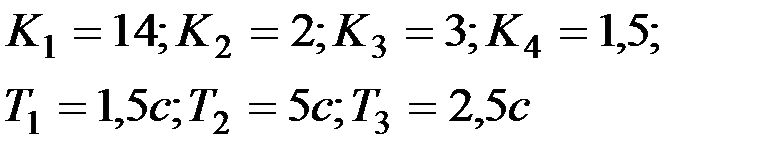 |
Схема № 2.
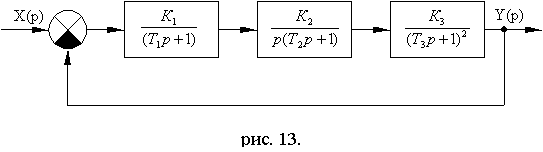
Рис. 7.8
Вариант № 2 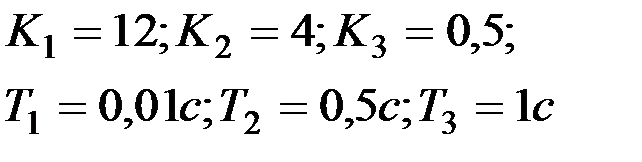 | Вариант № 3 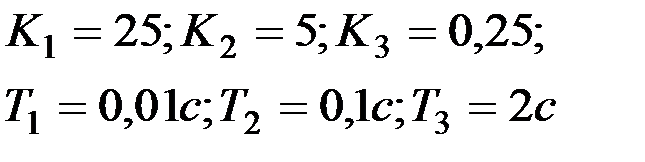 |
Вариант № 16 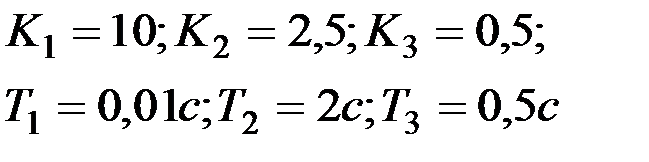 | Вариант № 17 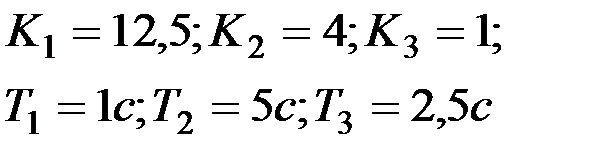 |
Вариант № 18 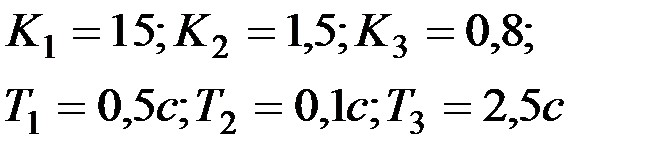 | Вариант № 19 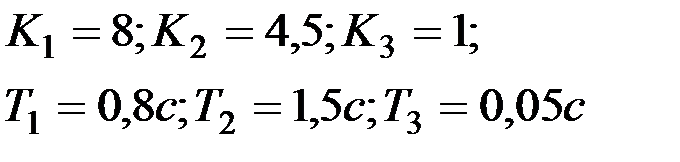 |
Вариант № 20 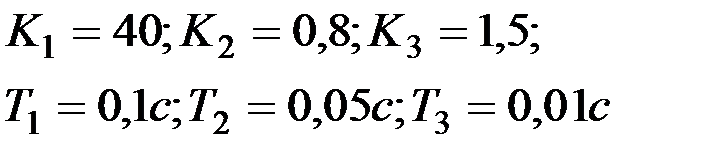 | Вариант № 21 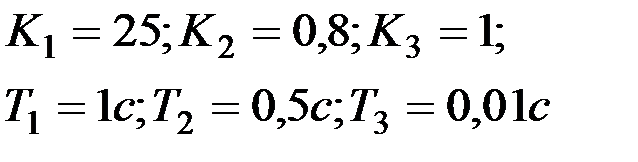 |
Схема № 3
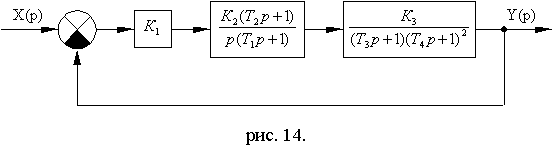
Рис. 7.9
Вариант № 4 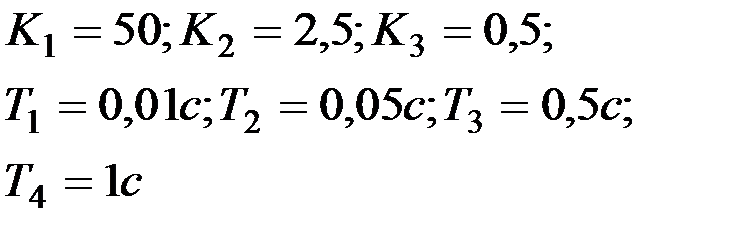 | Вариант № 5 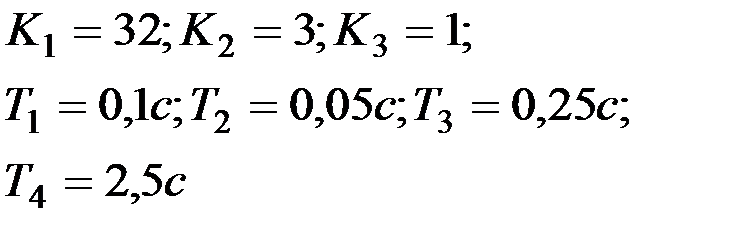 |
Вариант № 22 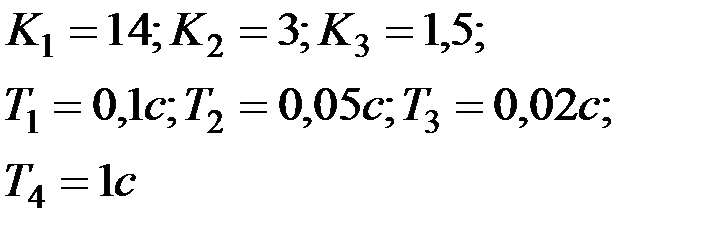 | Вариант № 23 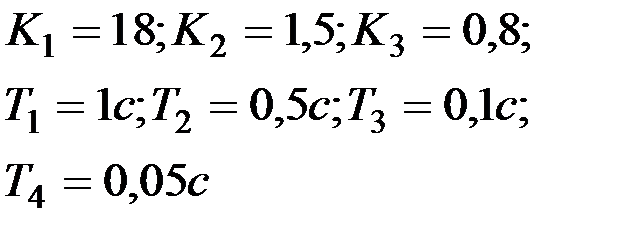 |
Вариант № 24 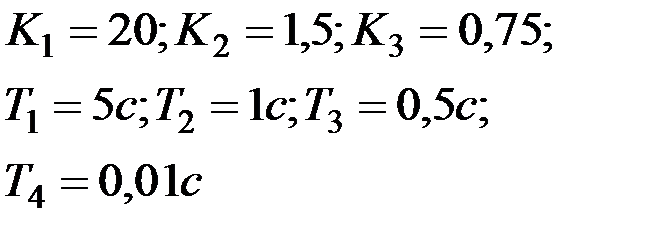 | Вариант № 25 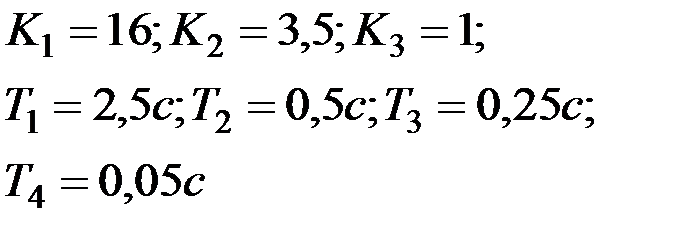 |
Схема№ 4
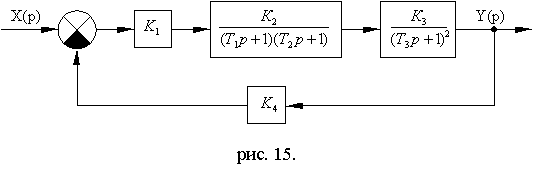
Рис. 7.10
Вариант № 6 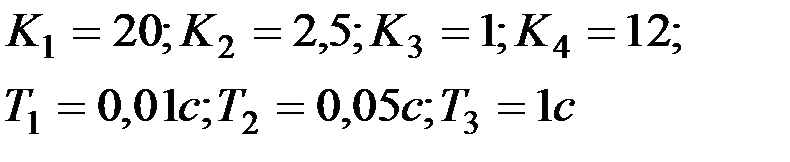 | Вариант № 7 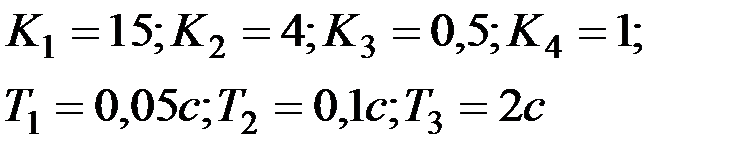 |
Вариант № 26 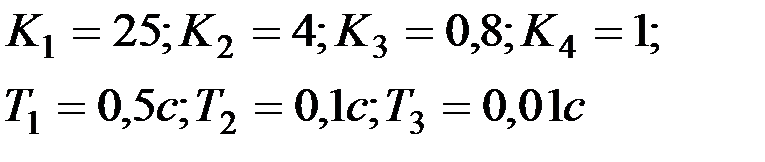 | Вариант № 27 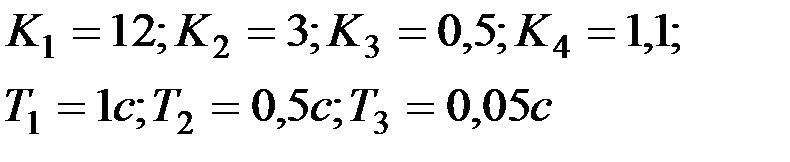 |
Схема № 5
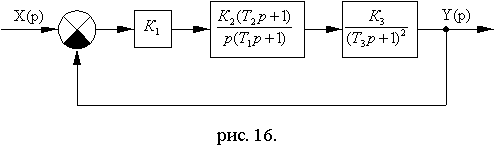
Рис. 7.11
Вариант № 8 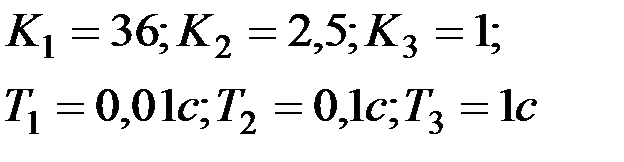 | Вариант № 9 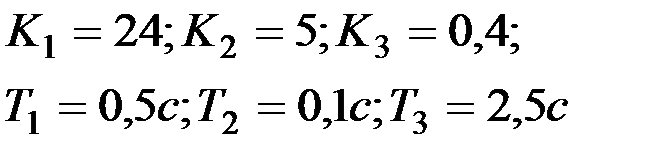 |
Вариант № 28 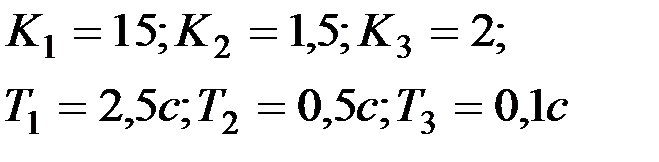 | Вариант № 29 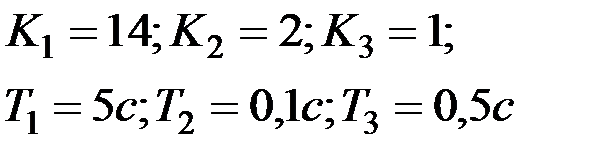 |
Контрольные вопросы:
1. Что понимают под устойчивостью САУ в малом и в большом?
2. Какой вид имеет решение уравнения динамики САУ?
3. Как найти вынужденную составляющую решения уравнения динамики САУ?
4. Какой вид имеет свободная составляющая решения уравнения динамики САУ?
5. Что такое характеристическое уравнение?
6. Какой вид имеют корни характеристического уравнения?
7. Чем отличаются правые и левые корни характеристического уравнения?
8. Сформулируйте условие устойчивости систем по Ляпунову.
9. Что такое граница устойчивости?
10. Что такое критерии устойчивости?
11. Сформулируйте необходимое условие устойчивости САУ.
12. Сформулируйте критерий Рауса.
13. Сформулируйте критерий Гурвица.
14. В чем достоинства и недостатки алгебраических критериев устойчивости?
Практическая работа № 8
Исследование устойчивости линейных систем на основе построения
годографа Михайлова.
Цель работы: Изучение частотного метода исследования устойчивости линейной системы автоматического управления на основе построения
годографа Михайлова.
Задание: Для оценки устойчивости системы по критерию устойчивости Михайлова необходимо выполнить следующие этапы:
- определить передаточную функцию замкнутой системы;
- привести её к дробно-рациональному виду и получить характеристическое уравнение системы;
- в последнем произвести формальную замену оператора р на 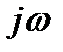 и выделить вещественную
и выделить вещественную 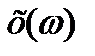 и мнимую
и мнимую 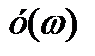 части этого выражения;
части этого выражения;
- задаваясь произвольно значениями 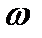 от 0 до
от 0 до 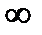 рассчитать значения
рассчитать значения 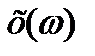 и
и 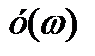 полученные значения свести в таблицу. Рекомендуется посчитать по 2-3 точки для каждого квадранта;
полученные значения свести в таблицу. Рекомендуется посчитать по 2-3 точки для каждого квадранта;
- построить характеристическую кривую Михайлова(годограф) в плоскости 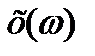 -
- 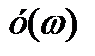 и дать оценку устойчивости системы.
и дать оценку устойчивости системы.
Общие сведения
1. Устойчивость САУ по виду частотных характеристик определяется с помощью частотных критериев, основанных на использовании принципа аргумента Коши, известного из теории функций комплексного переменного. Это критерии Михайлова, Найквиста и D-разбиения.
Критерий устойчивости Михайлова основан на рассмотрении характеристического многочлена 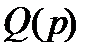 , но имеющего несколько иное представление. Подставим в этот многочлен
, но имеющего несколько иное представление. Подставим в этот многочлен 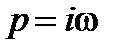 . В результате получим комплексную функцию
. В результате получим комплексную функцию 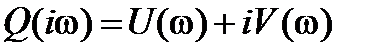 . Вещественная часть
. Вещественная часть 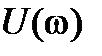 получена из членов многочлена
получена из членов многочлена 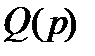 , содержащих четные степени
, содержащих четные степени 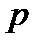 , а мнимая часть
, а мнимая часть 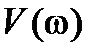 получена из членов
получена из членов 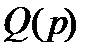 с нечетными степенями
с нечетными степенями 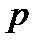 . Функция
. Функция 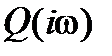 отображается в виде годографа на комплексной плоскости (рисунок 8.1). Этот годограф называют годографом Михайлова. Каждому значению
отображается в виде годографа на комплексной плоскости (рисунок 8.1). Этот годограф называют годографом Михайлова. Каждому значению 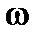 соответствуют определенные значения
соответствуют определенные значения 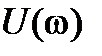 и
и 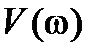 и определенная точка на комплексной плоскости. При
и определенная точка на комплексной плоскости. При 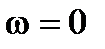 функция
функция 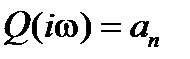 , т.е. годограф начинается на действительной оси. При
, т.е. годограф начинается на действительной оси. При 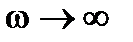
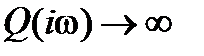 .
.
| V(w) |
| U(w) |
| w®¥ |
| an |
Рисунок 8.1 Годограф Михайлова
Критерий Михайлова формулируется следующим образом: система устойчива, если годограф 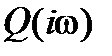 , начинаясь на действительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно
, начинаясь на действительной полуоси, огибает против часовой стрелки начало координат, проходя последовательно 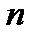 квадратов, где
квадратов, где 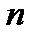 -порядок системы (степень характеристического полинома).
-порядок системы (степень характеристического полинома).
На рисунке 8.1 годограф 1 относится к устойчивой САУ, годографы 3, 4. 5, 6, 7 - к неустойчивой САУ. Если годограф проходит через начало координат (кривая 2 на рисунке 8.1), то система находится на границе устойчивости. Действительно, в этом случае существует значение 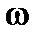 , при котором
, при котором 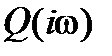 , т.е. характеристическое уравнение системы, имеет пару сопряженных мнимых корней
, т.е. характеристическое уравнение системы, имеет пару сопряженных мнимых корней 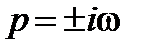 . А это и означает наличие в системе незатухающих колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение параметров системы, в результате которого годограф
. А это и означает наличие в системе незатухающих колебаний, т.е. нахождение ее на границе устойчивости. Незначительное изменение параметров системы, в результате которого годограф 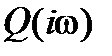 на рисунке 8.1 отойдет влево от начала координат, делает систему устойчивой, а изменение параметров в другую сторону - неустойчивой.
на рисунке 8.1 отойдет влево от начала координат, делает систему устойчивой, а изменение параметров в другую сторону - неустойчивой.
Докажем критерий Михайлова. Представим характеристический многочлен в следующем виде: 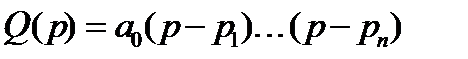 . Рассмотрим комплексную плоскость
. Рассмотрим комплексную плоскость 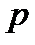 (рисунок 8.2), на которой точками отмечены корни
(рисунок 8.2), на которой точками отмечены корни 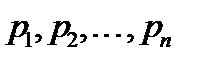 .
.
| Im |
| Re |
| D |
| (k) |
| (n-k) |
| pi |
| pi |
| A |
| iw - pi |
| iw - pi |
Рисунок 8.2 Расположение корней на комплексной плоскости 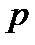
Предположим, что первые 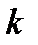 из этих корней лежат справа от мнимой оси, а остальные (
из этих корней лежат справа от мнимой оси, а остальные ( 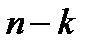 ) корней - слева от мнимой оси. Пусть теперь независимая переменная
) корней - слева от мнимой оси. Пусть теперь независимая переменная 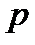 меняется вдоль мнимой оси от минус
меняется вдоль мнимой оси от минус 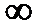 до
до 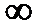 , т.е.
, т.е. 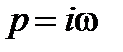 , где
, где 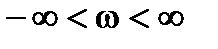 . Пусть точка
. Пусть точка 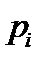 лежит справа от мнимой оси.Построим разность
лежит справа от мнимой оси.Построим разность 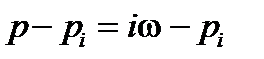 , которая изображена на рисунке 8.2 вектором
, которая изображена на рисунке 8.2 вектором 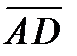 . При изменении
. При изменении 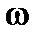 от минус
от минус 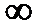 до
до 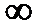 вектор
вектор 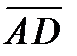 повернется вокруг точки
повернется вокруг точки 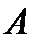 на угол минус
на угол минус 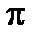 (направленное вращение по часовой стрелке будем считать отрицательным). Таким образом, если корень
(направленное вращение по часовой стрелке будем считать отрицательным). Таким образом, если корень 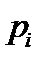 лежит справа от мнимой оси, то приращение аргумента числа
лежит справа от мнимой оси, то приращение аргумента числа 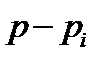 при изменении
при изменении 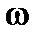 отминус
отминус 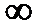 до
до 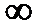 равно минус
равно минус 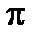 . Если корень
. Если корень 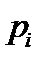 лежит слева от мнимой оси, то приращение аргумента числа
лежит слева от мнимой оси, то приращение аргумента числа 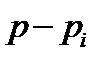 при изменении
при изменении 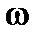 от минус
от минус 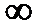 до
до 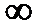 равно
равно 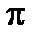 . Приращение аргумента функции
. Приращение аргумента функции 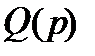 равно
равно
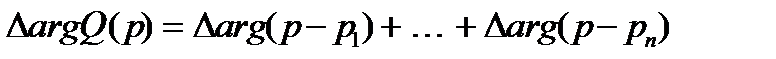 .
.
Отсюда при изменении 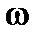 от минус
от минус 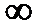 до
до 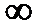 получим
получим
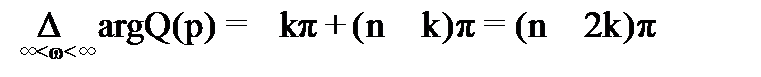
Необходимое и достаточное условие устойчивости состоит в том, что 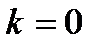 , поэтому для устойчивости системы необходимо и достаточно, чтобы
, поэтому для устойчивости системы необходимо и достаточно, чтобы 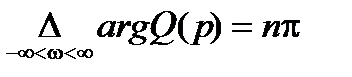 .
. 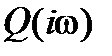 сопряжено с минус
сопряжено с минус 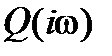 , т.е.
, т.е. 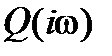 = -
= - 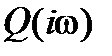 , поэтому годограф
, поэтому годограф 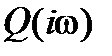 симметричен годографу
симметричен годографу 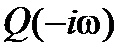 относительно действительной оси
относительно действительной оси 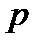 -плоскости, отсюда
-плоскости, отсюда 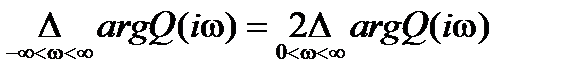 и, следовательно, для устойчивости САУ необходимо и достаточно выполнение условия
и, следовательно, для устойчивости САУ необходимо и достаточно выполнение условия 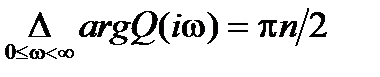 .
.
Примеры годографов Михайлова для устойчивых САУ разных порядков (от 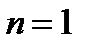 до
до 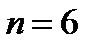 ) изображены на рисунке 8.3.
) изображены на рисунке 8.3.
| n = 1 |
| n=2 |
| n=3 |
| n = 4 |
| n = 5 |
| n = 6 |
| an |
| V(w) |
| U(w) |
Рисунок 8.3 Годографы Михайлова для устойчивых САУ
В данной работе необходимо:
1. Оценить устойчивости линейной системы автоматического управления по критерию Михайлова и выполнить расчеты задания № 1
Задание №1
1. Определить устойчивость автоматической системы с помощью критерия Михайлова, если характеристическое уравнение имеет вид
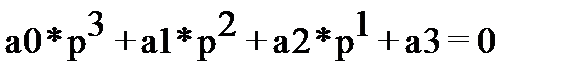
| вариант | а0 | а1 | а2 | а3 |
| 0,004 | 0,5 | |||
| 0,005 | 0,4 | |||
| 0,012 | 0,20 | |||
| 0,058 | 0,8 | |||
| 0,890 | 0,40 | |||
| 0,47 | 0,7 | |||
| 0,65 | 0,1 |
2. Исследовать влияние коэффициента α на устойчивость автоматической системы с помощью критерия Михайлова, если характеристическое уравнение имеет вид
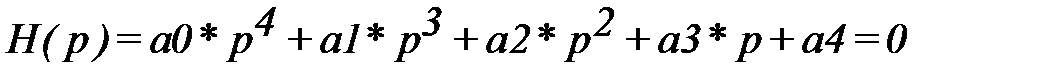
где а0=0,000524 , а1 =0,0589, а2 = 1,014 , а3 = 2,619+35*α , а4=87 ,если коэффициент α принимает значения 0,02; 0,115 ; 0,25 ; 0,4.
3. С помощью критерия Михайлова определить граничное значение коэффициента передачи регулятора Кр, если характеристическое уравнение системы имеет вид
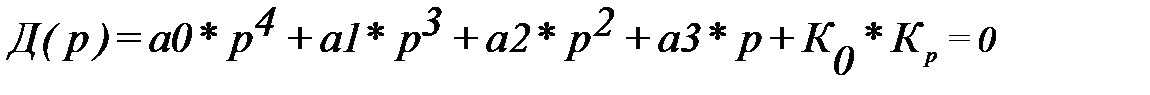
где а0=0,004 , а1 =0,35, а2 = 4,2 , а3 = 30 , Ко=2
4. Определить по критерию Михайлова устойчивость автоматической системы, уравнение свободного движения которой имеет вид
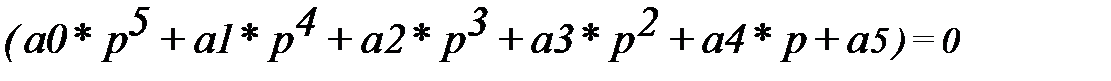
где а0=6*10-4 , а1 =10-2, а2 = 0,2 , а3 = 1, а4 = 1,8, а5 = 2
а0=7*10-4 , а1 =10-2, а2 = 0,8, а3 = 47, а4 = 0,41, а5 = 0
а0=1*10-4 , а1 =10-1, а2 = 0,3 , а3 = 5, а4 = 1,22, а5 = 5
а0=3*10-4 , а1 =10-2, а2 = 0,12 , а3 = 0,8, а4 = 4, а5 = 100
5. Определить устойчивость автоматической системы с помощью критерия Михайлова, для системы со следующей структурной схемой
| Вариант | к1 | к2 | к3 | к4 | Т1 | Т2 | Т3 | Т4 |
| 0,58 | 0,1 | 0,5 | 4,7 | |||||
| 0,34 | 1,5 | 0,1 | 0,6 | 1,5 | ||||
| 0,69 | 7,6 | 0,1 | 0,7 | 6,4 | ||||
| 0,33 | 8,6 | 0,1 | 0,5 | 3,8 | ||||
| 0,10 | 4,5 | 0,1 | 1,0 |
6. Определить устойчивость замкнутой и разомкнутой системы автоматического управления с помощью критерия Михайлова со следующей структурной схемой
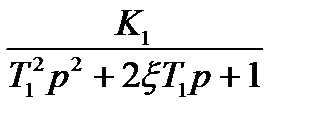 |
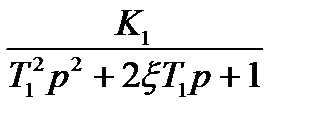 |
К1= 120 Т1= 0,25 ξ=0,05
7. Определить устойчивость замкнутой и разомкнутой системы автоматического управления с помощью критерия Михайлова со следующей структурной схемой
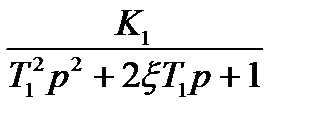 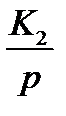 |
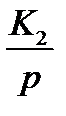 |
К1= 48 Т1= 0,47 ξ=0,5 К2=10
8. Определить устойчивость замкнутой и разомкнутой системы автоматического управления с помощью критерия Михайлова со следующей структурной схемой
