V1: механические волны

I:

S: В выражении для смещения материальной точки 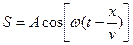в случае гармонических колебаний, символ S означает:

-: амплитуду колебаний

-: фазу волны

-: расстояние между соседними гребнями волн

-: произвольную координату

+: смещение точки, участвующей в волновом процессе

I:

S: В уравнении волны 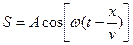символ x представляет собой:

-: смещение точки, участвующей в волновом процессе

+: произвольную координату

-: амплитуду колебаний

-: фазу волны

-: расстояние между соседними гребнями волн

I:

S: Длиной волны называется:

-: расстояние между двумя соседними точками на оси OY, колеблющимися в одинаковых фазах

+: расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах

-: расстояние между двумя соседними точками на оси OX, колеблющимися в противоположных фазах

-: расстояние, пробегаемое волной за единицу времени

-: наибольшее отклонение точек волны от положения равновесия

I:

S: Вектором Умова называют:

+: величину, равную потоку энергии волн, проходящему через единичную площадь, перпендикулярную этому направлению

-: вектор, перпендикулярный направлению распространения волны

-: величину, равную плотности энергии волны

-: величину кинетической энергии, переносимой волной

-: величину, показывающую скорость затухания волны

I:

S: Вектор Умова определяется выражением:

-:

+:

-:

-:

-:

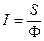
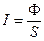
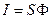
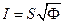
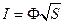
I:

S: В выражении для интенсивности волны 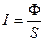величина Ф представляет собой:

-: длину волны

-: амплитуду волны

+: поток энергии волн

-: плотность энергии волн

-: энергию волн

I:

S: Механической волной называется:

-: механические колебания, описываемые по гармоническому закону

-: механическое возмущение, возникающее в твердом теле при его деформации

-: перенос энергии в упругой среде

+: механическое возмущение, распространяющееся в пространстве и несущее энергию

-: периодическое отклонение тела от положения равновесия

I:

S: Уравнение волны записывается в следующем виде:

+:

-:

-:

-:

-:

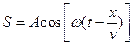
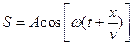
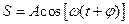
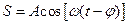
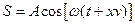
I:

S: Скорость распространения волны определяется выражением:

-:

-:

+:

-:

-:

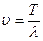
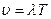
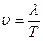
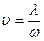
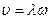
I:

S: За время 4/3 секунды волна распространилась на расстояния равное длине волны. Частота колебаний волны равна:

+: 0,75 Гц

-: 1 Гц

-: 10 Гц

-: 0,25 Гц

-: 250 Гц

I:

S: Скорость распространения звука в материале, в котором колебания с периодом 0,01 с вызывают звуковую волну, имеющую длину 10 м, составляет:

-: 100 м/с

+: 1000 м/с

-: 10 км/с

-: 10 м/с

-: 100 км/с

I:

S: Частота колебаний волны с длиной волны 3 м и скоростью распространения 12 м/с составляет:

-: 0,25 Гц

-: 25 Гц

-: 0,4 Гц

+: 4 Гц

-: 0,5 Гц

V1: СТАТОБРАБОТКА

I:

S: В соответствии с приведенной таблицей коэффициент Стьюдента для пяти измерений и доверительной вероятности 0,98 составляет

n	p
0,7	0,8	0,9	0,95	0,98	0,99
	2,0	3,1	6,3	12,7	31,8	63,7
	1,3	1,9	2,9	4,3	7,0	9,9
	1,3	1,6	2,4	3,2	4,5	5,8
	1,2	1,5	2,1	2,8	3,7	4,6
	1,2	1,5	2,0	2,6	3,4	4,0
	1,1	1,4	1,9	2,4	3,1	3,7

-: 1,2;

-: 2,8;

+: 3,7;

-: 1,9;

-: 2,3.

I:

S: Для шести измерений коэффициенту Стьюдента равному 2,6 соответствует доверительная вероятность

n	p
0,7	0,8	0,9	0,95	0,98	0,99
	2,0	3,1	6,3	12,7	31,8	63,7
	1,3	1,9	2,9	4,3	7,0	9,9
	1,3	1,6	2,4	3,2	4,5	5,8
	1,2	1,5	2,1	2,8	3,7	4,6
	1,2	1,5	2,0	2,6	3,4	4,0
	1,1	1,4	1,9	2,4	3,1	3,7

-: 0,7;

-: 0,8;

-: 0,85;

-: 0,9;

+: 0,95.

I:

S: При коэффициенте Стьюдента равном 2,6 доверительная вероятность 0,95 может быть обеспечена при количестве измерений равном

n	p
0,7	0,8	0,9	0,95	0,98	0,99
	2,0	3,1	6,3	12,7	31,8	63,7
	1,3	1,9	2,9	4,3	7,0	9,9
	1,3	1,6	2,4	3,2	4,5	5,8
	1,2	1,5	2,1	2,8	3,7	4,6
	1,2	1,5	2,0	2,6	3,4	4,0
	1,1	1,4	1,9	2,4	3,1	3,7

-: 3;

-: 4;

-: 5;

+: 6;

-: 8.

I:

S: При многократных измерениях некоторой физической величины были получены следующие значения: 45; 44; 44; 46; 44; 126; 45. При этом среднее значение измеряемой величины равно

+: 45;

-: 44;

-: 56;

-: 60;

-: 72.

I:

S: При многократных измерениях некоторой физической величины были получены следующие значения: 10; 12; 11; 10; 12. При этом абсолютная погрешность первого измерения составила

+: 1;

-: 2;

-: 3;

-: 4;

-: 5.

I:

S: При статистической обработке данных измерений некоторой физической величины было получено ее среднее значение равное 12, а средняя абсолютная погрешность измерений составила 3. При этом относительная погрешность измерений составила

-: 15%;

-: 9%;

-: 36%;

+: 25%;

-: 40%.

I:

S: При статистической обработке данных измерений некоторой физической величины было получено ее среднее значение равное 12, а случайная погрешность измерений составила 2. При этом доверительный интервал составляет

-: От 2 до 12;

-: От 10 до 12;

+: От 10 до 14;

-: От 2 до 14;

-: От 0 до 12.

I:

S: Окончательная запись результатов измерений записана неверно в выражении

-: 284±1;

-: 350±38;

-: 52,7±0,3;

+: 284,5±1;

-: 4,750±0,006.

I:

S: По данным пяти измерений были получены следующие значения измеряемой величины: 40; 30; 30; 30; 30. При этом средняя арифметическая погрешность измерений составила

-: 2;

+: 3;

-: 4;

-: 5;

-: 6.

I:

S: По данным пяти измерений были получены следующие значения измеряемой величины: 40; 30; 30; 30; 30. При этом средняя квадратичная погрешность измерений составила

-: 1;

-: 2;

-: 3;

+: 4;

-: 5.

I:

S: По данным пяти измерений были получены следующие значения измеряемой величины: 40; 30; 30; 30; 30. При этом случайная погрешность измерений составила

-: 1;

-: 2;

-: 3;

-: 4;

+: 5.

I:

S: По данным пяти измерений были получены следующие значения измеряемой величины: 70; 70; 60; 60; 70. При этом средняя арифметическая погрешность измерений составила

-: 2;

-: 3;

-: 4;

+: 5;

-: 6.

I:

S: По формуле 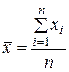рассчитывается

-: Средняя арифметическая погрешность;

+: Среднее арифметическое значение;

-: Средняя квадратичная погрешность измерения;

-: Абсолютная погрешность отдельного измерения;

-: Относительная погрешность.

I:

S: По формуле 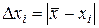рассчитывается

-: Средняя арифметическая погрешность;

-: Среднее арифметическое значение;

-: Средняя квадратичная погрешность измерения;

+: Абсолютная погрешность отдельного измерения

-: Относительная погрешность.

I:

S: По формуле 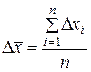рассчитывается

+: Средняя арифметическая погрешность;

-: Среднее арифметическое значение;

-: Средняя квадратичная погрешность измерения;

-: Абсолютная погрешность отдельного измерения

-: Относительная погрешность.

I:

S: По формуле 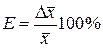рассчитывается

-: Средняя арифметическая погрешность;

-: Среднее арифметическое значение;

-: Средняя квадратичная погрешность измерения;

-: Абсолютная погрешность отдельного измерения

+: Относительная погрешность.

I:

S: По формуле 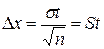рассчитывается

-: Средняя арифметическая погрешность;

-: Среднее арифметическое значение;

+: Случайная погрешность;

-: Абсолютная погрешность отдельного измерения

-: Относительная погрешность.

I:

S: По формуле 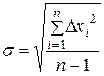рассчитывается

+: Средняя квадратичная погрешность измерения;

-: Среднее арифметическое значение;

-: Случайная погрешность;

-: Абсолютная погрешность отдельного измерения

-: Относительная погрешность.

V1: ЭФФЕКТ ДОПЛЕРА

I:

S: Эффект Доплера заключается в изменении:

-: скорости распространения волн, воспринимаемых наблюдателем, при относительном движения источника волн и наблюдателя

+: частоты волн, воспринимаемых наблюдателем, вследствие относительного движения источника волн и наблюдателя

-: громкости звука, воспринимаемого наблюдателем, вследствие относительного движения источника звука и приемника

-: интенсивности волн, воспринимаемых наблюдателем, вследствие относительного движения источника звука и приемника

-: фазы сигнала, воспринимаемого наблюдателем, вследствие относительного движения источника звука и приемника

I:

S: Эффект Доплера наблюдается:

-: только для ультразвука

-: только для света

-: только для звука

-: только для электромагнитных волн

+: для любых волн

I:

S: Эффект Доплера описывается выражением:

-:

-:

-:

-:

+:

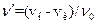
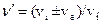
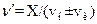
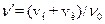
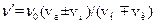
I:

S: В формуле для эффекта Доплера 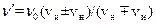символ ν₀ означает:

-: длину волны сигнала, испускаемого источником

-: скорость распространения сигнала в среде

+: частоту сигнала, испускаемого источником

-: скорость движения источника сигнала

-: амплитуду колебаний звуковой волны

I:

S: В гемодинамике УЗ эффект Доплера применяется для:

-: определения диаметра кровеносных сосудов

+: определения скорости кровотока

-: изучения распределения фармпрепаратов в организме человека

-: определения скорости оседания эритроцитов

-: визуализации внутренних органов человека

I:

S: В кардиологии УЗ эффект Доплера позволяет определить:

-: нарушения режима работы СА-узла

-: характер помех, возникающих при записи электрокардиограмм

-: изменение сечения аорты

-: визуализации желудочков сердца

+: клапанные нарушения сердца