Двумерный нормальный закон распределения случайной величины
Случайная величина (случайный вектор) 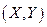 называется распределённой по
называется распределённой по
двумерному нормальному закону, если её совместная плотность имеет вид:
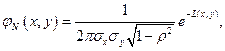
где
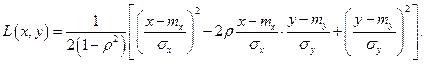
Числовые характеристики: 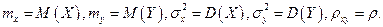
При этом одномерные случайные величины 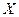 и
и 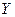 распределены нормально с параметрами соответственно
распределены нормально с параметрами соответственно 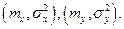 Условные законы распределения
Условные законы распределения 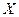 по
по 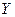 и
и 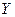 по
по 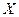 - также нормальные с числовыми характеристиками:
- также нормальные с числовыми характеристиками:
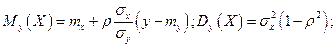
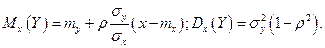
Из этих форму следует, что линии регрессии 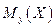 и
и 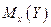 нормально распределённых случайных величин представляют собой прямые линии, т.е. нормальные регрессии
нормально распределённых случайных величин представляют собой прямые линии, т.е. нормальные регрессии 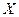 по
по 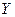 и
и 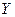 по
по 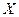 всегда линейны.
всегда линейны.
8. Понятие двумерного нормального закона для  мерной случайной величины
мерной случайной величины
Понятие двумерного нормального закона обобщается для любого натурального  .
.
Нормальный закон распределения  мерной случайной величины (
мерной случайной величины (  мерного случайного вектора)
мерного случайного вектора)  характеризуется параметрами, задаваемыми вектором средних
характеризуется параметрами, задаваемыми вектором средних 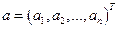 и ковариационной матрицей
и ковариационной матрицей 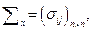 где
где 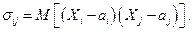 Ковариационная матрица и её определитель, называемый обобщённой дисперсией
Ковариационная матрица и её определитель, называемый обобщённой дисперсией  мерной случайной величины и характеризуют степень случайного разброса отдельно по каждой составляющей и в целом по
мерной случайной величины и характеризуют степень случайного разброса отдельно по каждой составляющей и в целом по  мерной величине.
мерной величине.
Предельные теоремы теории вероятности.
Закон больших чисел. Неравенство Чебышева
Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика А.Н. Колмогорова, совокупное действие большого числа случайных величин приводит (при некоторых весьма общих условиях) к результаты, почти не зависящему от случая. Другими словами:
Если случайная величина Х представляет собой сумму достаточно большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму бесконечно мало, то Х имеет распределение, близкое к нормальному.
Этот факт имеет очень важное значение на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов.
Рассмотрим дискретную случайную величину Х, заданную таблицей распределения:
| X | 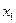 | 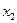 | … | 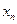 |
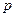 | 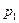 | 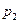 | … | 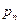 |
Требуется определить вероятность того, что отклонение значения случайной величины от ее математического ожидания будет не больше, чем заданное число  .
.
Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше чем 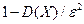 :
:
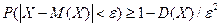 .
.
Теорема Чебышева
Теорема Чебышева. Если 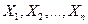 - попарно независимые случайные величины, причем дисперсии их равномерно ограничены, то для любого сколь угодно малого положительное число e, вероятность неравенства
- попарно независимые случайные величины, причем дисперсии их равномерно ограничены, то для любого сколь угодно малого положительное число e, вероятность неравенства
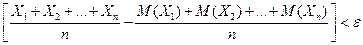
будет сколь угодно близка к единице, если число случайных величин достаточно велико, т.е.справедливо равенство:
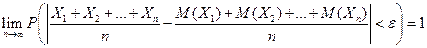 .
.
Иногда случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева упрощается:
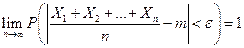 .
.
Дробь, входящая в записанное выше выражение является средним арифметическим возможных значений случайной величины.
Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.
Отклоняясь от математического ожидания, как в положительную, так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.
Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.
Теорема Бернулли
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равно р.
Теорема Бернулли. Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико.
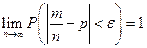
Здесь т – число появлений события А. Из приведённых выше утверждений вообще говоря не следует, что с увеличением число испытаний относительная частота неуклонно стремится к вероятности р, т.е. 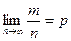 . В теореме имеется в виду только вероятность приближения относительной частоты к вероятности появления события А в каждом испытании.
. В теореме имеется в виду только вероятность приближения относительной частоты к вероятности появления события А в каждом испытании.
В случае, если вероятности появления события А в каждом опыте различны, то справедлива следующая теорема.
Теорема Пуассона. Если производится п независимых опытов и вероятность появления события А в каждом опыте равна 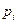 , то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей
, то при увеличении п частота события А сходится по вероятности к среднему арифметическому вероятностей 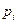 .
.
Замечание. Сформулированные утверждения остаются в силе и для непрерывных случайных величин.
