Условный оператор switch

В некоторых задачах программирования требуется выполнять проверку на равенство некоторой переменной константным значениям. Например, нужно преобразовать малые буквы в заглавные. В этом случае необходимо произвести проверку текущего символа со всеми возможными буквами алфавита и при равенстве с одной из них, заменить ее на заглавную. Для решения таких задач удобнее пользоваться условным оператором switch, который имеет следующий синтаксис:

switch expr
case case_expr,
<операторы1>
case {case_expr1, case_expr2, case_expr3,...}
<операторы2>
...
otherwise,
<операторы>
end

Здесь expr – переменная, значение которой проверяется на равенство тем или иным константам; case_expr – константы, с которым сравнивается значение переменной; otherwise – ключевое слово, для выполнения операторов, при всех ложных условиях.

Приведем пример работы данного оператора для преобразования малых букв латинского алфавита в заглавные.

function upper_symbol
ch='c';
switch ch
case 'a', ch='A';
case 'b', ch='B';
case 'c', ch='C';
case 'd', ch='D';
case 'e', ch='E';
...
case 'z', ch='Z';
end

disp(ch);

В данной программе задается символьная переменная ch со значением c. Затем, с помощью оператора switch проверяется ее значение со всеми возможными малыми буквами латинского алфавита от а до z. Как только одно из условий сработало, оператор switch завершает свою работу и выполнение программы переходит на функцию disp(), которая отображает значение переменной ch на экран.

Оператор цикла while

Язык программирования MatLab имеет два оператора цикла: while и for. С их помощью, например, выполняется программирование рекуррентных алгоритмов, подсчета суммы ряда, перебора элементов массива и многое другое.

В самом простом случае цикл в программе организуется с помощью оператора while, который имеет следующий синтаксис:

while <условие>
<операторы>
end

Здесь <условие> означает условное выражение подобное тому, которое применяется в операторе if, и цикл while работает до тех пор, пока это условие истинно.

Следует обратить внимание на то, что если условие будет ложным до начала выполнения цикла, то операторы, входящие в цикл, не будут выполнены ни разу.

Приведем пример работы цикла while для подсчета суммы ряда :

function sum_i
S = 0; % начальное значение суммы
i=1; % счетчик суммы
while i <= 20 % цикл (работает пока i <= 20)
S=S+i; % подсчитывается сумма
i=i+1; % увеличивается счетчик на 1
end % конец цикла
disp(S); % отображение суммы 210 на экране

Теперь усложним задачу и будем подсчитывать сумму ряда , пока . Здесь в операторе цикла получается два условия: либо счетчик по i доходит до 20, либо значение суммы S превысит 20. Данную логику можно реализовать с помощью составного условного выражения в операторе цикла while:

function sum_i
S = 0; % начальное значение суммы
i=1; % счетчик суммы
while i <= 20 & S <= 20 % цикл (работает пока i<=10 и S<=20
S=S+i; % подсчитывается сумма
i=i+1; % увеличивается счетчик на 1
end % конец цикла
disp(S); % отображение суммы 21 на экране

Приведенный пример показывает возможность использования составных условий в цикле while. В общем случае в качестве условного выражения можно записывать такие же условия, что и в условном операторе if.

Работу любого оператора цикла, в том числе и while, можно принудительно завершить с помощью оператора break. Например, предыдущую программу можно переписать следующим образом с использованием оператора break:

function sum_i
S = 0; % начальное значение суммы
i=1; % счетчик суммы
while i <= 20 % цикл (работает пока i<=10
S=S+i; % подсчитывается сумма
i=i+1; % увеличивается счетчик на 1
if S > 20 % если S > 20,
break; % то цикл завершается
end
end % конец цикла
disp(S); % отображение суммы 21 на экране

В данном примере второе условие завершения цикла, когда S будет больше 20, записано в самом цикле и с помощью оператора break осуществляется выход из цикла на функцию disp(), стоящую сразу после цикла while.

Второй оператор управления выполнением цикла continue позволяет пропускать выполнение фрагмента программы, стоящий после него. Например, требуется подсчитать сумму элементов массива

a = [1 2 3 4 5 6 7 8 9];

исключая элемент с индексом 5. Такую программу можно записать следующим образом:

function sum_array
S = 0; % начальное значение суммы
a = [1 2 3 4 5 6 7 8 9]; % массив
i=0; % счетчик индексов массива
while i < length(a) % цикл (работает пока i меньше
% длины массива а)
i=i+1; % увеличивается счетчик индексов на 1
if i == 5 % если индекс равен 5
continue; % то его не подсчитываем
end
S=S+a(i); % подсчитывается сумма элементов
end % конец цикла
disp(S); % отображение суммы 40 на экране

Следует отметить, что в данной программе увеличение индекса массива i происходит до проверки условия. Это сделано для того, чтобы значение индекса увеличивалось на 1 на каждой итерации работы цикла. Если увеличение счетчика i записать как в предыдущих примерах, т.е. после подсчета суммы, то из-за оператора continue его значение остановилось бы на 5 и цикл while работал бы «вечно».

Оператор цикла for

Часто при организации цикла требуется перебирать значение счетчика в заданном диапазоне значений и с заданным шагом изменения. Например, чтобы перебрать элементы вектора (массива), нужно организовать счетчик от 1 до N с шагом 1, где N – число элементов вектора. Чтобы вычислить сумму ряда, также задается счетчик от a до b с требуемым шагом изменения step. И так далее. В связи с тем, что подобные задачи часто встречаются в практике программирования, для их реализации был предложен свой оператор цикла for, который позволяет проще и нагляднее реализовывать цикл со счетчиком.

Синтаксис оператора цикла for имеет следующий вид:

for <счетчик> = <начальное значение>:<шаг>:<конечное значение>
<операторы цикла>
end

Рассмотрим работу данного цикла на примере реализации алгоритма поиска максимального значения элемента в векторе:

function search_max
a = [3 6 5 3 6 9 5 3 1 0];
m = a(1); % текущее максимальное значение
for i=1:length(a) % цикл от 1 до конца вектора с
% шагом 1 (по умолчанию)
if m < a(i) % если a(i) > m,
m = a(i); % то m = a(i)
end
end % конец цикла for
disp(m);

В данном примере цикл for задает счетчик i и меняет его значение от 1 до 10 с шагом 1. Обратите внимание, что если величина шага не указывается явно, то он берется по умолчанию равным 1.

В следующем примере рассмотрим реализацию алгоритма смещения элементов вектора вправо, т.е. предпоследний элемент ставится на место последнего, следующий – на место предпоследнего, и т.д. до первого элемента:

function queue
a = [3 6 5 3 6 9 5 3 1 0];
disp(a);
for i=length(a):-1:2 % цикл от 10 до 2 с шагом -1
a(i)=a(i-1); % смещаем элементы вектора а
end % конец цикла for
disp(a);

Результат работы программы

3 6 5 3 6 9 5 3 1 0
3 3 6 5 3 6 9 5 3 1

Приведенный пример показывает, что для реализации цикла со счетчиком от большего значения к меньшему, нужно явно указывать шаг, в данном случае, -1. Если этого не сделать, то цикл сразу завершит свою работу и программа будет работать некорректно.

В заключении рассмотрим работу оператора цикла for на примере моделирования случайной последовательности с законом изменения

,

где 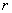- коэффициент от -1 до 1; 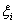- нормальная случайная величина с нулевым математическим ожиданием и дисперсией

,

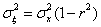где 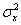- дисперсия моделируемого случайного процесса. При этом первый отсчет моделируется как нормальная случайная величина с нулевым математическим ожиданием и дисперсией 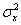. Программа моделирования имеет следующий вид:

function modeling_x
r = 0.95; % коэффициент модели
N = 100; % число моделируемых точек
ex = 100; % дисперсия процесса
et = ex*(1-r^2); % дисперсия случайной добавки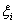
x = zeros(N,1); % инициализация вектора х
x(1) = sqrt(ex)*randn; % моделирование 1-го отсчета
for i=2:N % цикл от 2 до N
x(i)=r*x(i-1)+sqrt(et)*randn; % моделирование СП
end % конец цикла
plot(x); % отображение СП в виде графика

При выполнении данной программы будет показана реализация смоделированной случайной последовательности .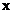

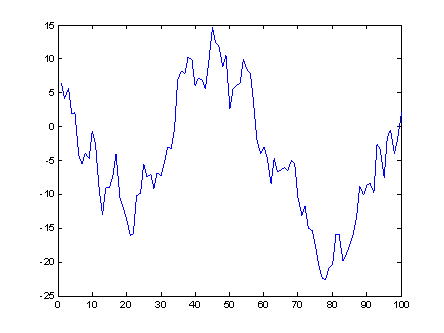
Рис. 2.1. Результат моделирования случайной последовательности.

Работа программы начинается с определения переменных 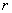, 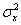(в программе переменная ex) и 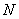для реализации указанной модели. Затем вычисляется дисперсия 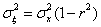и моделируется первый отсчет случайного процесса с помощью функции randn. Функция randn выполняет генерацию нормальных случайных величин с нулевым средним и единичной дисперсией. Чтобы сгенерировать случайную величину с дисперсией 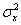достаточно случайную величину с единичной дисперсией умножить на 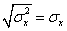, т.к. дисперсия – это средний квадрат случайной величины относительно математического ожидания. В результате имеем программную строчку

x(1) = sqrt(ex)*randn;

Затем, реализуется цикл for со счетчиком i от 2 до N с шагом 1. Внутри цикла выполняется моделирование оставшихся N-1 отсчетов случайного процесса в соответствии с приведенной выше формулой. В последней строчке программы записана функция plot(), которая выводит смоделированную последовательность на экран в виде графика. Более подробно работа с выводом графиков на экран будет рассмотрена в следующей главе.