Случай зависимой переменной

Пусть задана дифференцируемая функция 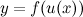. Тогда

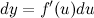
где 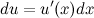в общем случае не является постоянной величиной. Поэтому дифференциал от функции 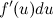берем как дифференциал от произведения

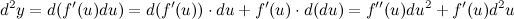
Пример

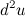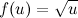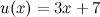Задание. Найти дифференциал второго порядка функции , где и - независимая переменная.

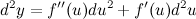
Найдем все необходимые компоненты формулы. Из условия имеем:

Из того, что 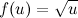и 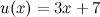, получаем:

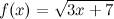
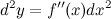
Решение.	Дифференциал пятого порядка вычисляется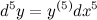

13 Вопрос. Правило Лопиталя, применение его к вычислению пределов. Примеры.

Правило Лопиталя

. Именно правила Лопиталя расправляются с пределами, в которых имеет место неопределённость 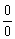или .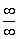

Первое правило Лопиталя

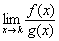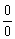, При этом: 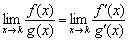, то есть при дифференцировании числителя и знаменателя значение предела не меняется.

!!!

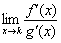
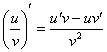И, в-третьих, «икс» может стремиться куда угодно, в том числе, к бесконечности – лишь бы была неопределённость .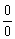

Вернёмся к Примеру 5 первой статьи о пределах, в котором был получен следующий результат:

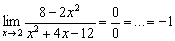
К неопределённости 0:0 применим первое правило Лопиталя:

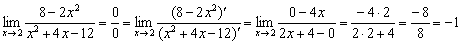
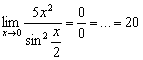
Применим правило Лопиталя:

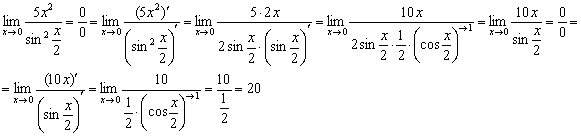
Второе правило Лопиталя

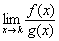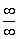, При этом: 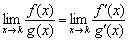, то есть при дифференцировании числителя и знаменателя значение предела не меняется.

Примечание: предел 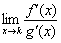должен существовать

Важно, чтобы была неопределённость .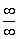

Проверим Пример №3 первого урока: 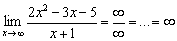. Используем второе правило Лопиталя:

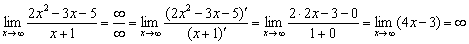
Пример 1

Вычислить предел

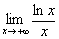
Получить ответ «обычными» методами непросто, поэтому для раскрытия неопределённости «бесконечность на бесконечность» используем правило Лопиталя:

Теорема

(Правило Лопиталя).

Пусть функци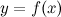и и 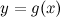удовлетворяют следующим условиям:

1) эти функции дифференцируемы в окрестности точки , кроме, может быть, самой точки ;

2) 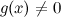и 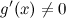в этой окрестности;

3) ;

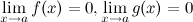4) 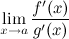существует конечный или бесконечный.

Тогда существует и 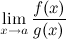, причем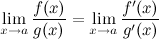

Таким образом, вычисление предела отношения двух функций может быть заменено при выполнении условий теоремы вычислением предела отношения производных этих функций.

Замечание

Правило Лопиталя распространяется на случай неопределенности типа при .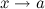

Применение правила Лопиталя на практике

Пример

Задание. Найти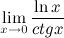

Решение. Получим неопределенность и для решения предела воспользуемся правилом Лопиталя.

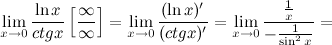
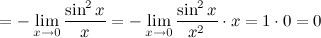
Ответ.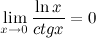

Замечание

Правило Лопиталя распространяется и на случай 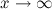. Чтобы убедится в этом, достаточно сделать замену 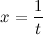и воспользоваться результатом выше приведенной теоремы.

Замечание

Иногда правило Лопиталя приходится применять несколько раз (делать несколько шагов), если от неопределенности не удается избавиться на первом шаге. Однако условия теоремы на каждом шаге должны оставаться справедливыми.

Замечание

правило Лопиталя работает только с неопределенностями и ,

14.Вопрос.Раскрытие неопределённостей различных видов.Примеры.