Оқиғалардың көбейтіндісі.

А және В оқиғаларының көбейтіндісі немесе қиылысуы деп, осы екі оқиғаның бірігіп пайда болуынан тұратын АВ оқиғасын атайды.

,

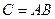немесе

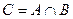деп белгіленеді.

Бірнеше оқиғалардың көбейтіндісі осы бойынша анықталады.

Мысалы.

A={жолаушы поездға билет сатып алды}, B={вагондағы өз орнына отырды}, C={поезд берілген вагонмен орнынан қозғалды}. Сонда

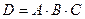={жолаушы кетіп қалды}.

Шартты ықтималдықтар.

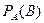шартты ықтималдығы депА оқиғасы пайда болды деп болжамдап есептелгендегі В оқиғасының ықтималдығын атайды.

Мысалы.

Урнада 3 ақ және 3 қара шар болды. Урнадағы шарларды екі рет бір-бірден кері орнына салмай шығарады. Егер бірінші тәжірибеде қара шар алып шыққан болса (А оқиғасы), екінші тәжірибеде ақ шар алып шығатындығының (В оқиғасы) ықтималдығын тап. Шешуі:

Бірінші тәжірибеден кейін урнада 5 шар қалды, олардың 3-уі ақ. Ізделінді шартты ықтималдық:

.

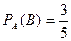Ықтималдықтарды көбейту теоремасы.

Ықтималдықтарды көбейту теоремасы. Екі оқиғаның бірігіп пайда болуының ықтималдығы – олардың біреуінің, бірінші оқиға пайда болды деп ойда есептеп алынған екіншісінің шартты ықтималдығына көбейткенге тең:

.

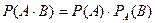А және В оқиғалары, екеуінің біреуінің ықтималдығы екіншісінің көрінуіне байланысты өзгермесе тәуелсіз деп аталады. Олай болмаған жағдайда олар тәуелді болар еді. Тәуелсіз оқиғаларға сонымен қатар В оқиғасының шартты ықтималдығы оның шартсыз ықтималдығына тең болатынын айтуға болады:

.

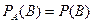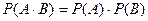
Тәуелсіз оқиғалары үшін көбейту теоремасы.

Йлесімді оқиғалардың ықтималдықтарының қосу теоремасы.

Екі оқиға, егер бір тәжірибеде біреуінің пайда болуы екіншісінің пайда болуын жоққа шығармаса үйлесімді деп аталады.

Мысалы.

Ойын сүйегін лақтырғанда, A – 4 ұпайдың пайда болуы, В – тақ санды ұпайдың пайда болуы. А және В оқиғалары – үйлесімді.

Теорема. Екі үйлесімді оқиғаның ең болмаса біреуінің көріну ықтималдығы осы ықтималдықтардың қосындысынан олардың ықтималдықтарының үйлесімді көрінуін шегергенге тең:

.

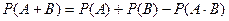Теорема. 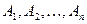жиынында тәуелсіз оқиғалардың ең болмаса біреуінің көріну ықтималдығы 1 мен қарама-қарсы оқиғалардың ықтималдықтарының көбейтіндісінің 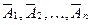, 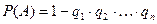айырмасына тең.

Егер 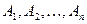оқиғаларының ықтималдықтары бірдей р –ға тең болса, онда бұл жағдайда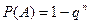

Мысалы:

Үш мерген нысанаға оқ атады. Бірінші мерген көздеген жерге оқ тию ықтималдығы 0,75 тең, екіншісінікі - 0,8, үшінсінікі - 0,9. а) үш мергеннің нысанаға тиюінің; б) ең болмаса бір мергеннің нысанаға тиюінің ықтималдығын тап.

Шешуі:

а)

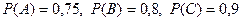
A, B, C оқиғалары тәуелсіз, онда тәуелсіз оқиғалардың көбейту теоремасы бойынша:

.

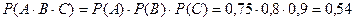б)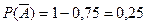

(1-ші мергеннің тимеуінің ықтималдығы)

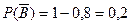(2-ші мергеннің тимеуінің ықтималдығы)

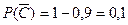(3-ші мергеннің тимеуінің ықтималдығы) яғни, , ,

.

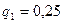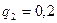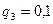
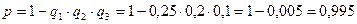Толық ықтималдық формуласы.