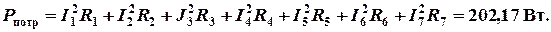Произвольно задать направление токов в ветвях исследуемой цепи.

2. Исходную цепь, содержащую n источников, преобразовать в n подсхем, каждая из которых содержит только один из источников, прочие источники исключаются следующим образом: источники напряжения замыкаются накоротко, а ветви с источниками тока обрываются. При этом необходимо помнить, что внутренние сопротивления реальных источников играют роль потребителей, и поэтому они должны оставаться в подсхемах.

Определить токи каждой из подсхем, задавшись их направлением в соответствии с полярностью источника, любым из известных методов. В большинстве случаев расчет ведется по закону Ома с использованием метода эквивалентных преобразований пассивных цепей.

4. Полный ток в любой ветви исходной цепи определяется как алгебраическая сумма токов вспомогательных подсхем, причем при суммировании со знаком «+» берутся токи подсхем, направление которых совпадает с направлением тока в исходной цепи, со знаком «–» – остальные.

Пример расчета

Задание

Рассчитать цепь, изображенную графом а, с параметрами: Е₁ = 20 В; Е₆ = 40 В; J₃ = 2А; R₁ = R₃ = R₅ = R₇ = 5,4 Ом; R₂ = R₄ = R₆ = 6,8 Ом.

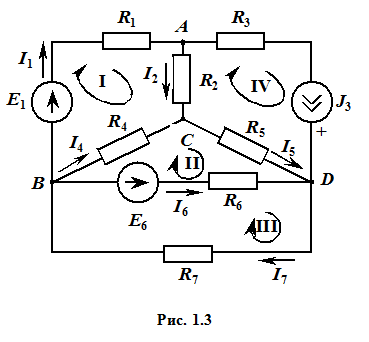
Подлежащая расчету цепь будет иметь вид (рис. 1.3).

1.4.2. Запись уравнений Кирхгофа

Для произвольно выбранных и обозначенных на схеме (см. рис. 1.3) положительных направлений токов ветвей и совокупности независимых контуров запишем:

– уравнения по I закону Кирхгофа:

для узла А: I₁ – I₂ – J₃ = 0,

для узла В: I₇ – I₆ – I₄ – I₁ = 0,

для узла С: I₄ + I₂ – I₅ = 0,

– уравнения по II закону Кирхгофа:

для контура I: I₁R₁ + I₂R₂ – I₄R₄ = E₁,

для контура II: I₄R₄ + I₅R₅ – I₆R₆ = –E₆,

для контура III: I₆R₆ + I₇R₇ = E₆,

для контура IV: J₃R₃ – I₅R₅ – I₂R₂ = U_J.

После подстановки численных значений коэффициентов получаем разрешимую систему уравнений с семью неизвестными величинами :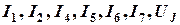

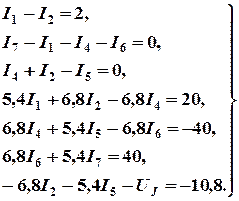
Метод контурных токов

Для рассматриваемой четырехконтурной цепи (см. рис. 1.3) система уравнений относительно контурных токов, совпадающих по направлению с обходом контуров, примет вид

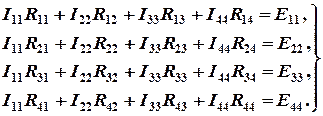
Для выбранных контурных токов I₄₄ = J₃. Подсчитаем значения коэффициентов системы:

– собственные сопротивления контуров:

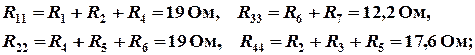
– общие сопротивления контуров:

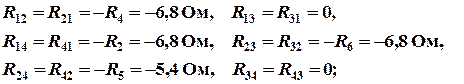
– контурные ЭДС:

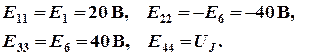
После подстановки численных значений коэффициентов и необходимых преобразований система уравнений примет вид

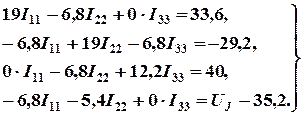
В случае решения данной системы при помощи определителей необходимо совместно решить систему из первых трех уравнений относительно неизвестных токов I₁₁, I₂₂, I₃₃, а затем из четвертого уравнения системы определить U_J.

Результаты расчета системы уравнений следующие:

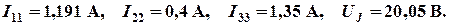
В соответствии с принятыми (см. рис. 1.3) положительными направлениями токов в ветвях вычисляем их значения:

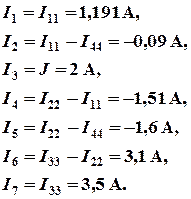
Баланс мощности

Мощность источников

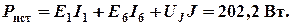
Мощность потребителей