Задания к контрольной работе. Методические рекомендации по написанию контрольных работ для студентов заочной формы обучения
Эконометрика
Методические рекомендации по написанию контрольных работ для студентов заочной формы обучения
САМАРА 2012
УДК 330.43(07)
ББК 65в6
Э-40
Эконометрика. Методические рекомендации по написанию контрольных работ для студентов заочной формы обучения. / Составитель Нестерова С.И. – Самара, МИР, 2012. - 25 с.
Рекомендации предназначены для студентов факультета экономики и менеджмента Международного института рынка, обучающихся по заочной форме специальностей «Финансы и кредит», «Маркетинг», «Прикладная информатика», «Менеджмент организации» и «Экономика и управление на предприятии».
СоставительНестерова С.И., к.э.н.
Печатается по решению
Учебно-методического совета
Международного института рынка
© Международный институт рынка, 2012
© Составление Нестерова С.И., 2012
Варианты контрольной работы
| № предприятия | Вариант 1 | Вариант 2 | Вариант 3 | ||||||
| Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на персонал (x2), тыс. руб. | Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на мерчендайзинг (x2), тыс. руб. | Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на мерчендайзинг (x2), тыс. руб. | |
| 1069,5 | 70,6 | 100,7 | 1411,7 | 91,8 | 137,0 | 114,9 | 6,9 | 4,6 | |
| 1138,5 | 75,8 | 93,6 | 1513,3 | 93,5 | 127,3 | 166,5 | 9,0 | 4,4 | |
| 1191,0 | 76,9 | 91,7 | 1602,4 | 97,0 | 121,6 | 221,4 | 9,2 | 4,9 | |
| 1240,5 | 90,0 | 84,8 | 1615,1 | 102,3 | 111,5 | 325,4 | 11,2 | 5,4 | |
| 1351,5 | 90,7 | 91,8 | 1687,5 | 103,7 | 120,9 | 383,1 | 11,6 | 5,9 | |
| 1389,0 | 90,8 | 96,5 | 1754,6 | 103,8 | 126,9 | 474,8 | 16,1 | 6,4 | |
| 1405,5 | 94,3 | 111,5 | 1818,9 | 123,7 | 132,6 | 497,8 | 16,7 | 7,6 | |
| 1474,5 | 95,0 | 75,7 | 1862,6 | 129,2 | 138,0 | 581,7 | 17,9 | 5,6 | |
| 1560,0 | 95,8 | 104,7 | 1799,0 | 137,0 | 142,5 | 683,7 | 18,6 | 7,9 | |
| 1591,5 | 96,3 | 103,3 | 1765,4 | 137,0 | 140,6 | 872,1 | 19,0 | 8,7 | |
| 1594,5 | 97,8 | 109,7 | 1812,3 | 138,0 | 143,1 | 889,8 | 20,5 | 10,0 | |
| 1597,5 | 99,3 | 112,8 | 1810,3 | 138,6 | 148,5 | 1015,2 | 22,2 | 11,0 | |
| 1599,0 | 100,4 | 112,9 | 1902,3 | 139,6 | 148,4 | 1222,8 | 22,7 | 13,4 | |
| 1621,5 | 102,2 | 100,2 | 2181,2 | 140,0 | 149,6 | 1247,0 | 24,1 | 12,0 | |
| 1689,0 | 104,3 | 105,0 | 2223,1 | 141,8 | 150,2 | 1342,6 | 25,1 | 13,1 | |
| 1699,5 | 104,6 | 100,4 | 2236,9 | 143,3 | 156,8 | 1391,8 | 25,4 | 12,8 | |
| 1794,0 | 105,5 | 115,7 | 2368,1 | 146,6 | 157,4 | 1582,2 | 26,4 | 20,5 | |
| 1818,0 | 113,5 | 116,1 | 2399,8 | 155,5 | 157,9 | 1640,1 | 30,5 | 20,6 | |
| 1944,0 | 123,6 | 110,0 | 2566,1 | 165,6 | 160,6 | 1976,0 | 34,9 | 20,8 | |
| 1969,5 | 141,3 | 115,3 | 2599,7 | 196,4 | 163,8 | 2145,2 | 41,1 | 22,4 |
| № предприятия | Вариант 4 | Вариант 5 | Вариант 6 | ||||||
| Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на мерчендайзинг (x2), тыс. руб. | Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на мерчендайзинг (x2), тыс. руб. | Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на мерчендайзинг (x2), тыс. руб. | |
| 822,5 | 6,9 | 284,6 | 657,4 | 29,1 | 180,5 | 1355,4 | 16,5 | 308,3 | |
| 905,0 | 9,0 | 269,9 | 726,2 | 39,1 | 173,4 | 1323,3 | 23,3 | 298,4 | |
| 975,4 | 9,2 | 266,8 | 787,0 | 40,6 | 173,4 | 1359,7 | 28,9 | 297,7 | |
| 1094,1 | 11,2 | 254,3 | 886,5 | 50,3 | 166,3 | 1337,0 | 36,4 | 292,2 | |
| 1219,3 | 11,6 | 296,2 | 988,2 | 52,5 | 196,0 | 1593,1 | 41,9 | 366,3 | |
| 1411,8 | 16,1 | 326,8 | 1157,8 | 75,0 | 226,8 | 1872,6 | 64,8 | 424,2 | |
| 1530,9 | 16,7 | 389,0 | 1256,7 | 78,6 | 271,2 | 2264,5 | 84,1 | 520,1 | |
| 1721,7 | 17,9 | 267,2 | 1425,2 | 85,5 | 187,6 | 1581,5 | 91,7 | 361,6 | |
| 2213,8 | 18,6 | 376,3 | 1834,9 | 89,6 | 270,5 | 2375,0 | 108,2 | 518,5 | |
| 2286,8 | 19,0 | 374,4 | 1900,7 | 91,9 | 274,5 | 2464,0 | 133,1 | 520,2 | |
| 2382,0 | 20,5 | 408,5 | 1981,2 | 99,3 | 308,4 | 2809,4 | 144,2 | 583,2 | |
| 2450,3 | 22,2 | 423,4 | 2038,6 | 107,8 | 322,7 | 3030,4 | 161,7 | 609,1 | |
| 3407,1 | 22,7 | 430,7 | 2854,0 | 119,8 | 329,6 | 3119,9 | 170,1 | 629,8 | |
| 3455,8 | 24,1 | 386,8 | 2915,5 | 128,7 | 297,2 | 2826,4 | 194,6 | 572,5 | |
| 3826,5 | 25,1 | 406,6 | 3231,8 | 134,7 | 322,4 | 3105,2 | 207,3 | 603,7 | |
| 3954,0 | 25,4 | 389,7 | 3346,0 | 136,7 | 311,5 | 3057,8 | 216,9 | 579,9 | |
| 4244,9 | 26,4 | 449,5 | 3607,6 | 143,0 | 360,7 | 3564,0 | 250,8 | 669,3 | |
| 4563,5 | 30,5 | 491,1 | 3901,1 | 170,2 | 396,3 | 3924,2 | 260,9 | 796,3 | |
| 5214,7 | 34,9 | 470,7 | 4501,3 | 206,0 | 381,4 | 3839,0 | 280,7 | 772,1 | |
| 5334,1 | 41,1 | 495,8 | 4633,7 | 243,1 | 401,8 | 4074,5 | 301,6 | 817,2 |
| № предприятия | Вариант 7 | Вариант 8 | Вариант 9 | ||||||
| Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на мерчендайзинг (x2), тыс. руб. | Товарооборот за месяц (y), тыс. руб. | Запасы на начало месяца, тыс. руб. | Затраты на мерчендайзинг (x2), тыс. руб. | Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на рекламу (x2), тыс. руб. | |
| 923,2 | 29,9 | 22,7 | 260,5 | 230,0 | 69,6 | 288,7 | 8,7 | 30,9 | |
| 989,0 | 34,4 | 22,0 | 287,5 | 241,6 | 70,3 | 314,4 | 10,1 | 32,2 | |
| 1040,5 | 37,4 | 22,0 | 306,1 | 246,0 | 71,5 | 334,7 | 11,2 | 39,1 | |
| 1091,3 | 53,2 | 20,6 | 326,9 | 250,6 | 70,9 | 352,2 | 16,1 | 36,9 | |
| 1197,9 | 54,3 | 22,9 | 361,8 | 257,9 | 91,5 | 387,5 | 16,9 | 42,8 | |
| 1250,2 | 56,5 | 25,9 | 388,0 | 261,3 | 114,1 | 404,7 | 17,7 | 40,6 | |
| 1267,9 | 60,3 | 31,5 | 396,6 | 274,5 | 146,8 | 446,9 | 19,2 | 83,8 | |
| 1350,3 | 84,3 | 22,0 | 429,2 | 279,4 | 105,1 | 481,5 | 30,2 | 58,6 | |
| 1438,1 | 85,1 | 30,8 | 462,7 | 281,3 | 152,5 | 515,3 | 27,5 | 87,2 | |
| 1468,2 | 90,9 | 30,9 | 473,8 | 290,6 | 155,8 | 527,7 | 29,4 | 90,0 | |
| 1486,1 | 94,8 | 33,1 | 480,7 | 298,6 | 176,1 | 537,6 | 30,7 | 98,0 | |
| 1502,5 | 97,9 | 35,0 | 486,4 | 301,2 | 189,0 | 558,7 | 34,5 | 109,8 | |
| 1511,4 | 105,0 | 35,3 | 532,7 | 304,6 | 197,0 | 595,2 | 37,4 | 118,4 | |
| 1536,5 | 114,2 | 31,9 | 547,9 | 321,6 | 182,0 | 606,1 | 40,9 | 107,8 | |
| 1605,6 | 117,7 | 33,8 | 575,4 | 330,6 | 194,2 | 634,4 | 42,3 | 119,3 | |
| 1616,7 | 123,2 | 32,4 | 581,0 | 321,8 | 187,1 | 649,2 | 50,6 | 116,8 | |
| 1706,7 | 126,8 | 37,4 | 617,4 | 345,6 | 216,5 | 704,6 | 47,1 | 136,1 | |
| 1730,8 | 137,6 | 37,6 | 643,7 | 348,7 | 257,8 | 732,3 | 54,2 | 110,3 | |
| 1874,3 | 154,4 | 38,8 | 738,1 | 349,0 | 272,2 | 801,7 | 60,9 | 156,4 | |
| 1902,3 | 190,0 | 41,1 | 750,4 | 350,6 | 291,4 | 826,5 | 75,1 | 174,0 |
| № предприятия | Вариант 10 | Вариант 11 | Вариант 12 | ||||||
| Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на содержание торговой точки (x2), тыс. руб. | Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на рекламу (x2), тыс. руб. | Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на рекламу (x2), тыс. руб. | |
| 680,0 | 7,5 | 96,0 | 331,4 | 26,2 | 79,0 | 1811,2 | 40,6 | 117,9 | |
| 755,6 | 8,8 | 100,6 | 644,7 | 33,2 | 84,6 | 2012,8 | 42,6 | 131,4 | |
| 811,7 | 9,8 | 124,3 | 880,2 | 44,6 | 102,4 | 2298,7 | 48,9 | 171,2 | |
| 880,0 | 14,1 | 118,8 | 1346,5 | 66,8 | 97,7 | 2559,1 | 51,4 | 196,6 | |
| 1041,8 | 14,9 | 138,2 | 1722,8 | 78,6 | 98,6 | 3081,5 | 50,7 | 230,8 | |
| 1142,1 | 15,9 | 131,4 | 2277,5 | 93,0 | 113,6 | 3583,7 | 62,4 | 227,6 | |
| 1299,2 | 17,3 | 271,3 | 2684,3 | 126,3 | 180,6 | 4356,3 | 59,7 | 482,0 | |
| 1416,4 | 27,7 | 206,6 | 3259,8 | 206,0 | 190,7 | 4795,2 | 54,2 | 468,4 | |
| 1543,6 | 25,3 | 311,0 | 3946,1 | 214,5 | 257,0 | 5452,7 | 68,5 | 697,1 | |
| 1593,8 | 27,1 | 322,4 | 5094,5 | 276,6 | 204,6 | 5745,4 | 100,3 | 764,5 | |
| 1668,2 | 28,6 | 352,2 | 5430,3 | 293,3 | 216,3 | 6068,1 | 98,8 | 855,0 | |
| 1747,6 | 32,5 | 397,3 | 6478,4 | 344,0 | 369,9 | 6549,6 | 103,6 | 974,6 | |
| 1892,1 | 35,4 | 440,3 | 8440,2 | 386,5 | 405,6 | 7631,0 | 112,3 | 1114,5 | |
| 1950,1 | 38,8 | 424,7 | 8747,8 | 456,1 | 421,6 | 8254,5 | 119,6 | 1084,7 | |
| 2047,6 | 40,2 | 470,8 | 9494,4 | 483,7 | 1041,1 | 8928,4 | 120,6 | 1212,0 | |
| 2099,9 | 48,2 | 461,5 | 10031,3 | 652,7 | 1036,4 | 9265,5 | 125,6 | 1237,8 | |
| 2281,0 | 44,8 | 546,6 | 11735,1 | 651,3 | 1281,4 | 10248,2 | 128,9 | 1472,2 | |
| 2581,3 | 51,6 | 455,4 | 13584,4 | 803,3 | 1109,5 | 11695,3 | 130,6 | 1203,6 | |
| 2859,0 | 58,7 | 661,6 | 16951,4 | 1111,2 | 1588,2 | 13308,2 | 111,3 | 1758,3 | |
| 2961,7 | 72,5 | 744,5 | 18818,1 | 1389,0 | 1844,4 | 13894,9 | 140,6 | 2105,8 |
Задания к контрольной работе
1. Определить параметры уравнения линейной множественной регрессии по методу наименьших квадратов. Дать экономическую интерпретацию параметрам уравнения.
2. Рассчитать парные коэффициенты корреляции.
3. Определить коэффициенты множественной корреляции и детерминации. Сделать вывод о тесноте связи результата с факторами и объясняемости вариации результата.
4. Оценить значимость уравнения множественной регрессии с помощью F-критерия Фишера при уровнях значимости 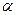 = 0,05 и
= 0,05 и 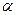 = 0,01. Сделать вывод.
= 0,01. Сделать вывод.
5. Получить уравнение регрессии в стандартизованном масштабе. Дать экономическую интерпретацию параметрам уравнения. Оценить информативность факторов на основе уравнения линейной регрессии в стандартизированном масштабе.
6. Рассчитать индексы множественной корреляции и детерминации для линейного уравнения регрессии в стандартизованном масштабе.
7. Проверить гипотезу о гомоскедастичности ряда остатков с уровнем значимости α = 0,05 (тест Голдфелда и Куандта).
8. Вычислить определитель матрицы межфакторной корреляции. Сделать вывод о взаимной коррелированности объясняющих переменных.
9. Выбрать наиболее значимый фактор.
10. Вычислить оценки коэффициентов однофакторной линейной модели (в качестве фактора принять наиболее значимый фактор) по методу наименьших квадратов. Дать экономическую интерпретацию коэффициента регрессии.
11. Определить коэффициенты корреляции и детерминации. Сделать вывод о тесноте связи результата с фактором и объясняемости вариации результата.
12. Рассчитать факторную, остаточную и общую дисперсии на одну степень свободы.
13. Оценить значимость уравнения линейной регрессии с помощью F-критерия Фишера при уровнях значимости 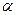 = 0,05 и
= 0,05 и 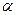 = 0,01. Сделать вывод.
= 0,01. Сделать вывод.
14. Определить стандартную ошибку коэффициента регрессии, оценить его значимость.
15. Найти доверительный интервал для коэффициента регрессии.
16. Определить стандартную ошибку параметра a, оценить его значимость.
17. Найти доверительный интервал для параметра a.
18. Сделать вывод о значимости линейного коэффициента корреляции.
Контрольная работа должна содержать разделы:
1. Описание задания;
2. Описание решения контрольной работы (по этапам);
3. Изложение полученных результатов.
Выполнение вычислений производится с помощью калькулятора или ПК. Запрещается использовать пакет анализа MS Excel, специализированные пакеты для статистического и эконометрического анализа данных. Все вычисления должны сопровождаться подробными объяснениями. При отсутствии хода решения ответ даже верный не засчитывается. Вычисления производятся с точностью до 4 знаков после запятой.
Образец решения
Задание
| Товарооборот за месяц (y), тыс. руб. | Площадь торгового зала (x1), кв м | Затраты на персонал (x2), тыс. руб. |
| 786,40 | 61,26 | 74,04 |
| 837,13 | 65,77 | 68,82 |
| 875,74 | 66,72 | 67,43 |
| 912,13 | 78,09 | 62,35 |
| 993,75 | 78,70 | 67,50 |
| 1021,32 | 78,78 | 70,96 |
| 1033,46 | 81,82 | 81,99 |
| 1084,19 | 82,43 | 55,66 |
| 1147,06 | 83,12 | 76,99 |
| 1170,22 | 83,55 | 75,96 |
| 1172,43 | 84,86 | 80,66 |
| 1174,63 | 86,16 | 82,94 |
| 1175,74 | 87,11 | 83,01 |
| 1192,28 | 88,67 | 73,68 |
| 1241,91 | 90,50 | 77,21 |
| 1249,63 | 90,76 | 73,82 |
| 1319,12 | 91,54 | 85,07 |
| 1336,76 | 98,48 | 85,37 |
| 1429,41 | 107,24 | 80,88 |
| 1448,16 | 122,60 | 84,78 |
Решение
В нашем случае зависимость товарооборота за месяц характеризуется следующим уравнением:
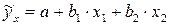 .
.
Параметры уравнения множественной регрессии оцениваются методом наименьших квадратов. Система нормальных уравнений имеет вид:
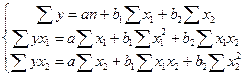 .
.
Для того чтобы получить систему нормальных уравнений, составим таблицу 1.
Таблица 1 – Исходные и расчетные данные для примера построения множественной регрессии
| n | x1 | x2 | y | x12 | x22 | y2 | yx1 | yx2 | x1x2 |
| 61,26 | 74,04 | 786,40 | 3752,28 | 5482,53 | 618420,33 | 48171,45 | 58228,08 | 4535,64 | |
| 65,77 | 68,82 | 837,13 | 4325,38 | 4736,68 | 700790,58 | 55056,23 | 57614,40 | 4526,36 | |
| 66,72 | 67,43 | 875,74 | 4451,83 | 4546,33 | 766912,31 | 58430,86 | 59047,74 | 4498,83 | |
| 78,09 | 62,35 | 912,13 | 6097,77 | 3887,89 | 831985,43 | 71226,81 | 56874,13 | 4869,03 | |
| 78,70 | 67,50 | 993,75 | 6193,00 | 4556,25 | 987539,06 | 78203,74 | 67078,13 | 5311,95 | |
| 78,78 | 70,96 | 1021,32 | 6206,66 | 5034,74 | 1043101,75 | 80462,27 | 72468,91 | 5590,07 | |
| 81,82 | 81,99 | 1033,46 | 6694,37 | 6721,59 | 1068031,06 | 84556,45 | 84728,18 | 6707,96 | |
| 82,43 | 55,66 | 1084,19 | 6794,12 | 3098,23 | 1175470,51 | 89366,05 | 60347,99 | 4588,00 | |
| 83,12 | 76,99 | 1147,06 | 6909,03 | 5926,74 | 1315743,94 | 95344,20 | 88306,66 | 6399,06 | |
| 83,55 | 75,96 | 1170,22 | 6981,34 | 5769,30 | 1369416,23 | 97777,09 | 88885,14 | 6346,45 | |
| 84,86 | 80,66 | 1172,43 | 7200,52 | 6506,32 | 1374583,83 | 99487,28 | 94569,99 | 6844,63 | |
| 86,16 | 82,94 | 1174,63 | 7423,09 | 6879,24 | 1379761,16 | 101203,21 | 97425,39 | 7145,99 | |
| 87,11 | 83,01 | 1175,74 | 7588,46 | 6891,44 | 1382353,48 | 102420,38 | 97603,32 | 7231,56 | |
| 88,67 | 73,68 | 1192,28 | 7862,99 | 5428,22 | 1421530,20 | 105723,62 | 87842,94 | 6533,15 | |
| 90,50 | 77,21 | 1241,91 | 8189,45 | 5960,75 | 1542344,83 | 112387,54 | 95882,89 | 6986,79 | |
| 90,76 | 73,82 | 1249,63 | 8236,63 | 5449,91 | 1561581,02 | 113411,49 | 92252,27 | 6699,92 | |
| 91,54 | 85,07 | 1319,12 | 8378,98 | 7237,51 | 1740071,37 | 120747,76 | 112221,99 | 7787,36 | |
| 98,48 | 85,37 | 1336,76 | 9697,90 | 7287,64 | 1786939,88 | 131641,84 | 114116,46 | 8406,83 | |
| 107,24 | 80,88 | 1429,41 | 11500,67 | 6541,96 | 2043217,99 | 153291,80 | 115614,19 | 8673,92 | |
| 122,60 | 84,78 | 1448,16 | 15030,40 | 7187,55 | 2097172,50 | 177542,50 | 122774,30 | 10393,83 | |
| Итого | 1708,14 | 1509,12 | 22601,47 | 149514,89 | 115130,80 | 26206967,45 | 1976452,57 | 1723883,11 | 130077,34 |
Итак, система нормальных уравнений имеет вид
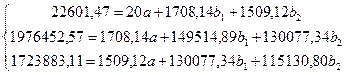
Решим эту систему по методу Крамера. Вычисляем определитель системы:
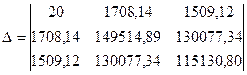 = 63116109,08.
= 63116109,08.
Аналогично вычисляем частные определители, заменяя соответствующий столбец столбцом свободных членов:
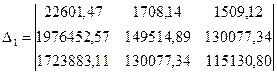 = -8788430890,31;
= -8788430890,31;
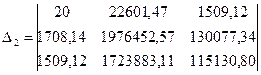 = 722640789,19;
= 722640789,19;
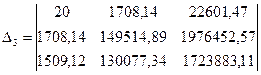 = 243795572,83.
= 243795572,83.
Коэффициенты уравнения определяются по формулам:
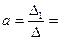 -8788430890,31/63116109,08 = -139,24;
-8788430890,31/63116109,08 = -139,24;
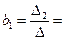 722640789,19/63116109,08 = 11,45;
722640789,19/63116109,08 = 11,45;
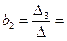 243795572,83/63116109,08 = 3,86.
243795572,83/63116109,08 = 3,86.
Таким образом, уравнение имеет вид: 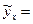 -139,24 + 11,45 х1 + 3,86 х2.
-139,24 + 11,45 х1 + 3,86 х2.
Экономическая интерпретация параметров уравнения: с увеличением площади торгового зала на 1 кв.м и неизменных затратах на персонал товарооборот в среднем увеличивается на 11,45 тыс. руб. При неизменной площади торгового зала и увеличении затрат на персонал на 1 тыс.руб. товарооборот в среднем увеличивается на 3,86 тыс.руб.
Определим парные коэффициенты корреляции 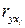 и
и 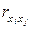 .
.
При этом воспользуемся следующими формулами:
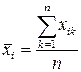 , , 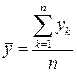 , , 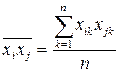 , , 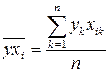 , , 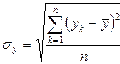 , , 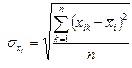 . В нашем случае . В нашем случае | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Для расчета Таблица 2 – Вспомогательная таблица для расчета
Теперь определим парные коэффициенты корреляции.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Подставив в уравнение регрессии значения х1 и х2, получим теоретические значения y, т.е. Таблица 3 – Расчет индекса множественной корреляции
Для вычисления индекса множественной корреляции воспользуемся следующей формулой
В нашем случае индекс множественной корреляции составит
Тогда Вывод о тесноте связи результата с факторами и объясняемости вариации результата: согласно шкале Чеддока теснота связи между товарооборотом, затратами на персонал и площадью торгового зала весьма высокая, т.е. затраты на персонал и площадь торгового зала – одни из главных факторов, от которых зависит размер товарооборота. Значение коэффициента детерминации свидетельствует о том, что товарооборот на 90% зависит от факторов, включенных в модель (затрат на персонал и площади торгового зала), и на 10% - от прочих факторов, не включенных в модель. Значимость уравнения множественной регрессии в целом оценивается с помощью с помощью F-критерия Фишера:
где R - индекс множественной корреляции (тоже, что и n - число наблюдений; m - число параметров при переменных х (в линейной регрессии совпадает с числом включенных в модель факторов). В нашем случае По таблице определяем Вывод: поскольку табличное значение критерия Фишера меньше расчетного, уравнение регрессии статистически значимо. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Уравнение регрессии в стандартизованном масштабе строится на основе матрицы парных коэффициентов корреляции:
где
Применяя МНК к уравнению множественной регрессии в стандартизованном масштабе, после соответствующих преобразований получим систему нормальных уравнений вида для определения стандартизованных коэффициентов регрессии.
|
В нашем случае система нормальных уравнений имеет вид:
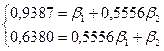
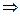
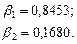
Окончательно получаем уравнение регрессии в стандартизованном масштабе в виде:
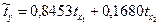 .
.
Из уравнения регрессии в стандартизованном масштабе можно сделать вывод, что площадь торгового зала является более значимым фактором, чем затраты на персонал, поскольку 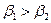 .
.
Рассчитаем индексы множественной корреляции и детерминации для линейного уравнения регрессии в стандартизованном масштабе.
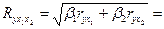
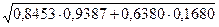 = 0,9490.
= 0,9490.
Сравниваем индекс множественной корреляции с парными индексами корреляции:
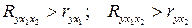 .
.
Следовательно, включение обоих факторов в уравнение множественной регрессии является обоснованным.
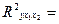 0,9007.
0,9007.
Гомоскедастичность остатков означает, что дисперсия каждого отклонения одинакова для всех значений x. Если это условие не соблюдается, то имеет место гетероскедастичность.
Применим тест Гольдфельда и Куандта (табл. 4). В нашем случае число объясняющих переменных k = 2, количество исходных данных в выборке n = 20. Упорядочим наблюдения по убыванию независимой переменной х1, относительно которой есть подозрение на гетероскедастичность. Опустим 4 наблюдения, оказавшихся в центре, т.е. v = 4. При значении v = 4 получим суммы квадратов остатков от первой и второй регрессии соответственно е1 = 12075,91 и е2 = 8891,33. Статистика Q = е1 / е2 = 12075,91 / 8891,33 = 1,36 удовлетворяет F-распределению с (6;6) степенями свободы.
Вывод: поскольку Q < Fтабл., гипотеза об однородности выборочной дисперсии принимается. Гомоскедастичность доказана.
Таблица 4 – Проверка регрессии на гетероскедастичность
| № | x1 | x2 | y | 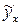 | е |
Первая группа с первыми 8 значениями: 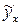 = 354,42+6,97х1+3,33х2 = 354,42+6,97х1+3,33х2 | |||||
| 122,60 | 84,78 | 1448,16 | 1491,08 | 1841,78 | |
| 107,24 | 80,88 | 1429,41 | 1371,07 | 3403,48 | |
| 98,48 | 85,37 | 1336,76 | 1324,93 | 140,12 | |
| 91,54 | 85,07 | 1319,12 | 1275,57 | 1896,21 | |
| 90,76 | 73,82 | 1249,63 | 1232,68 | 287,34 | |
| 90,50 | 77,21 | 1241,91 | 1242,13 | 0,05 | |
| 88,67 | 73,68 | 1192,28 | 1217,68 | 645,13 | |
| 87,11 | 83,01 | 1175,74 | 1237,88 | 3861,81 | |
| Итого | 12075,91 | ||||
Вторая группа со вторыми 8 значениями: 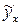 = 59,53+12,02х1-0,12х2 = 59,53+12,02х1-0,12х2 | |||||
| 82,43 | 55,66 | 1084,19 | 1043,57 | 1650,06 | |
| 81,82 | 81,99 | 1033,46 | 1033,02 | 0,19 | |
| 78,78 | 70,96 | 1021,32 | 997,88 | 549,82 | |
| 78,70 | 67,50 | 993,75 | 997,26 | 12,31 | |
| 78,09 | 62,35 | 912,13 | 990,59 | 6155,89 | |
| 66,72 | 67,43 | 875,74 | 853,33 | 502,22 | |
| 65,77 | 68,82 | 837,13 | 841,68 | 20,67 | |
| 61,26 | 74,04 | 786,40 | 786,80 | 0,16 | |
| Итого | 8891,33 |
Коэффициент автокорреляции остатков находим по следующим рядам данных:
| n | 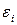 | 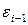 | 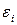 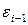 |
| -42,47 | -61,71 | 2620,56 | |
| -9,39 | -42,47 | 398,93 | |
| -83,54 | -9,39 | 784,74 | |
| -28,75 | -83,54 | 2401,90 | |
| -15,52 | -28,75 | 446,30 | |
| -80,76 | -15,52 | 1253,56 | |
| 64,70 | -80,76 | -5225,16 | |
| 37,25 | 64,70 | 2410,28 | |
| 59,42 | 37,25 | 2213,81 | |
| 28,55 | 59,42 | 1696,73 | |
| 7,05 | 28,55 | 201,38 | |
| -3,06 | 7,05 | -21,55 | |
| 31,68 | -3,06 | -96,80 | |
| 46,82 | 31,68 | 1483,00 | |
| 64,62 | 46,82 | 3025,25 | |
| 81,71 | 64,62 | 5280,20 | |
| 18,75 | 81,71 | 1532,02 | |
| 28,39 | 18,75 | 532,25 | |
| -143,75 | 28,39 | -4080,68 | |
| Итого | 61,71 | 143,75 | 16856,73 |
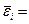 61,71/19 = 3,25;
61,71/19 = 3,25;
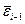 = 143,75/19 = 7,57;
= 143,75/19 = 7,57;
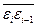 = 16856,73/19 = 887,20;
= 16856,73/19 = 887,20;
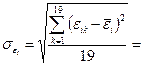
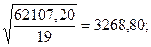
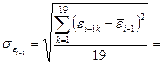
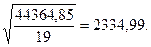
Отсюда находим
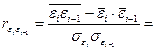
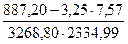 = 0,0001.
= 0,0001.
Вывод: коэффициент корреляции мал, его можно считать приемлемым. Автокорреляции остатков отсутствует.
Матрица парных коэффициентов корреляции в нашем случае имеет вид:
| y | х1 | х2 | |
| y | 0,9387 | 0,6380 | |
| х1 | 0,9387 | 0,5556 | |
| х2 | 0,6380 | 0,5556 |
Определитель матрицы парных коэффициентов регрессии составляет
Det |R| = 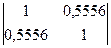 = 0,6908.
= 0,6908.
Вывод: значение определителя близко к единице, что свидетельствует о слабой взаимной коррелированности объясняющих переменных.
Наиболее значимый фактор – это площадь торгового зала, т.к. ryx1 > ryx2.
Предположим, что зависимость товарооборота за месяц характеризуется уравнением 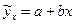 .
.
Параметры a и b найдем из следующей системы уравнений
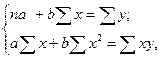 |
где n – число наблюдений.
Расчет производных данных для корреляционного анализа произведем в таблице 5.
Таблица 5 – Расчет производных данных для корреляционного анализа
| n | x | y | xy | x2 | y2 |
| 61,26 | 786,40 | 48171,45 | 3752,28 | 618420,33 | |
| 65,77 | 837,13 | 55056,23 | 4325,38 | 700790,58 | |
| 66,72 | 875,74 | 58430,86 | 4451,83 | 766912,31 | |
| 78,09 | 912,13 | 71226,81 | 6097,77 | 831985,43 | |
| 78,70 | 993,75 | 78203,74 | 6193,00 | 987539,06 | |
| 78,78 | 1021,32 | 80462,27 | 6206,66 | 1043101,75 | |
| 81,82 | 1033,46 | 84556,45 | 6694,37 | 1068031,06 | |
| 82,43 | 1084,19 | 89366,05 | 6794,12 | 1175470,51 | |
| 83,12 | 1147,06 | 95344,20 | 6909,03 | 1315743,94 | |
| 83,55 | 1170,22 | 97777,09 | 6981,34 | 1369416,23 | |
| 84,86 | 1172,43 | 99487,28 | 7200,52 | 1374583,83 | |
| 86,16 | 1174,63 | 101203,21 | 7423,09 | 1379761,16 | |
| 87,11 | 1175,74 | 102420,38 | 7588,46 | 1382353,48 | |
| 88,67 | 1192,28 | 105723,62 | 7862,99 | 1421530,20 | |
| 90,50 | 1241,91 | 112387,54 | 8189,45 | 1542344,83 | |
| 90,76 | 1249,63 | 113411,49 | 8236,63 | 1561581,02 | |
| 91,54 | 1319,12 | 120747,76 | 8378,98 | 1740071,37 | |
| 98,48 | 1336,76 | 131641,84 | 9697,90 | 1786939,88 | |
| 107,24 | 1429,41 | 153291,80 | 11500,67 | 2043217,99 | |
| 122,60 | 1448,16 | 177542,50 | 15030,40 | 2097172,50 | |
| Итого | 1708,14 | 22601,47 | 1976452,57 | 149514,89 | 26206967,45 |
Подставим полученные значения в систему уравнений и получим:
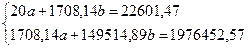
Из системы находим, что a = 44,17, b = 12,71.
Уравнение регрессии имеет вид 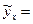 44,17 + 12,71х.
44,17 + 12,71х.
Экономическая интерпретация коэффициента регрессии: с увеличением площади торгового зала на 1 кв.м товарооборот увеличится в среднем на 12,71 тыс.руб.
Найдем коэффициент корреляции
rxy = 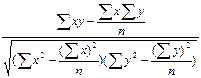 =
=
= 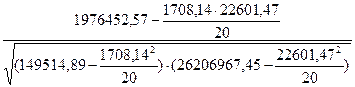 = 0,9387.
= 0,9387.
Вывод по коэффициенту корреляции: согласно шкале Чеддока теснота связи между товарооборотом и площадью торгового зала весьма высокая.
Возведем коэффициент корреляции в квадрат, получим коэффициент детерминации, равный 0,8812, откуда можно сделать вывод о том, что товарооборот на 88,12% зависит от площади торгового зала и на 11,88% - от прочих факторов, не включенных в модель.
Для оценки значимости уравнения регрессии составим вспомогательную таблицу 6.
Таблица 6 – Вспомогательная таблица для оценки значимости уравнения регрессии

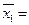 85,41;
85,41;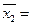 75,46;
75,46;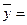 1130,07;
1130,07;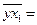 98822,63;
98822,63;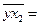 86194,16;
86194,16;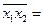 6503,87.
6503,87.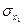 ,
, 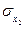 и
и 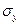 составим вспомогательную таблицу 2.
составим вспомогательную таблицу 2.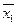 )2
)2 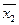 )2
)2 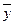 )2
)2 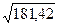 = 13,47;
= 13,47;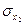 =
= 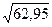 = 7,93;
= 7,93;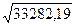 = 182,43.
= 182,43.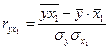 =
= 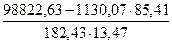 = 0,9387;
= 0,9387;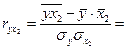
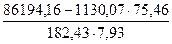 = 0,6380;
= 0,6380;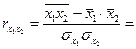
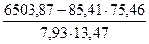 = 0,5556.
= 0,5556. , а также
, а также  = y -
= y - 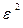 (табл. 3).
(табл. 3).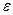
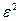
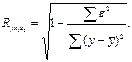
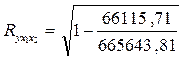 = 0,9490;
= 0,9490;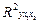 = 0,94902 = 0,9007.
= 0,94902 = 0,9007.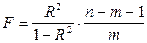 ,
, 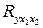 );
);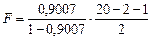 = 77,07.
= 77,07.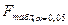 , которое составляет 3,59.
, которое составляет 3,59.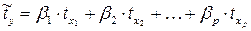 ,
, 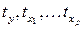 - стандартизованные переменные:
- стандартизованные переменные: 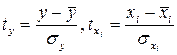 , для которых среднее значение равно нулю, а среднее квадратическое значение равно единице;
, для которых среднее значение равно нулю, а среднее квадратическое значение равно единице;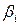 - стандартизованные коэффициенты регрессии.
- стандартизованные коэффициенты регрессии.