Этапы статистического исследования. Собранные в процессе первой стадии статистического исследования – статистического наблюдения – данные о величине какого-либо признака изучаемой совокупности

Собранные в процессе первой стадии статистического исследования – статистического наблюдения – данные о величине какого-либо признака изучаемой совокупности должны быть обработаны так, чтобы получился точный и обстоятельный ответ на все вопросы, поставленные целью исследования. Задача второй стадии статистического исследования – статистической обработки (сводки) – состоит в том, чтобы упорядочить и обобщить первичный материал, свести его в группы и на этой основе дать обобщенную характеристику совокупности. Качество исходного статистического материала предопределяет качество обобщающих показателей, полученных в результате статистической сводки.

Различают сводку простую и сложную (статистическую группировку).

Простая сводка – это операция по подсчету общих итогов по совокупности единиц наблюдения. Сложная сводка – это комплекс операций, включающих группировку единиц наблюдения, подсчет итогов по каждой группе и по всей совокупности и представление результатов сводки и группировки в виде статистических таблиц.

Статистическая группировка сводится к расчленению совокупности на группы по отобранному существенному для единиц совокупности признаку (группировочному признаку). Выбор группировочного признака, т.е. признака, по которому производится объединение единиц исследуемой совокупности в группы, – один из самых существенных и сложных вопросов теории группировки и статистического исследования. От правильного выбора группировочного признака часто зависят результаты всего статистического исследования. Группировка позволяет получить такие результаты, по которым можно выявить состав совокупности, характерные черты и свойства типичных явлений, обнаружить закономерности и взаимосвязи.

Наиболее простым и часто используемым способом обобщения статистических данных являются ряды распределения. Статистическим рядом (законом) распределения называют численное распределение единиц совокупности по изучаемому признаку. Пусть некоторая СВ является дискретной, т.е. может принимать лишь фиксированные (на некоторой шкале) значения X_i. В этом случае ряд значений вероятностей P(X_i) для всех (i=1, 2, …, n) допустимых значений этой величины называют её законом распределения.

В зависимости от используемого группировочного признака статистические ряды могут быть атрибутивными и вариационными (количественными).

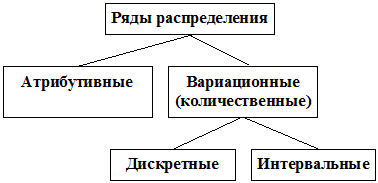
Атрибутивные ряды распределения отражают качественное состояние единиц совокупности (пол человека, семейное положение, отраслевую принадлежность предприятия, его форму собственности и т.д.), а вариационные – имеют числовое выражение (объем производства, доход семьи, возраст человека, балл успеваемости и т.д.).

Примером атрибутивного ряда может служить распределение студентов группы по полу.

Группы студентов по полу	Число студентов, чел.	Удельный вес в общей численности студентов, %
Женщины		83.3
Мужчины		16.7
Всего		100.0

Вариационные (количественные) группированные ряды могут быть дискретными или интервальными. Дискретный вариационный ряд распределения – это ряд, в котором численное распределение единиц совокупности по дискретному признаку выражено целым конечным значением. Примером может служить распределение рабочих по разрядам, распределение семей города по числу детей и т.п. Интервальный ряд распределения – это ряд, в котором значения признака заданы в виде интервала. Построение интервальных вариационных рядов целесообразно прежде всего для случайных величин, характеризующихся непрерывной вариацией признака (т.е. когда величина признака у единиц совокупности может принимать любые значения, хотя бы и в определенных пределах).

Итак, закон распределения вероятностей дискретной СВ несет в себе всю информацию о ней. Этот закон (или просто – распределение случайной величины) можно задать тремя способами:

- в виде таблицы значений величины и соответствующих им вероятностей;

- в виде диаграммы или, как ее иногда называют, гистограммы распределения;

- в виде формулы, например, для нормального, биномиального и пр. распределения.