Цепь переменного тока с емкостью

Емкостное сопротивление. Сопротивление, которое оказывает емкость переменному току, называют емкостным. Оно обозначается X_с и измеряется в омах. Физически емкостное сопротивление обусловлено действием э. д. с. е_с, возникающей в конденсаторе С. Эта э. д. с. направлена против приложенного напряжения u, так как заряженный конденсатор можно рассматривать как источник с некоторой э. д. с. е_с, действующей между его пластинами. Поэтому э. д. с. е_с препятствует изменению тока под действием напряжения u, т. е. оказывает прохождению переменного тока определенное сопротивление.

Из формулы (70) следует, что чем больше емкость С и скорость изменения напряжения ?u/?t, т. е. частота его изменения f (значение ?), тем больше ток i в цепи с емкостью и тем меньше емкостное сопротивление:

X_с= 1 /(?C)

Закон Ома для цепи с емкостью:

I = U / X_с= U / ( 1 /(?C) )

Если в цепь постоянного тока включить конденсатор (идеальный – без потерь), то в течение короткого времени после включения по цепи потечет зарядный ток. После того как конденсатор зарядится до напряжения, соответствующего напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи или бесконечно большое сопротивление.

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. Если включить конденсатор к переменному напряжению сети, то в течение первой четверти периода, когда напряжение сети будет возрастать (рисунок 1), конденсатор будет заряжаться.

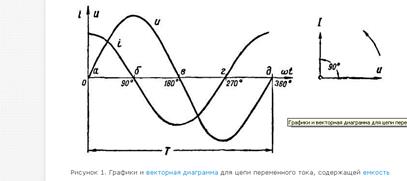
Рисунок 1. Графики и векторная диаграмма для цепи переменного тока, содержащей емкость

По мере накопления зарядов на обкладках конденсатора напряжение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимума, заряд конденсатора прекращается и ток в цепи становится равным нулю.

Ток в цепи конденсатора можно определить по формуле:

где q – количество электричества, протекающее по цепи.

Из электростатики известно:

q = C × u_C = C × u ,

где C – емкость конденсатора; u – напряжение сети; u_C – напряжение на обкладках конденсатора.

Окончательно для тока имеем:

Из последнего выражения видно, что, когда максимально (положения а, в, д), i также максимально. Когда (положения б, г на рисунке 1), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшаться, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное. В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд. Из рисунка 1 видно, что ток в цепи с емкостью в своих изменениях опережает по фазе на 90° напряжение на обкладках конденсатора.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Поскольку мы отметили выше, что скорость изменения тока пропорциональна угловой частоте ω, из формулы

получаем аналогично, что скорость изменения напряжения также пропорциональна угловой частоте ω и для действующего значения тока имеем

I = 2 × π × f × C × U .

Обозначая , где x_C называется емкостным сопротивлением, или реактивным сопротивлением емкости. Итак мы получили формулу емкостного сопротивления при включении емкости в цепи переменного тока. Отсюда, на основании выражения закона Ома, мы можем получить ток для цепи переменного тока, содержащей емкость:

Напряжение на обкладках конденсатора

U_C = I_C × x_C .

Та часть напряжения сети, которая имеется на конденсаторе, называется емкостнымпадением напряжения, или реактивной слагающей напряжения, и обозначается U_C.

Емкостное сопротивление x_C, так же как индуктивное сопротивление x_L, зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет уменьшаться.