Приложение 1. Конечномерные линейные пространства

Вводные сведения.

Множества. Обозначаем множество объектов , представляющих собой последовательность вещественных или комплексных чисел . В первом случае - вещественных, во втором – комплексных последовательностей. Объекты этого множества можно покомпонентно складывать по правилу: , получая новый элемент того же класса. Элементы из можно умножать на вещественное или комплексное число , по правилу: , вновь получая элемент того же класса. Таким образом, образует 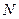- мерное линейное пространство, поскольку вместе с любыми своими элементами содержит и их линейные комбинации. Индексы, нумерующие компоненты объекта , могут располагаться внизу, как это записано выше, либо вверху. Различие между двумя этими случаями, конечно, есть, но оно появляется в вопросах не связанных с рассматриваемыми в этой книге. Не следует также спешить и называть линейное пространство векторным или Евклидовым – понятия наверняка известные читателю. Дело в том, что вектора – это более частные и, в какой-то мере, сложные объекты, чем введенные элементы из , хотя они и представляются своими координатами, как элементами из . Например, вектора имеют такую операцию, как векторное умножение, которой нет в . Еще, и это самое важное, вектора чувствительны к преобразованиям координат, определенным образом меняя свои компоненты (элементы из ), при координатных преобразованиях оставаясь тем же самым вектором (вот тут-то и сказывается различие между верхними и нижними индексами). В пространства две разных числовых последовательности – это два разных объекта, даже если они суть координаты одного и того же вектора в разных системах координат. Иногда все-таки элементы из называют векторами, основываясь на том, что правило сложения, определенное выше – это в точности правило параллелограмма для сложения векторов. В тех случаях, когда они и не являются векторами по существу, правильнее назвать 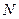- мерные объекты элементами фазового пространства, а представление его в виде линейного векторного пространства ( т.е. состоящего из векторов) рассматривать как модель - представление этого фазового пространства на пространстве векторов.

Частным случаем линейных векторных пространствслужат 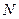- мерные векторные пространства , введенные и рассмотренные в приложении 1.

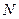векторов линейного векторного пространства независимы (линейно независимы), если из , следует, что все . Если линейное пространство содержит 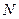линейно независимых векторов, то любые из векторов уже линейно зависимы и, следовательно, существует набор ненулевых чисел , такой что

.

Число 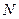называется размерностью линейного векторного пространства.

Элементы из могут быть коэффициентами отрезка ряда Тейлора или отрезка любого другого ряда, например, ряда Фурье или разложения по ортогональным полиномам. Они могут быть и координатами вектора, но этот конкретный смысл важен при решении конкретных практических задач. Понятие Евклидового пространства также требует кое-каких дополнительных свойств. Они будут введены ниже.

Нормы. Линейное пространство становиться линейным нормированным пространством после того, как для каждого его элемента определена норма этого элемента , представляющая собой вещественное число (имеющее смысл «длины» элемента ), удовлетворяющая следующим трем условиям:

1. и тогда и только тогда, когда (определенность);

2. (неравенство треугольника);

3. (однородность).

Типичными примерами конечномерных линейных нормированных пространств (ЛНП), построенных на основе , служат пространства , состоящие из оснащенного нормой:

.

(п.1.1)

Легко увидеть, что условия, наложенные на норму для (1), выполнены.

Для так введенной нормы справедливо неравенство Гельдера:

Если неотрицательные числа 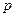и таковы, что , , то

.

Справедливо также, что

Три частных случая являются исключительно важными. Это случаи:

1. ;

2. ;

3.

В последнем случае, пространство с нормой называется Евклидовым. В нем норма равна привычной длине, вычисленной по известному правилу сложения квадратов катетов и последующего извлечения квадратного корня. Учитывая особое значение именно этой нормы, ее будем обозначать без индексных символов: Есть еще одно обобщение нормы . Оно состоит во введении положительных весовых множителей и вычислении нормы в пространстве по правилу:

4. .

Важным понятием является понятие сходимости бесконечной последовательности элементов . Последовательность сходится к элементу (это записывается ), если . Это можно сказать - -предельный элемент для . С точки зрения сходимости, все введенные выше нормы эквивалентны. Точнее говоря, если последовательность сходится к элементу в одной из норм , то она сходится и в любой другой. Однако эта эквивалентность по сходимости совсем не означает эквивалентности по другим свойствам, и, прежде всего свойствам близости элемента к фиксированному множеству .

Выпуклой комбинациейконечного числа элементов называется совокупность всех таких элементов из , которые можно представить в виде и .

Множество , образованное из элементов, все выпуклые комбинации которых вновь принадлежат , называется выпуклым.

Множество , все предельные элементы последовательностей которого вновь принадлежат , называется замкнутым.

Базисными элементами в линейном нормированном пространстве назовем элементы из компоненты, которых для значения индекса 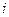равного равны единице, а для остальных значений индекса , эти компоненты равны нулю. Например

……….. .

Тогда каждый элемент можно записать в виде . Это же равенство записывают в форме: . Компоненты независимы, поэтому они не складываются, а сумма понимается как суперпозиция независимых элементов.

Скалярное или внутреннее произведение двух элементов и из : определено равенством . В том случае, если пространства состоят из комплексных чисел:

, где - комплексно сопряженные к числа.

Ясно, что .

Совершенно очевидно, что .

В качестве базисных могут быть выбраны и другие элементы . Условие на базисные элементы состоит в том, что они образуют полную систему в , а это значит, что любой элемент из можно представить в виде . Число элементов базиса в ровно 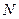. Любой дополнительный базисный элемент, если его ввести может быть выражен в виде линейной комбинации . Наоборот, если взять базисных элементов меньше чем 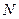, например , то найдутся элементы в непредставимые в этом базисе. И более того, можно сделать так, что эти элементы будут ортогональны всем другим, представимым в виде .

Из неравенства Гельдера следует, что:

и; в частности, при : . Для векторов на плоскости и в пространстве известно, что , где - косинус угла между векторами и соответственно. Тогда величину можно отождествить с «косинусом угла» между произвольными элементами из .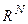

Операторы. Линейным оператором из линейного нормированного пространства (ЛНП) в ЛНП называется отображение , ставящее в соответствие каждому элементу элемент , обладающее свойством линейности:

Для любых двух и чисел (вещественных, либо комплексных, в зависимости от вещественности, либо комплексности и ) :

.

Подадим на «вход оператора элемент Его образом при отображении оказывается

элемент . Это элемент из . Откликом на элемент будет служить и так далее. Откликом на элемент будет . Поскольку любой элемент из представим в виде , то в силу линейности оператора откликом на будет сумма откликов на . Таким образом, действие оператора из в эквивалентно действию на компоненты «вектора» в базисе прямоугольной матрицы:
.

Эта матрица состоит из вещественных чисел, если и вещественные ЛНП, и комплексных, в противном случае. Расчеты проводятся по формуле:

.

Часто пользуются правилом суммирования, согласно которому по дважды повторяющемуся в выражении индексу происходит суммирование по всем его значениям. Тогда .

Алгебра матриц.

Матрицу можно умножить на скаляр, умножив на него все компоненты.

.

Две прямоугольные матрицы одного размера можно сложить, сложив их компоненты:

.

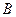Две матрицы можно перемножить. Для этого должны быть согласованы их размерности. Пусть - матрица. - матрица размером . Тогда определено их произведение:

. Результирующая матрица оказывается квадратной размера - размерности или ранга . Важными служат операции комплексного сопряжения матрицы : Комплексно сопряженная матрица к состоит из элементов комплексно сопряженных к элементам матрицы .

Транспонированная матрица получается заменой строк на столбцы. Если - матрица, то - матрица, в которой все строки матрицы заменены ее столюуами. Наконец, сопряженная к матрица . Для вещественных матриц комплексно сопряженная совпадает с исходной – это очевидно. Тогда сопряженная совпадает с транспонированной.

Обратной к матрице называется матрица такая, что . Эта матрица может и не существовать. Но, если она существует, то , где 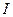- единичная матрица, диагональные элементы которой равны единице, а все остальные – нулю:

.

Следующее свойство сопряженной матрицы является ее строгим определением.

Если - матрица и , то

.

Наибольшее значение имеют квадратные матрицы.

Типы матриц. Матрица называется:

Симметричной, если ;

Ортогональной, если ;

Эрмитовой, если ;

Унитарной, если ;

Легко понять, что унитарные матрицы, примененные к вектору, не меняют его Евклидовой длины . (хотя меняют длину в других определениях нормы). Это следует из равенства .

Нормальной, если .

Невырожденной, если .

Из курса алгебры известно, что для того, чтобы матрица имела обратную, необходимо и достаточно, чтобы ее определитель не был равен нулю. Иными словами, чтобы матрица была невырожденной.

Напомним некоторые свойства определителя:

Определительпроизведения равен произведению определителей:

Поскольку определитель единичной матрицы равен 1: , то отсюда следует, что:

.

.

Определитель матрицы обозначают также символом .

Следующие два утверждения эквивалентны: уравнение имеет ненулевые решения.

Нетрудно понять, что строки вещественной ортогональной матрицы образуют взаимно ортогональные элементы: .

Наконец, матрица называется положительно полуопределенной, если и положительно определенной, если и равенство выполнено только при .

Множество квадратных матриц образует линейное пространство, поскольку на нем определены операции умножения на число и операция умножения, в результате которых возникает вновь квадратная матрица того же ранга.

Норма матриц. Определим норму матрицы правилом[35]:

.

Таим образом, справедливо неравенство:

.

Норма единичной матрицы равна единице: .

Величины и могут быть определены в и соответственно. В этом случае, возникают различные нормы матрицы , в случае индексы в обозначении нормы опускаем.

В том случае, когда , норма векторов рассчитывается по формуле:

, норма рассчитывается по правилу:

.

Действительно:

Норма имеет специальное название – норма Шмидта. . Справедливым является неравенство:

,

которое и определяет эту норму.

Собственные числаи собственные элементы. Для квадратной матрицы порядка N рассмотрим задачу на собственные значения:

.

Числа , для которых решение этого уравнения существует, будем называть собственными числами (значениями), а решения соответствующие этим числам – собственными элементами или векторами, если это последнее название допустимо. Для того чтобы найти все собственные числа, надо решить характеристическое уравнение:

Поскольку определитель квадратной матрицы размерности N - это полином степени N, то корней характеристического уравнения или, что, то же самое, собственных чисел матрицы A ровно N.

Если любая неособенная (невырожденная) матрица того же ранга, то собственные числа матрицы A и совпадают. Это легко понять, поскольку

Следующие свойства собственных чисел практически очевидны:

Если и 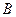две квадратные матрицы, то их произведения, взятые в любом порядке, имеют одни и те же собственные числа.

Если матрица неособенная, то характеристические числа обратной к матрицы равны обратной величине собственных чисел матрицы , т.е. равны .

Любая эрмитова матрица имеет только вещественные собственные числа.

Если эрмитова матрица положительно определена (полуопределена), то ее собственные числа положительны (неотрицательны).

Положительно полуопределенную эрмитову матрицу всегда можно превратить в положительно определенную, исключив из рассмотрения те элементы, для которых . Тогда для остальных элементов форма никогда не будет нулевой, за исключением случая . Это и означает положительную определенность. Напомним, что такие элементы обозначаются и образуют линейное подпространство (в частности, нулевое) в . Всегда можно рассматривать матрицу на ортогональном дополнении к , которое обозначим , которое совпадает с множеством значений самой эрмитовой матрицы . Действительно из следует и элемент оказывается ортогональным любому элементу представимому в виде , т.е. ортогонален подпространству .

Если и наибольшее и наименьшее собственные числа эрмитовой матрицы, то:

Для любой квадратной матрицы матрица эрмитова и положительно полуопределена. Матрицы и имеют одни и те же собственные числа, равные квадрату собственных чисел матрицы .

Унитарная и ортогональная матицы имеют комплексные собственные числа по модулю равные единицы.

Спектральным радиусом матрицы называется максимум модуля собственных чисел. Эти числа могут быть комплексными. Именно поэтому следует брать модуль.

Из сказанного выше следует, что спектральный радиус унитарной матрицы равен единице, а любое неособенное преобразование матрицы оставляет спектральный радиус неизменным (спектральный радиус инвариантен при преобразованиях с помощью неособенной матрицы).

Говорят, что матрицы и 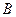унитарно эквивалентны, если существует унитарная матрица 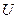и

.

Следующая теорема называется теоремой Шура.

Для любой квадратной матрицы существует унитарная матрица 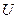такая, что унитарно эквивалентна треугольной матрице , где собственные числа матрицы .

.

Отсюда, в частности, следует, что унитарно эквивалентная матрица к любой квадратной матрице может быть представлена в виде диагональной матрицы 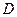, в которой ненулевые члены только те, что стоят на диагонали и равны собственным числам исходной матрицы, и некоторой добавочной , ненулевые члены которой расположены только выше (или только ниже) диагонали. Матрицы и 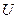определены неоднозначно. Если нормальная матрица, то можно так подобрать 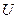, что матрица окажется нулевой - состоящей только из нулей.

Спектральной нормой квадратной матрицы называют положительное значение квадратного корня из наибольшего собственного числа матрицы :

.

Спектральная норма и спектральный радиус совпадают для эрмитовых матриц. В общем же случае спектральный радиус не превосходит спектральной нормы.

Экстремальные свойства собственных чисел.Собственные числа для вполне непрерывных эрмитовых матриц обладают важным экстремальным свойством. Если положительно определенная эрмитова матрица, то ее наибольшее собственное значение, обозначим его , обеспечивает максимум выражению:

при условии, что . Иными словами,

.

Причем, максимум достигается на собственном элементе , соответствующем этому собственному числу. Если этому собственному числу соответствует несколько, например, разных собственных элементов , то максимум - обеспечивается на каждом из них, и само это собственное число называем число кратности . Очевидно, что линейная комбинация собственных элементов (векторов), соответствующих одному собственному числу, есть снова собственный элемент, соответствующий этому собственному числу. Действительно,

Сумма кратностей всех собственных чисел равна размерности эрмитовой положительно определенной матрицы.

Далее второе собственное число обладает теми же экстремальными свойствами, но уже на подпространстве в , ортогональном ко всем элементам :

Пусть это число имеет кратность и его собственные элементы . Процесс можно продолжить и собственное число оказывается решением экстремальной задачи:

Здесь подпространство в , ортогональном ко всем элементам . . ортогонально подпространству в натянутому на . . Процесс этот можно продолжить, расположив собственные числа в порядке убывания, суммарная кратность которых равна 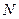. Займемся теперь собственными элементами.

Для эрмитовых матриц собственные элементы, принадлежащие различным собственным числам ортогональны.

Действительно, пусть и .

Тогда . Но при , следует что

Аналогичное положение дел имеет место для ортогональных и унитарных операторов. (Их собственные числа по модулю равны единице). Доказывается это следующим образом. Пусть и .

Тогда .

Поскольку