Условия устойчивости линейных САР
Общее условие устойчивости линейных систем
Для устойчивости линейной системы необходимо и достаточно, чтобы вещественная часть всех собственных значений матрицы A (корней характеристического уравнения) была отрицательной, т. е.
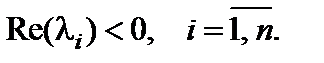(6.4)
Покажем справедливость этого утверждения, для чего запишем характеристическое уравнение системы
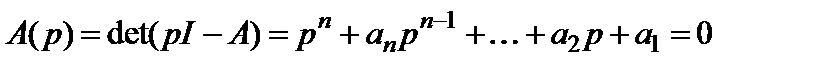(6.5)
и найдем его корни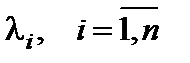 
. Используя модальное представление, определим полный процесс в системе, который представляет собой сумму экспонент
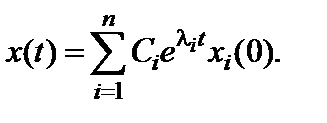(6.6)
Как видим, качественный характер переходных процессов полностью определяется значениями корней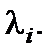 
В случае, когда все они вещественные и отрицательные, каждая компонента выражения (6.6) при выполнении условия (6.4) носит затухающий характер (рис.6.5). Следовательно, и их сумма также будет иметь затухающий характер, т. е. будет с течением времени стремиться к нулю.
Если корни характеристического уравнения (6.5) комплексно-сопряженные с отрицательной вещественной частью, то каждая пара их дает колебательную составляющую процесса, которая мажорируется затухающей экспонентой (рис. 6.6).
1– расходящийся; 2 – затухающий
Рис. 6.5. Иллюстрация процесса в системе с
Вещественным корнем
Следовательно, и в этом случае процесс, определяемый соотношением (6.6), будет иметь затухающий характер.
Таким образом, мы показали достаточность условия устойчивости (6.4).
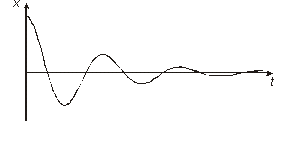
Рис.6.6. Колебательная составляющая процесса
в случае отрицательной вещественной части пары
комплексно-сопряженных корней
Покажем теперь необходимость этого условия. Предположим, что хотя бы один из корней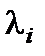 
имеет положительную вещественную часть. Соответствующая ему составляющая решения будет с течением времени возрастать и в пределе стремиться к бесконечности (рис. 6.7). Следовательно, полный процесс, который определяется выражением (6.6), будет иметь расходящийся характер, а система никогда не сможет стать устойчивой.
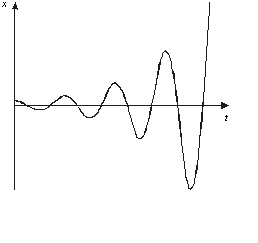
Рис. 6.7. Процесс в системе с положительной вещественной
частью пары
комплексно-сопряженных корней
Изобразим корневой портрет системы (рис. 6.8) и получим графическую интерпретацию условия (6.4): для устойчивости линейной системы необходимо и достаточно, чтобы все корни характеристического уравнения располагались в левой полуплоскости плоскости корней.
Рис. 6.9. процесс в системе с «мнимыми» корнями
Если хотя бы один корень находится в правой полуплоскости плоскости корней, то система будет неустойчива. Мнимая ось представляет собой границу устойчивостисистемы: при расположении комплексно-сопряженных корней на этой оси система находится на границе устойчивости (при условии, что все остальные корни имеют отрицательную вещественную часть). При этом процессы имеют вид незатухающих колебаний (рис. 6.9).