Задачи линейного программирования
Графический метод решения задачи линейного программирования (ЛП) целесообразно использовать для решения задач с двумя переменными и для решения задач с несколькими переменными при условии, что в канонической записи системы ограничений содержится не более двух свободных переменных.
Запишем задачу ЛП с двумя переменными в канонической форме:
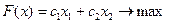 (2.1)
(2.1)
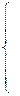
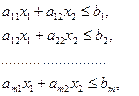 (2.2)
(2.2)
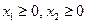 .
.
Для того, что бы изобразить графически множество неотрицательных решений системы неравенств, строятся прямые 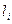
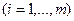 :
: 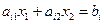 .
.
Каждая построенная прямая 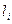 , делит всю плоскость на две полуплоскости. При этом, координаты точек только одной полуплоскости удовлетворяют соответствующему неравенству
, делит всю плоскость на две полуплоскости. При этом, координаты точек только одной полуплоскости удовлетворяют соответствующему неравенству  . Для того, чтобы найти какую полуплоскость определяет неравенство
. Для того, чтобы найти какую полуплоскость определяет неравенство  , можно взять любую точку, не принадлежащую прямой
, можно взять любую точку, не принадлежащую прямой 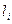 и подставить ее координаты в неравенство
и подставить ее координаты в неравенство  . Если неравенство выполняется, то искомая полуплоскость та, которая содержит рассматриваемую точку; если неравенство не выполняется, то искомая полуплоскость та, которая не содержит рассматриваемую точку.
. Если неравенство выполняется, то искомая полуплоскость та, которая содержит рассматриваемую точку; если неравенство не выполняется, то искомая полуплоскость та, которая не содержит рассматриваемую точку.
Известно, что множеством решений системы ограничений (2.2) является либо выпуклый многоугольник, либо выпуклая многоугольная область, при условии, что система (2.2) совместна. Множество неотрицательных решений системы (2.2), называют множеством допустимых решений.
Предположим, что множество допустимых решений системы (2.2) не пусто. Предположим также, что целевая функция 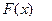 ограничена на множестве допустимых решений системы (2.2) в задаче на максимум сверху (в задаче на минимум - снизу). В этом случае задача ЛП на максимум (минимум) имеет, по крайней мере, одно решение.
ограничена на множестве допустимых решений системы (2.2) в задаче на максимум сверху (в задаче на минимум - снизу). В этом случае задача ЛП на максимум (минимум) имеет, по крайней мере, одно решение.
Для нахождения оптимального решения задачи ЛП графически, построим нулевую линию уровня 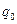 , уравнение которой
, уравнение которой 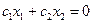 (
( 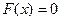 ). Нулевая линия уровня
). Нулевая линия уровня 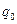 - это прямая, проходящая через начало координат перпендикулярно вектору нормали
- это прямая, проходящая через начало координат перпендикулярно вектору нормали 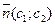 . Другие линии уровня
. Другие линии уровня 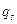 , заданные уравнениями
, заданные уравнениями 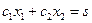
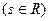 построим параллельно
построим параллельно 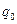 . Вдоль каждой линии
. Вдоль каждой линии 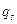 значение целевой функции
значение целевой функции 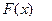 постоянно и равно
постоянно и равно 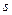 .
.
Вектор 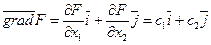 указывает направление наискорейшего возрастания целевой функции
указывает направление наискорейшего возрастания целевой функции 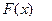 . Для линейной целевой функции вектор
. Для линейной целевой функции вектор 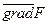 расположен перпендикулярно линиям уровня. Если переходить от одной линии уровня к другой в направлении вектора-градиента, то значение целевой функции
расположен перпендикулярно линиям уровня. Если переходить от одной линии уровня к другой в направлении вектора-градиента, то значение целевой функции 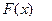 будет возрастать и достигнет максимума в последней точке
будет возрастать и достигнет максимума в последней точке 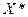 соприкосновения линии уровня
соприкосновения линии уровня 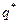 с областью допустимых решений системы неравенств (2.2).
с областью допустимых решений системы неравенств (2.2).
Заметим, что задача ЛП может иметь и бесчисленное множество решений. Это возможно, когда целевая функция достигает наибольшего значения в двух соседних вершинах области допустимых решений системы (2.2), а значит и вдоль всего отрезка соединяющего эти вершины. В этом случае говорят, что задача ЛП имеет альтернативное решение. Например, пусть целевая функция в задаче ЛП достигает максимального значения в области допустимых решений на всем отрезке 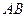 :
: 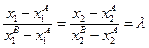
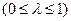 , где
, где 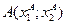 и
и 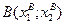 , в этом случае оптимальное решениезадачи можно записать в виде:
, в этом случае оптимальное решениезадачи можно записать в виде: 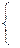
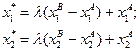
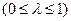 .
.
Задача №2.1.
Изобразить графически множество неотрицательных решений системы неравенств:
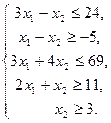 .
. 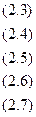
Решение.
В системе координат 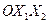 построим граничные прямые
построим граничные прямые 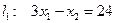 ;
; 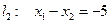 ;
; 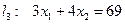 ;
; 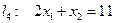 ;
; 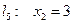 .
.

рис. 2.1
Каждая построенная прямая 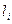
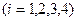 , делит всю плоскость на две полуплоскости. Определим полуплоскости, координаты точек, которых удовлетворяют соответствующему неравенству. Так как ни одна из прямых не проходит через начало координат, то для определения нужной полуплоскости возьмем точку
, делит всю плоскость на две полуплоскости. Определим полуплоскости, координаты точек, которых удовлетворяют соответствующему неравенству. Так как ни одна из прямых не проходит через начало координат, то для определения нужной полуплоскости возьмем точку 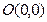 .
.
Например, координаты точки 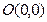 удовлетворяют неравенству (2.3), т.к.
удовлетворяют неравенству (2.3), т.к. 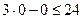 . Следовательно, искомая полуплоскость та, которая содержит точку
. Следовательно, искомая полуплоскость та, которая содержит точку 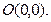 Координаты точки
Координаты точки 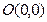 не удовлетворяют неравенству (2.6), т.к.
не удовлетворяют неравенству (2.6), т.к. 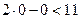 . Следовательно, искомая полуплоскость та, которая не содержит точку
. Следовательно, искомая полуплоскость та, которая не содержит точку 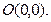
Отметив для каждого неравенства область решений, найдем пересечение всех отмеченных областей, получим выпуклый пятиугольник 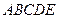 . Область
. Область 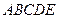 лежит в первой четверти, следовательно, найдена область неотрицательных решений системы неравенств (2.3) –(2.7).
лежит в первой четверти, следовательно, найдена область неотрицательных решений системы неравенств (2.3) –(2.7).
Задача № 2.2.
На множестве неотрицательных решений системы неравенств
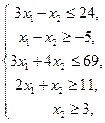 (2.8)
(2.8)
найти решение задачи линейного программирования:
1) 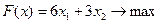 ;
;
2) 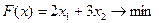 ;
;
3) 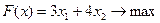 .
.
Решение.
Областью неотрицательных решений системы неравенств (2.8) является выпуклый пятиугольник 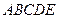 (см. решение предыдущей задачи).
(см. решение предыдущей задачи).
1) Построим нулевую линию уровня 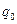 :
: 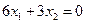 (
( 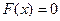 ). Прямая
). Прямая 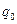 проходит через начало координат перпендикулярно вектору нормали
проходит через начало координат перпендикулярно вектору нормали 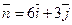 .
.
Построим вектор-градиент 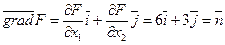 .
.
В направлении вектора 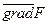 значение целевой функции
значение целевой функции 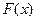 будет расти и достигнет максимума в последней точке соприкосновения линии уровня
будет расти и достигнет максимума в последней точке соприкосновения линии уровня 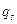 с областью допустимых решений, в точке
с областью допустимых решений, в точке 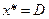 (рис. 2.2). Линию уровня, проходящую через
(рис. 2.2). Линию уровня, проходящую через 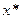 , обозначим
, обозначим 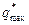 .
.
Определим координаты точки 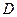 :
: 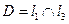 . Решим систему
. Решим систему 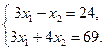
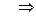
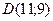 . Отсюда оптимальное решение
. Отсюда оптимальное решение 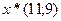 , при этом
, при этом 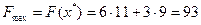 .
.
2) Построим нулевую линию уровня 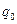 :
: 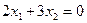 (
( 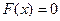 ). Прямая
). Прямая 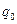 проходит через начало координат перпендикулярно вектору нормали
проходит через начало координат перпендикулярно вектору нормали 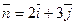 .
.
Направлением наискорейшего убывания функции 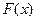 , будет направление обратное вектору
, будет направление обратное вектору 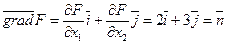 . Поэтому оптимальным решением задачи будет первая точка соприкосновения линии уровня
. Поэтому оптимальным решением задачи будет первая точка соприкосновения линии уровня 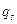 с областью допустимых решений, т.е. точка
с областью допустимых решений, т.е. точка 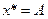 (рис. 2.3). Координаты точки
(рис. 2.3). Координаты точки  найдем из условия
найдем из условия 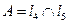 . Решим систему
. Решим систему 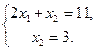
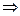
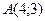 . Следовательно, оптимальное решение
. Следовательно, оптимальное решение 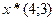 , при этом
, при этом 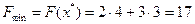
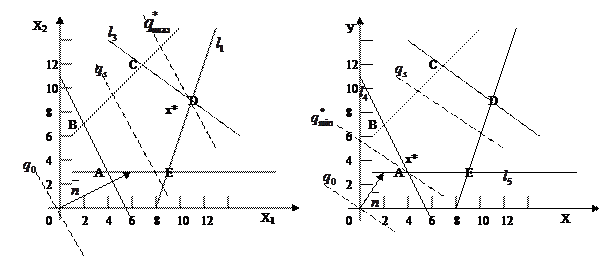
Рис. 2.2 рис. 2.3
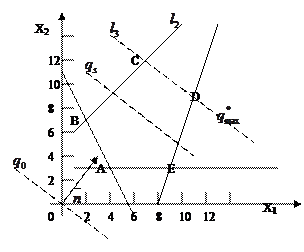
Рис. 2.4
3) Построим нулевую линию уровня 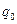 :
: 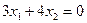 (
( 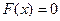 ). Прямая
). Прямая 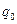 проходит через начало координат перпендикулярно вектору нормали
проходит через начало координат перпендикулярно вектору нормали 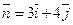 .
.
Направление наискорейшего возрастания функции 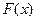 , будет определять вектор
, будет определять вектор 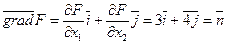 . Передвигая линию уровня
. Передвигая линию уровня 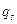 , от нулевой
, от нулевой 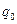 в направление вектора
в направление вектора 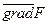 заметим, что решением задачи будет весь отрезок
заметим, что решением задачи будет весь отрезок 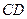 (рис. 2.4), так как линии уровня
(рис. 2.4), так как линии уровня 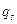 параллельны отрезку
параллельны отрезку 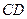 . Следовательно, решением задачи будет множество точек
. Следовательно, решением задачи будет множество точек 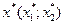 , где
, где 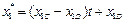 ;
; 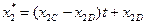
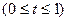 .
.
Координаты точки 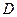 известны:
известны: 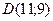 . Определим координаты точки
. Определим координаты точки 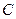 :
: 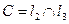 . Решим систему
. Решим систему 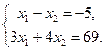
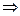
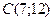 .
.
Отсюда 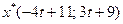
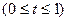 . Для того, чтобы найти
. Для того, чтобы найти 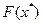 , достаточно вычислить значение целевой функции в одной из точек
, достаточно вычислить значение целевой функции в одной из точек 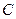 или
или 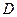 , получим одно и то же значение:
, получим одно и то же значение: 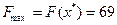 .
.
Задача № 2.3.
Задачу ЛП решить графически:
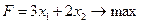
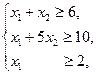 (2.9)
(2.9)
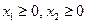 .
.
Решение.
В системе координат 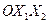 построим граничные прямые
построим граничные прямые 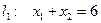 ;
; 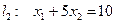 ;
; 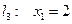 . Решением системы неравенств будет выпуклая не ограниченнная многоугольная область. На рис. 2.5 область неотрицательных решений системы (2.9) отмечена штриховкой.
. Решением системы неравенств будет выпуклая не ограниченнная многоугольная область. На рис. 2.5 область неотрицательных решений системы (2.9) отмечена штриховкой.
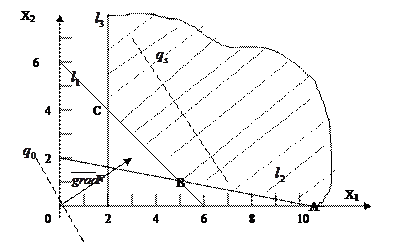
Рис.2.5
Линии уровня 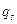 в направлении вектора
в направлении вектора 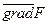 могут удаляться в бесконечность, оставаясь в области допустимых решений, то есть целевая функция в данной задаче неограниченна и задача не имеет оптимального решения.
могут удаляться в бесконечность, оставаясь в области допустимых решений, то есть целевая функция в данной задаче неограниченна и задача не имеет оптимального решения.
Задача № 2.4.
Найти область неотрицательных решений системы неравенств
а) 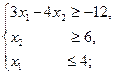 (2.10) в)
(2.10) в) 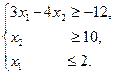 . (2.11)
. (2.11)
Решение.
а) Решением системы неравенств (2.10) является точка А(4;6) (рис. 2.6).
в) Система неравенств (2.11) не имеет решения (рис. 2.7).
 | |||
 | |||
Рис.2.6 рис. 2.7
Задача № 2.5.
Решить задачу №1.1 графически.
Решение.
В задаче №1.1 построена модель задачи ЛП:
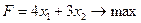
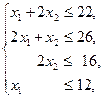 (2.12)
(2.12)
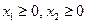 .
.
Необходимо спланировать объемы производства 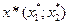 продукции вида
продукции вида 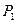 и вида
и вида 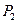 таким образом, чтобы максимизировать прибыль
таким образом, чтобы максимизировать прибыль 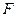 , не выходя за рамки производственных возможностей, заданных системой (2.12).
, не выходя за рамки производственных возможностей, заданных системой (2.12).
1) Построим систему координат 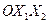 . По оси
. По оси 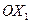 будем откладывать объемы производства продукции
будем откладывать объемы производства продукции 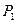 , по оси
, по оси 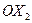 - объемы производства продукции
- объемы производства продукции 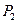 .
.
В системе координат 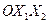 построим граничные прямые:
построим граничные прямые: 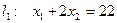 ;
; 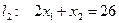 ;
; 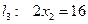 ;
; 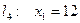 . Областью допустимых решений системы ограничений (2.12) будет шестиугольник
. Областью допустимых решений системы ограничений (2.12) будет шестиугольник 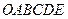 . Координаты всех точек, лежащих внутри и на границе шестиугольника
. Координаты всех точек, лежащих внутри и на границе шестиугольника 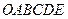 удовлетворяют системе неравенств (2.12). Шестиугольник
удовлетворяют системе неравенств (2.12). Шестиугольник 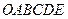 - это область производственных возможностей. Любая точка шестиугольника
- это область производственных возможностей. Любая точка шестиугольника 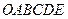 , соответствует объемам производства продукции
, соответствует объемам производства продукции 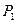 и
и 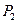 , для которых имеющихся в наличии ресурсов будет достаточно. Наша задача из всех точек, принадлежащих множеству производственных возможностей выбрать ту, которая соответствует наибольшему значению прибыли, получаемой при реализации всей произведенной продукции.
, для которых имеющихся в наличии ресурсов будет достаточно. Наша задача из всех точек, принадлежащих множеству производственных возможностей выбрать ту, которая соответствует наибольшему значению прибыли, получаемой при реализации всей произведенной продукции.
2) Построим вектор-градиент 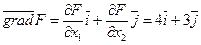 . Через начало координат перпендикулярно вектору
. Через начало координат перпендикулярно вектору 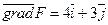 проведем нулевую линию уровня
проведем нулевую линию уровня 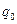 :
: 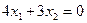 (
( 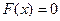 ). Прямая
). Прямая 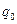 с областью производственных возможностей имеет только одну общую точку О(0;0), которая соответствует нулевым объемам производства.
с областью производственных возможностей имеет только одну общую точку О(0;0), которая соответствует нулевым объемам производства.
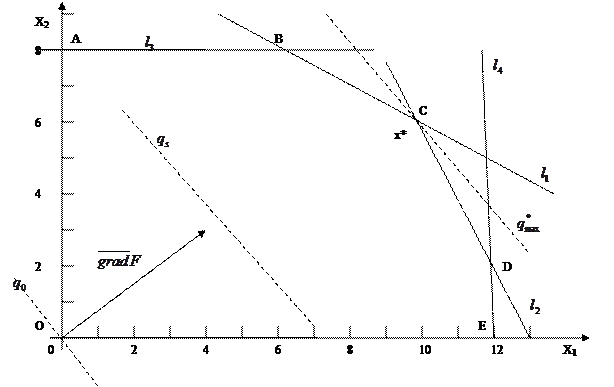
рис. 2.8
В направлении вектора 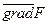 значение целевой функции
значение целевой функции 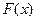 будет расти
будет расти
Строя линии уровня 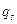 в направлении
в направлении 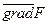 , будем получать линии равных производственных возможностей, т.е. при разных объемах производства значение прибыли вдоль всей линии
, будем получать линии равных производственных возможностей, т.е. при разных объемах производства значение прибыли вдоль всей линии 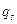 будет постоянно. Чем северо-восточней расположена линия уровня, тем большему значению прибыли она соответствует.
будет постоянно. Чем северо-восточней расположена линия уровня, тем большему значению прибыли она соответствует.
Целевая функция 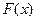 достигнет максимума в последней точке соприкосновения линии уровня
достигнет максимума в последней точке соприкосновения линии уровня 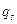 с областью допустимых решений, в точке
с областью допустимых решений, в точке 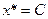 (рис. 2.8). Линию уровня, проходящую через
(рис. 2.8). Линию уровня, проходящую через 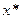 , обозначим
, обозначим 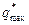 .
.
3) Определим координаты точки 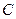 :
: 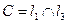 . Решим систему
. Решим систему 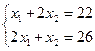
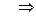
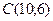 .
.
Отсюда оптимальное решение 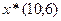 , при этом
, при этом 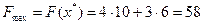 .
.
Ответ: Оптимальные объемы производства продукции 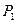 - 10 единиц; продукции
- 10 единиц; продукции 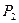 - 6 единиц. Прибыль, получаемая при реализации всей изготовленной продукции, составит 58 д.е.
- 6 единиц. Прибыль, получаемая при реализации всей изготовленной продукции, составит 58 д.е.
Задачи для самостоятельного решения:
Задача № 2.6.
На множестве неотрицательных решений системы неравенств
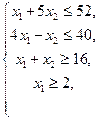 ,
,
найти решение задачи линейного программирования:
1) 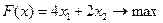 ;
;
2) 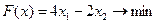 ;
;
3) 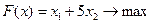 .
.
Задача № 2.7.
Задачу ЛП решить графически:
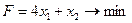
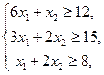
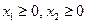 .
.
Задача № 2.8.
Задачу ЛП решить графически:
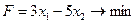
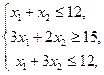
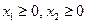 .
.
Задача № 2.9.
Задачу ЛП решить графически:
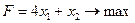
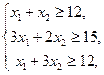
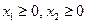 .
.
Задача № 2.10.
Решить графически задачу № 1.2.
Задача № 2.11.
Решить графически задачу № 1.11.
Задача № 2.12.
Решить графически задачу № 1.19.
Симплексный метод
Решить задачу ЛП можно методом перебора конечного числа опорных решений и выбрать среди них то, при котором функция цели достигает своего наибольшего (наименьшего) значения.
Но на практике число опорных решений может быть достаточно велико. Существует алгоритм, позволяющий на каждом шаге получать решения, по крайней-мере не хуже, чем на предыдущем шаге. Такой перебор позволяет сократить число шагов. Данный метод называется симплексным методом.
Геометрический смысл симплексного метода состоит в последовательном переходе от одной вершины многогранника допустимых решений к соседней, в которой целевая функция принимает значение “по крайней мере” не худшее, до тех пор, пока не будет найдено оптимальное.
Симплексный метод предусматривает три основных элемента:
1) способ определения какого-либо первоначального базисного решения задачи;
2) правило перехода к лучшему (по крайней мере, к не худшему) решению;
3) критерий проверки оптимальности найденного решения.
Если ранг системы уравнений равен m , то в качестве базисных переменных на первом шаге рекомендуется выбрать (если это возможно) такие m переменных, каждая из которых, входит только в одно из m уравнений системы ограничений, и нет таких уравнений, в которые бы не входила бы не одна из этих переменных.
Критерий оптимальности решения при отыскании максимума (минимума) целевой функции в задаче ЛП: если в выражении целевой функции через свободные переменные отсутствуют положительные (отрицательные) коэффициенты при свободных переменных, то решение оптимально.
