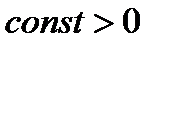Сложность универсального многополюсника
Универсальный многополюсник.
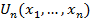
Входами этого многополюсника являются переменные  , а выходами
, а выходами  , где
, где 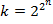 , и эти выходы соответствуют всевозможным функциям от n переменных.
, и эти выходы соответствуют всевозможным функциям от n переменных.
Утверждение. Сложность многополюсника
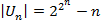
Докажем нижнюю оценку 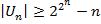 . Действительно, многополюсник имеет
. Действительно, многополюсник имеет 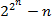 выходов, которым соответствуют различные двоичные функции, поэтому на реализацию каждого выхода требуется по крайней мере
выходов, которым соответствуют различные двоичные функции, поэтому на реализацию каждого выхода требуется по крайней мере 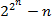 различных элементов.
различных элементов.
Докажем верхнюю оценку 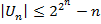 . Рассмотрим произвольную схему, которая реализует все нетождественные функции не более чем от
. Рассмотрим произвольную схему, которая реализует все нетождественные функции не более чем от 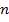 переменных. Для этого, например, можно использовать представление функции в виде СДНФ. Тогда каждой вершине схемы будет соответствовать нетождественная функция. Для каждой нетождественной функции рассмотрим вершины, в которых реализуется данная функция. Среди этих вершин рассмотрим ту, глубина которой наименьшая (ту, которая расположена наиболее близко к входам схемы). Тогда удалим оставшиеся вершины соответствующие данной функции и присоединим выходы рассмотренной вершины ко выходам удаленных вершин (т.к. выходы удаленных вершин могут быть использованы для реализации каких либо других функций). Данную операцию выполним для всех нетождественных функций не более чем от
переменных. Для этого, например, можно использовать представление функции в виде СДНФ. Тогда каждой вершине схемы будет соответствовать нетождественная функция. Для каждой нетождественной функции рассмотрим вершины, в которых реализуется данная функция. Среди этих вершин рассмотрим ту, глубина которой наименьшая (ту, которая расположена наиболее близко к входам схемы). Тогда удалим оставшиеся вершины соответствующие данной функции и присоединим выходы рассмотренной вершины ко выходам удаленных вершин (т.к. выходы удаленных вершин могут быть использованы для реализации каких либо других функций). Данную операцию выполним для всех нетождественных функций не более чем от 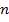 переменных. В полученной схеме количество вершин будет соответствовать количеству нетождественных функций не более чем от
переменных. В полученной схеме количество вершин будет соответствовать количеству нетождественных функций не более чем от 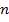 переменных, т.е.
переменных, т.е. 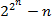 .
.
Что и требовалось доказать.
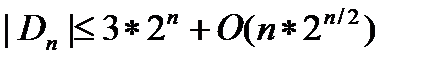
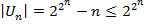
Основная задача – оценить число элементов, необходимых и достаточных для реализации любых двоичных функций не более чем от 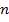 переменных. Покажем, что
переменных. Покажем, что
6.4 Оценка сложности функций n переменных 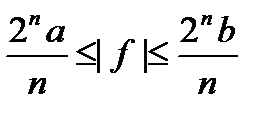 .
.
Утвердение
Сложность любой двочной функции не более чем n перменных лежит в пределах:

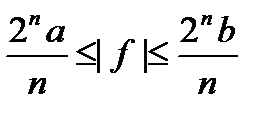
при некоторых положительных константах 
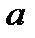 и
и 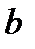 .
.
Доказательство:
Покажем справедливость верхней оценки. Рассмотрим любую двоичную функцию 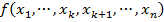 и разложим данную функцию
и разложим данную функцию 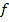 по первым
по первым 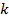 переменным. Справедлива формула
переменным. Справедлива формула 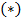 :
:
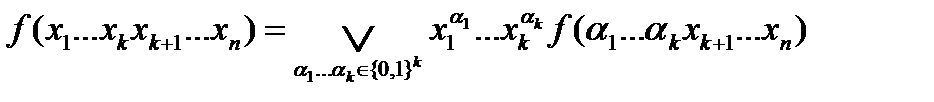 (*)
(*)
.
По данной формуле построим схему, которая будет вычислять данную 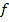 . Реализуем схему вычисления следующим образом:
. Реализуем схему вычисления следующим образом:
 |
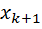 |
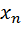 |
 |
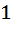 |
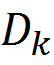 |
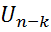 |
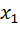 |
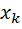 |
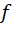 |
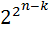 |
 |
Рассмотрим дешифрование порядка 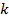 , где
, где 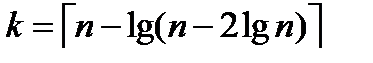 . Скобками
. Скобками 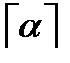 обозначают минимальное натуральное число превосходящее действительное число
обозначают минимальное натуральное число превосходящее действительное число 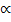 .
.
( логарифм по основанию 2). Очевидны оценки:
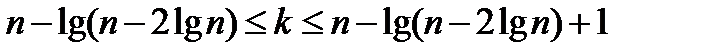
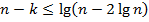
Схема нарисована согласно формуле 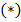 , т.е. на остаточные входы дешифратора подаются соответствующие функции от
, т.е. на остаточные входы дешифратора подаются соответствующие функции от 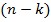 переменных, которые получаются универсальным многополюсником.
переменных, которые получаются универсальным многополюсником.
Т.о. сложность построенной схемы:
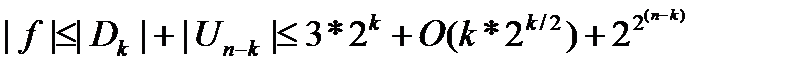
Покажем, что каждое слагаемое есть 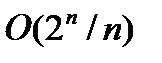
1) 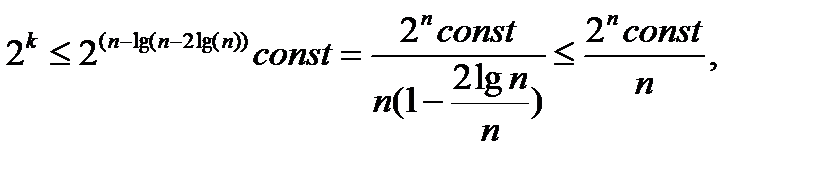
т.к. 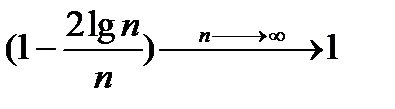 , поэтому ограничена;
, поэтому ограничена;
2) 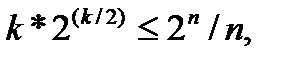 т.к.
т.к. 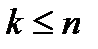 ,
, 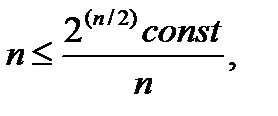
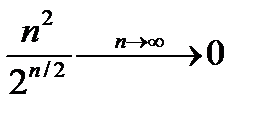 , поэтому ограничена;
, поэтому ограничена;
3) 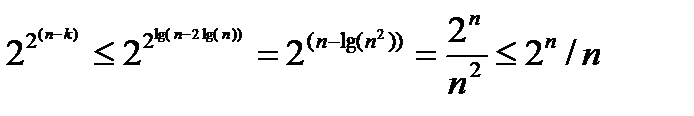 .
.
Требуемое доказано. Оценим сложность функции снизу, применяя мощностной метод.
Пусть число функциональных элементов 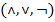 в схеме
в схеме 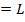 . Обозначим символом
. Обозначим символом 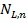 число схем с
число схем с 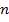 входами, число элементов в которых
входами, число элементов в которых 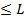 . Покажем, что число таких схем удовлетворяет оценке:
. Покажем, что число таких схем удовлетворяет оценке: 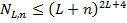 .
.
Действительно, элементы схемы можно разбить на 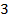 группы с числом конъюнкций
группы с числом конъюнкций 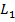 , дизъюнкций
, дизъюнкций 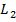 и отрицаний
и отрицаний 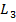 не более чем
не более чем 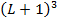 способами (единица в формуле появляется в силу того, что некоторые группы могут быть пустыми). Теперь перечислим всевозможные соединения элементов. Каждый элемент в схеме имеет не более 2-х входов. Каждый вход можно соединить не более чем с
способами (единица в формуле появляется в силу того, что некоторые группы могут быть пустыми). Теперь перечислим всевозможные соединения элементов. Каждый элемент в схеме имеет не более 2-х входов. Каждый вход можно соединить не более чем с 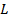 выходами других элементов, либо с
выходами других элементов, либо с 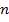 входами
входами  схемы.
схемы.
Поэтому общее число соединений одного элемента не больше 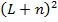 , а т.к. элементов не превосходит
, а т.к. элементов не превосходит 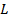 , то общее число соединений элементов не больше чем
, то общее число соединений элементов не больше чем 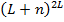 .
.
Осталось назначить общий выход схемы, это можно сделать 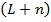 способами (в схеме
способами (в схеме 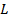 элементов и
элементов и 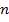 выходов). Таким образом, общее число схем не превосходит
выходов). Таким образом, общее число схем не превосходит 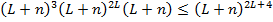 , т.к. число переменных в схеме не менее 1.
, т.к. число переменных в схеме не менее 1.
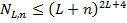
Что и требовалось доказать.
В качестве 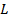 возьмем сложность
возьмем сложность 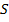 , т.е. минимальное число элементов для реализации всех функций от
, т.е. минимальное число элементов для реализации всех функций от 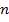 переменных выполняется:
переменных выполняется: 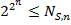 . Т.е. число различным схем сложности
. Т.е. число различным схем сложности 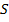 не менее общего числа функций от
не менее общего числа функций от 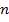 переменных. В противном случае некоторая функция от
переменных. В противном случае некоторая функция от 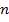 переменных не могла быть реализована схемой сложности
переменных не могла быть реализована схемой сложности 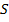 .
.
Используя оценку 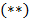 получаем
получаем  . Прологарифмируем данное неравенство:
. Прологарифмируем данное неравенство: 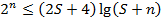 . Используя полученную ранее верхнюю оценку сложности для функции Шенона легко показать необходимую оценку.
. Используя полученную ранее верхнюю оценку сложности для функции Шенона легко показать необходимую оценку.
Справедливы следующие элементарные арифметические выкладки:
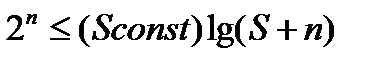
по ранее полученной оценке Шеноновская сложность двоичных функций от 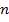 переменных в асимптотике:
переменных в асимптотике:
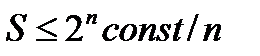
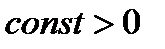 , поэтому
, поэтому 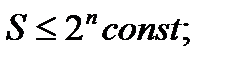 ,
, 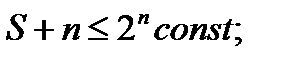 поэтому
поэтому
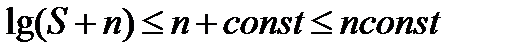 ,
,
тогда 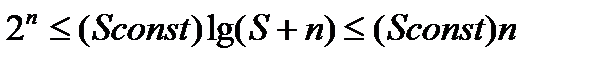 ;
; 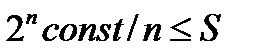
при некоторой положительной константе