Курс, осенний семестр, 5 факультет (68 ч)
ТЕОРЕТИЧЕСКИЕ ВОПРОСУ К КОЛЛОКВИУМУ №1
ПО ВЫСШЕЙ МАТЕМАТИКЕ
(5 фак. 68 часов)
(Второй курс, осенний семестр (третий семестр))
ЧИСЛОВЫЕ РЯДЫ
1. Понятие числового ряда, его частичной суммы, сходимости и расходимости.
2. Необходимый признак сходимости (достаточный признак расходимости) числового ряда.
3. Ряд остаточных членов, свойства. Приближенное вычисление суммы сходящегося ряда.
4. Критерий Коши сходимости числового ряда и его применение для доказательства расходимости гармонического ряда.
5. Простейшие действия над рядами. Основные свойства сходящихся рядов.
6. Знакопостоянные числовые ряды. Критерий сходимости для рядов с неотрицательными членами относительно его частичных сумм.
7. Признак Маклорена-Коши (интегральный признак Коши) сходимости числового ряда с неотрицательными членами. Ряд Дирихле.
8. Признаки сравнения для числовых рядов с неотрицательными членами (первый и второй, соответственно в непредельной и предельной формах).
9. Признак Даламбера в предельной и непредельной формах.
10. Радикальный признак Коши в предельной и непредельной формах.
11. Знакопеременные ряды. Понятие абсолютной и условной сходимости.
12. Теорема Эйлера.
13. Знакочередующиеся ряды. Признак Лейбница и следствие из него.
ФУНКЦИОНАЛЬНЫЕ РЯДЫ
I. Степенные ряды.
14. Определение функционального ряда, понятие частичной суммы, сходимости в точке, области сходимости. Понятие поточечной и равномерной сходимости. Критерий Вейерштрасса (мажорантный признак). Свойства равномерно сходящихся рядов. Нахождение области сходимости функциональных рядов.
15. Степенные ряды. Основная теорема степенных рядов "Теорема Абеля".
15. Понятие радиуса сходимости. Алгоритм исследования степенного ряда на сходимость.
16. Свойства степенных рядов. Теорема единственности разложения функции в степенной ряд.
17. Ряд Тейлора. Необходимые и достаточные условия разложимости функции в ряд Тейлора (Теорема 1: необходимое и достаточное условие через остаточный член формулы Тейлора и Теорема 2: достаточное условие через ограниченность производных).
18. Алгоритм разложения функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора (Маклорена).
19. Табличные разложения основных элементарных функций.
20. Приложения степенных рядов: вычисление приближенного значения функций 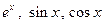 в точке
в точке 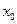 , нахождение приближенных значений корней.
, нахождение приближенных значений корней.
21. Приближенной вычисление значений логарифмов, приложение степенных рядов для вычисления пределов и интегралов, решения линейных дифференциальных уравнений высших порядков с переменными коэффициентами.
ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ К КОЛЛОКВИУМУ №2
ПО ВЫСШЕЙ МАТЕМАТИКЕ
КУРС, ОСЕННИЙ СЕМЕСТР, 5 ФАКУЛЬТЕТ (68 ч)
