Несимметричные вынужденные колебания

Несимметричные колебания СП с нелинейными элементами

Смещение может возникать из-за постоянного внешнего возмущения, несимметрии характеристики нелинейного звена и т. п.

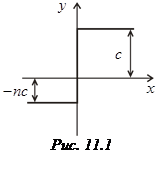
Рассмотрим простейший случай – несимметричную характеристику вида (рис. 11.1):

.

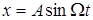Из-за несимметрии к гармонической (переменной) составляющей 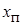добавляется постоянная составляющая :

.

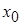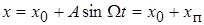Тогда:

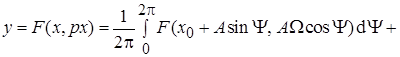
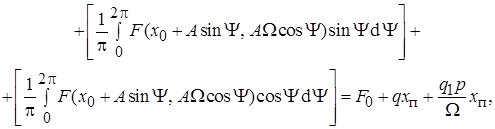
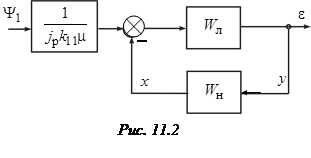где 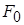– смещение выходной величины. Таким образом необходимо отыс-кать три неизвестных: 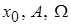– параметры автоколебаний со смещенным центром. При постоянном внешнем воздействии выражения аналогичны. Далее будет рассмотрен именно такой случай.

Обратимся к платформе с нелинейным симметричным ДУε. Смещение центра колебаний происходит за счет постоянного возмущающего момента 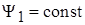. Будем считать, что 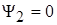(момент по оси прецессии), т. е. он слабо влияет на величину угла ε. Структурная схема при 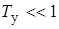примет вид, показанный на рис. 11.2.

Передаточная функция линейного звена:

,

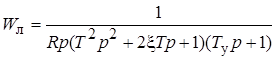где .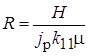

Найдем ,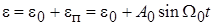

где 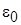– постоянная составляющая 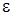; 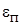– переменная составляющая.

Уравнение системы получается из структурной схемы:

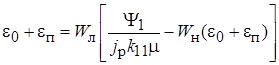, (11.3)

где 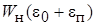стремится к значению .

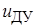Напомним, что на выходе нелинейного элемента после линеаризации:

,

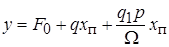т. е. 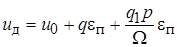. Подставим 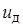в (11.3), получим линеаризованное уравнение системы:

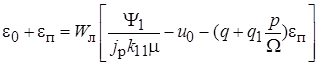. (11.4)

Учитывая, что 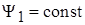или медленно меняющаяся величина, уравнение (11.4) можно представить в виде двух уравнений:

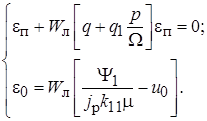
Первое уравнение описывает периодическое движение системы относительно центра 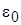, второе – положение центра колебаний в зависимости от воздействия 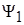. Подставляя в первое уравнение 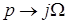, получим из него следующие уравнения:

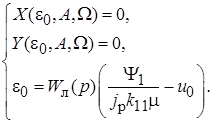
Из данной системы можно получить все необходимые параметры. Поскольку 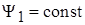, то последнее дифференциальное уравнение следует рассматривать как 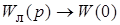, т. е. учитывать только свободный член операторного многочлена звена :

.

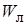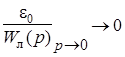Тогда окончательно получим систему:

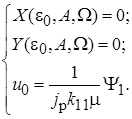
Первые два уравнения будут отличаться только видом 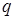и :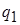

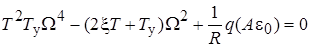; (11.5)

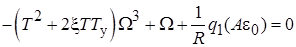. (11.6)

При симметричной нагрузке и при однозначной характеристике:

,

;

.

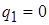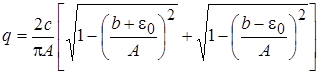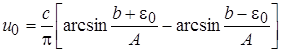Автоколебания возможны только при 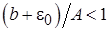, т. е. 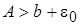. Из (11.6) при 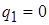находим частоту автоколебаний:

.

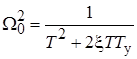Параметры 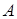и 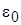найти таким образом сложно, сделать это возможно графически или с помощью вычислительных устройств. Для более простого случая – релейной характеристики будут следующие уравнения при :

; .

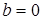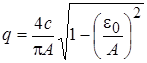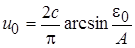Подставляя в (11.5), получим:

,

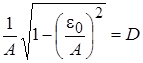где 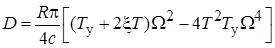. Откуда амплитуда автоколебаний:

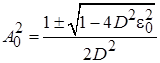; (11.7)

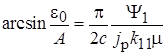или 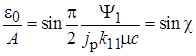. (11.8)

Подставив (11.8) в (11.7), получим:

;

;

;

.

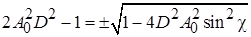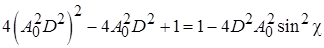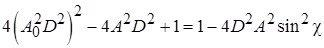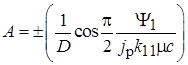Вращающий момент двигателя 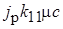больше 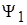– момента возмущения, поэтому автоколебания возможны, когда под синусом и косинусом аргумент .

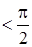Несимметричные вынужденные колебания

Пусть действует возмущающий момент вида:

,

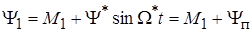где 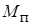– постоянная составляющая момента .

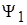Решение ищем как

.

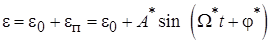Для периодической составляющей:

.

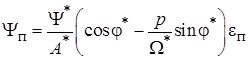Объединив уравнения, получим:

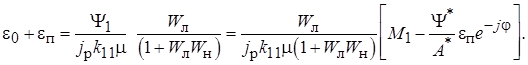(11.14)

Порядок вычисления 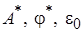следующий:

1. Уравнение (11.14) распадается на два, так как исследуется установившийся режим:

Для постоянной составляющей, где , :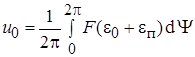

,

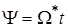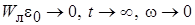тогда

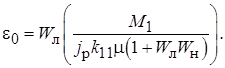
Для переменной составляющей получим уравнение вида (11.13) как в случае симметричного варианта. Отличие только в том, что коэффициенты гармонической линеаризаци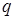и и 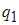зависят не только от амплитуды 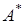и частоты 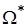, но и от смещения от .

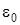2. Далее находятся три неизвестных для заданной частоты 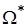возмущения: .

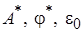Уравнение для переменной составляющей решается графически в соответствии с вышеизложенным:

.

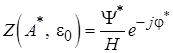Точка пересечения кривой 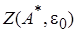с окружностью радиусом 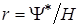дает пару 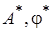, которая должна удовлетворять уравнению постоянных составляющих.