Экспериментальные результаты
Экспериментальная установка и операция
На рисунке 4.15 показана схема экспериментальной установки. Прозрачный цилиндрический сосуд имеет внутренний диаметр D= 200 * 10-3 м. и высоту Н= 390 * 10-3 м. Сосуд находится в водяной рубашке квадратного сечения с целью уменьшения эффекта параллакса в максимально возможной степени. Расстояние от кончика сопла до поверхности 240 * 10-3 м. Одно отверстие сопла, имеющее внутренний диаметр dni = 2.0 * 10-3, наружный диаметр dno= 6.0 * 10-3 м., а высота = 6.5 * 10-3 м. расположено в центре нижней части сосуда. Плоская пластинка вертикально расположена рядом с соплом. Возникновение декартовой системы координат (х, у, z) помещали в центр наконечника сопла.
Рис. 4.15. Экспериментальный аппарат
Частота пузыря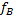 
, задержка газа a, значит пузырь растет со скоростью u-b, и значит пузырь длинной аккорда 
был изменен с помощью двух игл электросопротивления датчика в основном из-за газа, со скоростью потока 
= 41.4 * 10-6 м3/c. Этот газ был выбран потому, что он был использован для предыдущих экспериментальных исследований кипения струи появляющихся от вертикальной плоской пластины. Ранее полученные результаты были использованы, например, для оценки точных новых измерений. Эксперименты повторяли по крайне мере два раза в каждой позиции измерения на y и z плоскостях в зависимости от разброса данных. Среднее значение данных будут представлены в последующих фигурах. Длительность измерения была 360 с в горизонтальной области в диапазоне от y= 1 * 10-3 до 3 * 10-3 м., и 120 с для остальных позиций измерений, расположенных от y > 3 * 10-3 м 
Наружный край области интереса был расположен там, где было больше, чем десять пузырьков более 120 сек. продолжительностью. Пузырь захвата на поверхности пластины был осмотрен за газ со скоростью потока в диапазоне от = = 10 * 10-6 до 80 * 10-6 м3/с.
Кипящие струи вдоль вертикальной плоской пластины
Продвижение угла контакта Ѳa была измерена с сидячим капельным методом. Были использованы две плоские пластины: медная пластина с Ѳa= 62о (хорошая смачиваемость) и акриловая пластина, покрытая парафином с Ѳa= 104о (плохая смачиваемость).
Экспериментальные результаты
1. Горизонтальное распределение частоты пузырьков задержки газа.
Горизонтальное распределение частот пузырьков 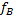измеряется на четырех осевых положениях, z = 50 * 10-3, 100 * 10-3, 150 * 10-3 и 200 * 10-3 м., это видно на рисунке 4.16. На оси абсцисс представлен в логарифмическом масштабе, чтобы усилить поведение пузырьков вблизи стенки. В непосредственной близости от пластины при z= 50 * 10-3 м. плохо смоченная пластина немного меньше, чем результаты для пластины с хорошей смачиваемостью. Существует небольшая разница между горизонтальными распределениями для двух пластин на другом аксиальном измерении 
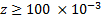м.
Рисунок 4.16 - Горизонтальные распределения частот для пузырька = 41.4 * 10-6 м3/с
Рисунок 4.17 показывает, что при 
м и 
м, измеренный газовый затор больше для слабо увлажненной пластины, чем у пластины с хорошей смачиваемостью. Тем не менее, эта тенденция изменилась в горизонтальной области между примерно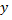 
= 
и 
м, в том же аксиальном положении. Значения α почти те же самые для двух пластин при ˃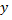 
м. Разница между результатами для двух пластин значительно уменьшается при 
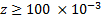м. Следовательно, смачиваемость вертикальной плоской пластины имеет небольшой эффект на горизонтальное распределение для м.
Вертикальные распределения 
и 
приведены на рис. 4,18, где нижний индекс max обозначает максимальное значение. Смачиваемости двух пластин имеет себе ощутимое влияние на распределение осевой и за исключением м. Результаты для пластины хорошей смачиваемости может быть соотнесены, как
(4.8)
(4.9)
Две шкалы длины, 
и 
, может быть определено для характеристики горизонтального распределение 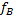, как показано на рис. 4.19. Те, для горизонтального распределения газового затора α, обозначенной 
и 
, аналогично определяются как в Рис. 4.19.
Вертикальные распределения , , и показаны на рис. 4.20 и 4.21. Эти величины существенно не зависит от смачиваемости пластин в любом осевом положении и может быть аппроксимирована таким образом:
(4.10)
(4.11)
(4.12)
(4.13)
Очевидно, что составляет примерно вдвое больше, чем . Такое же
имеет место соотношение между и . Там нет четкого объяснения линейной зависимости четырех величин от осевого расстояния Z.