Краткие теоретические сведения. Типовыми динамическими звеньями называются простейшие составные части систем автоматического управления

Типовыми динамическими звеньями называются простейшие составные части систем автоматического управления, поведение которых описывается обыкновенными дифференциальными уравнениями не выше второго порядка:

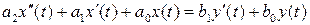, (2.1)

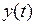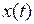где и соответственно входное воздействие и выходной сигнал;

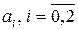и 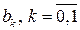– постоянные коэффициенты.

В теории автоматического управления альтернативой дифференциальным уравнениям является аппарат передаточных функций, для получения которых используется преобразование Лапласа.

Оригиналом функции называется функция во временной области, например, 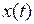. Изображением функции 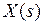является результат преобразования по Лапласу оригинала функции .

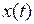Основные свойства преобразования Лапласа:

1) Преобразование оригинала функции

.

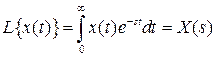2) Обратное преобразование изображения функции

.

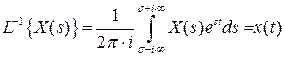3) Линейность

.

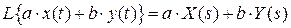4) Умножение аргумента функции на некоторое число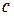

.

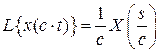5) Преобразование интеграла оригинала функции

.

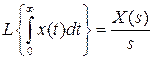6) Преобразование производной оригинала функции

.

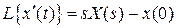7) Преобразование старшей производной оригинала функции

.

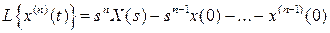Применение преобразования Лапласа к левой и правой частям выражения (2.1) с использованием вышеприведенных свойств позволяет получить следующие выражения

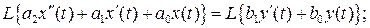
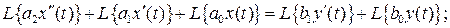
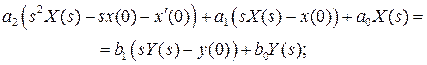
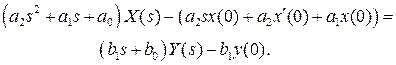
Пусть начальные условия системы в момент времени 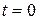являются нулевыми, т.е. система находится в начале координат и ее скорость нулевая. Тогда в последнем выражении в левой и правой частях становятся нулевыми слагаемые, зависящие от начальных условий

.

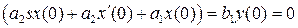Это позволяет существенно упростить выражение

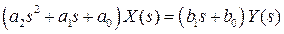(2.2)

Если предположить, что входное воздействие и полином в левой части ненулевые, то разделив на них левую и правую части уравнения, получим следующее выражение

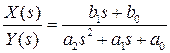
Последнее выражение носит название передаточной функции системы.

Определение 2.1.Передаточной функцией системы 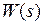называется отношение изображения по Лапласу выходного сигнала к изображению по Лапласу входного воздействия при нулевых начальных условиях

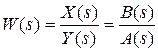, (2.3)

где 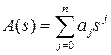– полином знаменателя системы;

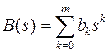– полином знаменателя системы.

Следует заметить, что в случае ненулевых начальных условий выражение теряет свою стройность, и работа с ним становится намного сложнее.

Для физической реализуемости звена необходимо, чтобы степень полинома числителя была не меньше степени полинома знаменателя .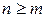

Динамические свойства звеньев определяются по их реакции на типовое входное воздействие. Наиболее простым типовым воздействием является единичная ступенчатая функция 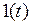(функция Хевисайда), удовлетворяющая условиям

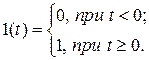(2.4)

Реакция звена на функцию 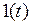называется переходной характеристикой 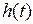– изменение выходной переменной во времени при подаче на вход звена единичной ступенчатой функции 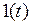. Переходная характеристика представляет собой переход системы от одного равновесного состояния или установившегося режима к другому.

Для определения аналитического выражения переходной характеристики можно воспользоваться соотношением.

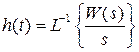. (2.5)

Другим типовым сигналом является дельта-функция Дирака 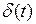, которая описывается следующим образом

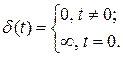(2.6)

Реакция системы на дельта-функцию (импульс) называется импульсной переходной функцией. Она обозначается 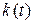. Данная функция связана с переходной функцией соотношением

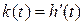. (2.7)

Аналогичным соотношением связаны и порождающие их сигналы

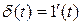. (2.8)

Для анализа в частотной области используется периодический сигнал – синусоида с известными параметрами: частотой, амплитудой и фазой.

Амплитудно-частотная характеристика 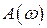представляет собой зависимость коэффициента усиления системы от частоты. Фазо-частотная характеристика 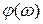представляет собой зависимость сдвига фазы между выходным и входным сигналами от частоты

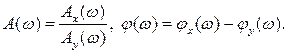(2.9)

Амплитудно-фазовая частотная характеристика представляет собой годограф (диаграмма Найквиста), который описывает передаточная функция системы в частотной области.

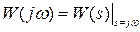. (2.10)

Еще одной типовой частотной характеристикой является логарифмическая амплитудно-частотная характеристика (диаграмма Боде), описываемая следующим выражением

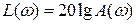. (2.11)

Еще одной важной характеристикой системы является диаграмма расположения нулей и полюсов системы. Нули – это корни характеристического полинома числителя системы 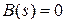. Полюса – это корни характеристического полинома знаменателя системы 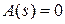. Полюса системы определяют устойчивость системы. Если полюса имеют отрицательную действительную часть, то они называются левыми, т.к. находятся в левой комплексной полуплоскости. Если полюса имеют положительную действительную часть – правыми. Если нулевую – нейтральными. Корни могут быть действительными или комплексно-сопряженными. В последнем случае это порождает в системе колебания переходной характеристики.

Если все полюса системы являются левыми, то система является устойчивой, ее переходная характеристика будет сходиться к некоторому установившемуся значению. Если хотя бы один полюс является правым, то система является неустойчивой, ее переходная характеристика будет иметь расходящийся характер. Если имеется нейтральный полюс, а все остальные полюса являются левыми, то система находится на границе устойчивости. В переходной характеристике такой системы будет иметь место незатухающий колебательный процесс.

К типовым динамическим звеньям относятся пропорциональное звено, интегрирующее звено, апериодическое звено первого порядка, дифференцирующее (реальное дифференцирующее) звено, колебательное звено и его модификации (консервативное звено, апериодическое звено второго порядка).

1) Передаточная функция пропорционального (усилительного) звена

,

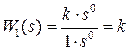где 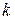– здесь и далее, коэффициент усиления.

В области оригиналов функций это описание соответствует уравнению

.

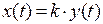2) Передаточная функция интегрирующего звена (интегратора)

.

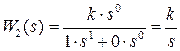Соответствующее описание во временной области имеет вид интеграла

.

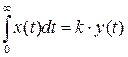3) Передаточная функция апериодического звена первого порядка

,

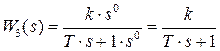где 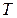– постоянная времени апериодического звена.

Этой функции соответствует дифференциальное уравнение первого порядка

.

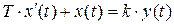Подобное же описание имеет, например, динамика работы конденсатора.

4) Передаточная функция идеального дифференцирующего звена

.

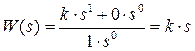Этой функции соответствует дифференциальное уравнение первого порядка

.

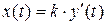Однако, в силу того, что нарушается требование физической реализуемости, данное звено реализуется лишь в ограниченном диапазоне параметров. На практике вместо него используется реальное дифференцирующее звено, описываемое следующей передаточной функцией

.

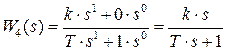Этой функции соответствует дифференциальное уравнение первого порядка

.

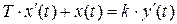5) Передаточная функция колебательного звена

,

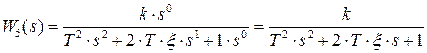где 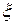– (греч. кси) коэффициент демпфирования.

Данной функции соответствует дифференциальное уравнение второго порядка

.
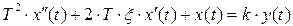