Квантовая природа излучения
Основные законы и формулы
· Скорость света в среде
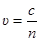
где с – скорость света в вакууме;
n – показатель преломления среды (абсолютный).
· Оптическая длина пути, проходимого световым лучом в однородной среде с показателем преломления n
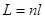 ,
,
где l – геометрическая длина пути световой волны.
· Оптическая разность хода двух световых волн (лучей)
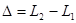 .
.
· Условие максимального усиления света при интерференции (интерференционный максимум)
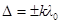 (k=0,1,2,3,…),
(k=0,1,2,3,…),
где λ0 – длина световой волны в вакууме.
Условие максимального ослабления света (интерференционный минимум)
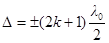 (k=0,1,2,3,…).
(k=0,1,2,3,…).
· Оптическая разность хода световых лучей отражённых от двух поверхностей тонкой пластинки (плёнки), по обе стороны которой находятся одинаковые среды
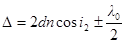 ,
,
или 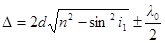 ,
,
где d – толщина пластинки (плёнки);
n – показатель преломления (абсолютный) вещества пластинки;
i1 – угол падения;
i2 – угол преломления света в плёнке.
· Радиусы тёмных колец Ньютона в отражённом свете
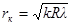 (k=0,1,2,3,…).
(k=0,1,2,3,…).
Радиусы светлых колец Ньютона в отражённом свете
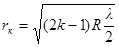 (k=0,1,2,3,…).
(k=0,1,2,3,…).
где k – порядковый номер кольца (k = 0 соответствует центральному тёмному пятну);
R – радиус кривизны линзы;
l – длина световой волны в среде между линзой и пластинкой.
· Условия дифракционных максимумов и минимумов от одной щели
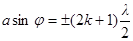 (k=1,2,3…);
(k=1,2,3…);
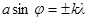 (k=1,2,3…),
(k=1,2,3…),
где а – ширина щели;
k – порядковый номер;
j – угол дифракции.
· Условие главных максимумов дифракционной решётки
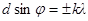 (k=1,2,3…),
(k=1,2,3…),
где d – постоянная (период) дифракционной решётки,
j – угол дифракции.
· Разрешающая способность (сила) дифракционной решётки
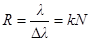 ,
,
где Dl – наименьшая разность длин волн двух соседних спектральных линий (l и l+Dl), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решетки;
N – полное число щелей решётки;
k – порядок спектра.
· Формула Вульфа – Брэггов
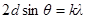 (k=1,2,3…),
(k=1,2,3…),
где θ – угол скольжения (угол между направлением параллельного пучка рентгеновского излучения, падающего на кристалл, и атомной плоскостью в кристалле);
d – расстояние между атомными плоскостями кристалла.
· Степень поляризации света
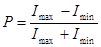 ,
,
где Imax и Imin – максимальная и минимальная интенсивности света, соответствующие двум взаимно перпендикулярным направлениям световых колебаний в луче.
· Закон Брюстера
tg iB = 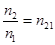 ,
,
где i – угол падения, при котором отразившийся от границы раздела двух диэлектриков луч полностью поляризован;
n21 – относительный показатель преломления второй среды относительно первой.
· Закон Малюса
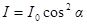 ,
,
где I0 – интенсивность плоскополяризованного света, падающего на анализатор;
I – интенсивность этого света после анализатора;
α – угол между главными плоскостями поляризации (пропускания) поляризатора и анализатора.
· Угол вращения (поворота) плоскости поляризации монохроматического света при прохождении через оптически активное вещество:
а) 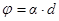 (в кристаллах твердых тел),
(в кристаллах твердых тел),
где α – постоянная вращения;
d – длина пути, пройденного светом в оптически активном веществе;
б) 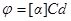 (в растворах),
(в растворах),
где [α] – удельное вращение;
С – массовая концентрация оптически активного вещества в растворе.
· Закон Стефана – Больцмана
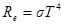
где Re – энергетическая светимость (излучательность) абсолютно чёрного тела;
s – постоянная Стефана – Больцмана;
T – термодинамическая температура Кельвина.
Если излучаемое тело не является абсолютно чёрным (серое тело), то
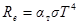
где αт – коэффициент поглощения (коэффициент излучения) серого тела. Эта величина, равная отношению потока излучения 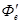 , поглощённого данным телом, к потоку излучения
, поглощённого данным телом, к потоку излучения 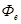 , падающего на это тело:
, падающего на это тело:
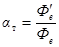 ,
,
зависит от природы тела и его температуры.
Поток излучения 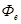 есть энергия, испускаемая телом в единицу времени. (
есть энергия, испускаемая телом в единицу времени. ( 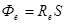 , где S – площадь поверхности излучателя).
, где S – площадь поверхности излучателя).
· Закон смещения Вина:
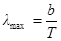 ,
,
где λmax – длина волны, на которую приходится максимум энергии излучения;
b = 2,9·10-3 м·К – постоянная смещения Вина.
· Второй закон Вина: максимальное значение спектральной плотности энергетической светимости 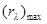 абсолютно черного тела пропорционально пятой степени абсолютной температуры
абсолютно черного тела пропорционально пятой степени абсолютной температуры
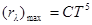 ,
,
где С = 1,29×10-5 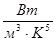 – постоянная Вина.
– постоянная Вина.
· Формула Планка для спектральной плотности энергетической светимости абсолютно черного тела, нагретого до абсолютной температуры Т
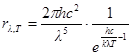 ,
,
или 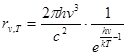 ,
,
где h=6,63×10-34 Дж×с – постоянная Планка,
с=3×108 м/с – скорость света в вакууме,
e – основание натуральных логарифмов,
k=1,38×10-23 Дж/K – постоянная Больцмана.
· Энергия фотона
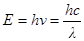 , или
, или 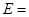 ћω,
ћω,
где ћ 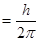 – постоянная Планка;
– постоянная Планка;
n – частота фотона;
w=2pn – циклическая частота.
· Масса фотона
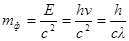 ,
,
где с – скорость света в вакууме;
λ – длина волны фотона.
· Импульс фотона
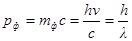 .
.
· Уравнение Эйнштейна для внешнего фотоэффекта
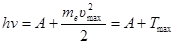 ,
,
где hv – энергия фотона, падающего на поверхность металла;
А – работа выхода электрона;
Т – максимальная кинетическая энергия фотоэлектрона.
· Красная граница фотоэффекта
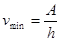 , или
, или 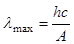 ,
,
где 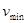 – минимальная частота света, при которой еще возможен фотоэффект;
– минимальная частота света, при которой еще возможен фотоэффект;
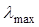 – максимальная длина волны света, начиная с которой фотоэффект прекращается.
– максимальная длина волны света, начиная с которой фотоэффект прекращается.
· Давление света при нормальном падении на поверхность
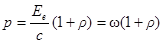 ,
,
где Ее – энергетическая освещенность (облученность) поверхности;
w – объемная плотность энергии излучения;
с – скорость света в вакууме;
r – коэффициент отражения.
· Изменение длины волны при эффекте Комптона
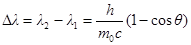 ,
,
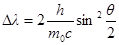
где λ1 – длина волны падающего фотона;
λ2 – длина волны рассеянного фотона;
θ – угол рассеяния фотона после столкновения с частицей;
m0 – масса покоящейся частицы.
Величина 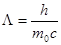 называется комптоновской длиной волны. При рассеянии на электроне L = 2,43×10-12 м.
называется комптоновской длиной волны. При рассеянии на электроне L = 2,43×10-12 м.
Примеры решения задач
Пример 1. На стеклянный клин (n=1,5) с малым углом нормально к его грани падает параллельный пучок лучей монохроматического света с длиной волны λ = 0,6 мкм. При этом на отрезке клина длиной l =1 см возникает m=10 темных интерференционных полос. Определить угол клина.
| Дано: | Решение: |
| n=1,5 λ=0,6 мкм=6×10-7 м l=1 см=10-2 м m=10 | Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней грани. Эти отраженные лучи света когерентны. Поэтому на поверхности клина будут наблюдаться |
| α-? |
|
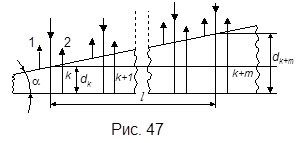 интерференци-онные полосы. Так как угол клина мал, то отраженные лучи 1 и 2 света (рисунок 47) будут практически параллельны. Тем-ные полосы вид-ны на тех участках клина, для которых разность хода лучей кратна нечетному числу половин длин волн:
интерференци-онные полосы. Так как угол клина мал, то отраженные лучи 1 и 2 света (рисунок 47) будут практически параллельны. Тем-ные полосы вид-ны на тех участках клина, для которых разность хода лучей кратна нечетному числу половин длин волн: 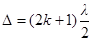 (k=0, ±1, ±2,…) (1)
(k=0, ±1, ±2,…) (1)
Оптическая разность хода световых волн, отраженных от двух поверхностей тонкой пластинки
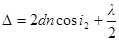 ,
,
где d – толщина пластинки;
i2 – угол преломления света.
Тогда формула (1) примет вид:
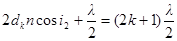 (2)
(2)
где dk – толщина клина в том месте, где наблюдается темная полоса, соответствующая номеру k;
n – показатель преломления стекла.
Согласно условию, угол падения равен нулю; следовательно, и угол преломления i2 равен нулю, а cos i2 = 1. Упростив равенство (2), получим
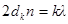 . (3)
. (3)
Пусть произвольной темной полосе k-го номера соответствует толщина dk клина, а темной полосе k+m-го номера – толщина dk+m клина. Тогда (см. рис. 47), учитывая, что m полос укладывается на расстоянии l, найдем:
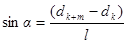 . (4)
. (4)
Так как угол α очень мал, то 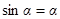 . Выразив из (3)
. Выразив из (3) 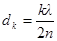 и
и 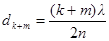 и подставив их в формулу (4), получим:
и подставив их в формулу (4), получим:
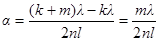 .
.
Произведем вычисления:
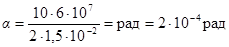 .
.
Но 1 рад = 2,06 . 105 секунд, следовательно
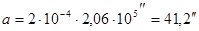
Ответ: искомый угол равен 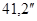 .
.
Пример 2. В просветленной оптике для устранения отражения света на поверхность линзы наносится тонкая пленка вещества с показателем преломления n=1,26, меньшим, чем у стекла. При какой толщине пленки отражение света от линзы не будет наблюдаться? Длина волны падающего света λ = 0,55 мкм, угол падения i=30°.
| Дано: | Решение: |
| n = 1,26 λ= 0,55 мкм =5,5×10-7 м m = 10 | Свет, падая на систему пленка-стекло под углом i, отражается как от верхней I, так и от нижней II поверхности пленки (рис. 48). Лучи S1 и S2 коге- |
| d-? |
рентны, так как образованы из одного луча S. Результат интерференции этих лучей будет зависеть от оптической разности хода. Лучи отражаются от среды с большим показателем преломления, поэтому как на верхней, так и на нижней поверхности пленки происходит потеря полуволны и, следовательно, оптическая разность хода волн равна 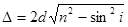 .
.
|
 Условие максимального ослабления освещенности (интерференционный минимум) имеет вид
Условие максимального ослабления освещенности (интерференционный минимум) имеет вид 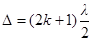 ,
,
|
|
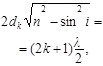
откуда 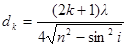 .
.
Полагая k = 1, 2, 3,…, получим ряд возможных значений толщины пленки:
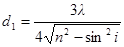 ;
; 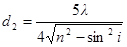 и т.д.
и т.д.
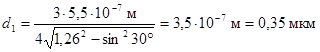 ;
;
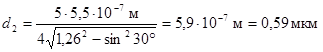 .
.
Ответ: d1= 0,35 мкм; d2= 0,59 мкм и т.д.
|
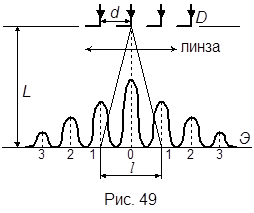 Пример 3. На дифракционную решетку Д нормально падает монохроматический свет с длиной волны λ= 0,65 мкм. На экране Э, расположенном параллельно решетке и отстоящем от нее на расстояние L = 0,5 м, наблюдается дифракционная картина (рисунок 49). Расстояние между дифракционными максимумами первого порядка l=10 см. Определить постоянную дифракционной решетки d и общее число главных максимумов N, получаемых с помощью этой решетки.
Пример 3. На дифракционную решетку Д нормально падает монохроматический свет с длиной волны λ= 0,65 мкм. На экране Э, расположенном параллельно решетке и отстоящем от нее на расстояние L = 0,5 м, наблюдается дифракционная картина (рисунок 49). Расстояние между дифракционными максимумами первого порядка l=10 см. Определить постоянную дифракционной решетки d и общее число главных максимумов N, получаемых с помощью этой решетки. | Дано: | Решение: |
| λ= 0,65 мкм = 6×10-7 м L= 0,5 м l= 10 см = 0,10 м k= 1 | Условие главных максимумов дифракционной решетки: 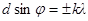 , (1) где d – постоянная дифракционной решетки; , (1) где d – постоянная дифракционной решетки; |
| d-? N-? |
j – угол дифракции;
λ – длина волны падающего на решетку монохроматического света;
k – порядок главных дифракционных максимумов.
Так как 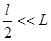 (см. рис. 49), то sin j = tg j =
(см. рис. 49), то sin j = tg j = 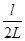 .
.
Тогда получим 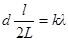 , откуда
, откуда 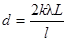 .
.
Подставляя числовые значения величин, получим
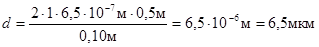
Общее число главных максимумов, даваемых дифракционной решеткой, определяем из условия, что максимальный угол отклонения лучей от нормального направления распространения не может превышать 90°, т.е. sin 90°=1, тогда формула (1) примет вид:
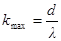 .
.
Общее число максимумов 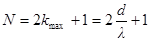 , т. е. влево и вправо от центрального максимума будут наблюдаться по kmax максимумов:
, т. е. влево и вправо от центрального максимума будут наблюдаться по kmax максимумов:
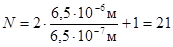 .
.
Ответ: d = 6,15 мкм, N = 21.
Пример 4. Луч света, проходя слой льда, падает на алмазную пластинку, частично отражается, частично преломляется. Определить, каким должен быть угол падения, чтобы отраженный луч был максимально поляризован. Найти степень поляризации отраженного и преломленного света для этого угла падения с помощью формулы Френеля.
| Дано: | Решение: |
| n1=1,31 (лед) n2=2,42 (алмаз) | Согласно закону Брюстера, луч света, отраженный от диэлектрика, максимально поляризован в том случае, если тангенс угла падения численно равен относительному |
| io-? P1-? P2-? |
показателю преломления второй среды относительно первой:
tg 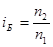 . (1)
. (1)
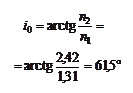
|
|
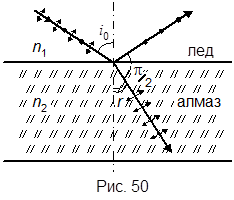 Если i0 = iБ, то отраженный и преломленный лучи взаимно перпендикулярны (рисунок 50). Проходящий свет поляризован лишь частично. Из выражения (1) находим
Если i0 = iБ, то отраженный и преломленный лучи взаимно перпендикулярны (рисунок 50). Проходящий свет поляризован лишь частично. Из выражения (1) находим С помощью формул Френеля определяем степень поляризации отраженного луча:
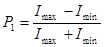 .
.
Здесь 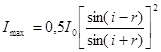 ,
, 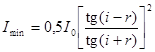 – интенсивности света, распространявшегося в направлениях, перпендикулярном и параллельном плоскости падения;
– интенсивности света, распространявшегося в направлениях, перпендикулярном и параллельном плоскости падения;
I0 – интенсивность естественного света;
i – угол падения;
r – угол преломления.
Если свет падает на диэлектрик под углом полной поляризации (i = i0), то, учитывая, что i0 + r = 90°, для отраженного луча получим 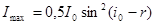 ,
, 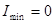 , так как
, так как 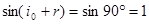 ,
, 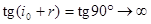 .
.
Степень поляризации отраженного луча
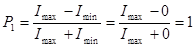 , или
, или 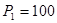 %,
%,
т. е. луч максимально поляризован.
Найдем интенсивности света после преломления в направлениях, перпендикулярном и параллельном плоскости преломления:
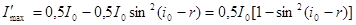 ;
; 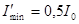 .
.
Степень поляризации преломленного луча:
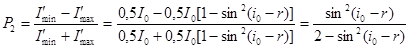
где i0 = 61,5°; r = 90° – i0 = 90° – 61,5° = 28,5°.
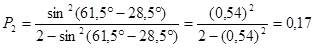 , или
, или 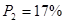
Ответ: i0 = 61,5°; P1 = 100%; P2 = 17%.
Пример 5. Два николя N1 и N2 расположены так, что угол между их плоскостями пропускания составляет α=60°. Определить, во сколько раз уменьшится интенсивность I0 естественного света: 1) при прохождении через один николь N1; 2) при прохождении через оба николя. Каждый николь поглощает 5% света, падающего на него. Потери на отражение света не учитывать.
| Дано: | Решение: |
| α = 60° k = 0,05 | 1) Естественный свет, падая на грань призмы Николя (рисунок 51), расщепляется вследствие двойного лучепреломления на два луча: обыкновенный и необыкновенный. Оба луча одинаковы по интенсивности и полностью поляризованы, но во взаимно перпендикулярных плоскостях. |
1) 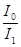 -? 2) -? 2) 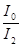 -? -? |
|
|
Обыкновенный луч (о) вследствие полного отражения от границы АВ отбрасывается на зачерненную поверхность призмы и поглощается ею. Необыкновенный луч (е) проходит через призму без отклонения, интенсивность его уменьшается из-за поглощения света призмой на величину kI0. Таким образом, интенсивность света, прошедшего через поляризатор (через первую призму N1), равна
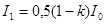 ,
,
где k – коэффициент поглощения света в призме (k = 0,05);
I0 – интенсивность естественного света, падающего на поляризатор.
Относительное уменьшение интенсивности света при прохождении через первый николь N1 равно:
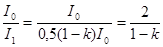 (*)
(*)
Произведем вычисления:
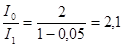 .
.
Таким образом, интенсивность уменьшается в 2,1 раза.
2) Плоскополяризованный пучок света интенсивности I1 падает на второй николь N2 – анализатор и также расщепляется на два луча различной интенсивности: обыкновенный и необыкновенный. Обыкновенный пучок полностью поглощается призмой, поэтому интенсивность его нас не интересует. Интенсивность I2 необыкновенного луча, вышедшего из призмы N2 (анализатора) определяется законом Малюса (без учета поглощения света в анализаторе):
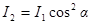 ,
,
где α – угол между плоскостями поляризации поляризатора (N1) и анализатора (N2).
Учитывая потери интенсивности на поглощение во втором николе, получаем:
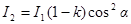 .
.
Искомое уменьшение интенсивности света при прохождении его через оба николя равно:
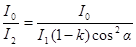 .
.
Заменяя отношение  его выражением по формуле (*), получаем:
его выражением по формуле (*), получаем:
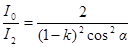 .
.
Произведем вычисления:
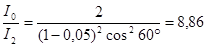 .
.
Итак, после прохождения света через два николя интенсивность его уменьшится в 8,86 раза.
Пример 6. Плоскополяризованный монохроматический пучок света падает на поляроид и полностью им гасится. Когда на пути пучка поместили кварцевую пластинку, интенсивность I пучка света после поляроида стала равна половине интенсивности I0 пучка, падающего на поляроид. Определить минимальную толщину кварцевой пластинки. Поглощением и отражением света поляроидом пренебречь, постоянную вращения α кварца принять равной 48,9 град/мм.
| Дано: | Решение: |
I = 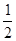 I0 α = 48,9 град/мм I0 α = 48,9 град/мм | Полное гашение света поляроидом означает, что плоскость пропускания поляроида (штриховая линия на рисунке 52) перпендикулярна плоскости колебаний (I – I) плоскополяризованного света, па- |
| d-? |
дающего на него. Введение кварцевой пластины приводит к повороту плоскости колебаний света на угол
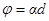 ,
,
где d – толщина пластины.
Угол между плоскостью пропускания поляроида и новым направлением (II – II) плоскости колебаний падающего на поляроид плоскополяризованного света
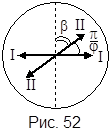
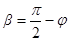 .
.
Воспользуемся законом Малюса
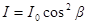 , или
, или 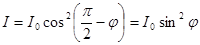 .
.
Откуда 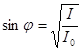 , а
, а 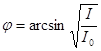 .
.
Тогда получим: 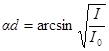 , откуда
, откуда 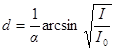 .
.
Произведем вычисления во внесистемных единицах:
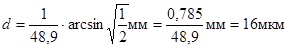 .
.
Ответ: d =16 мкм.
Пример 7. Во сколько раз увеличится мощность излучения абсолютно черного тела, если максимум энергии излучения передвинется от красной границы (λкр = 0,76 мкм) видимого спектра к его фиолетовой границе (λф = 0,38 мкм)?
| Дано: | Решение: |
| λкр = 0,76 мкм = 7,6×10-7 м λф = 0,38 мкм = 3,8×10-7 м | Длина волны, на которую приходится максимум энергии излучения абсолютно черного тела, определяется из закона смещения Вина: |
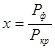 -? -? |
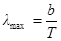 , (1)
, (1)
где Т – термодинамическая температура излучателя;
b = 2,9×10-3 м×K – постоянная Вина.
По формуле (1) определяем температуру излучателя, соответствующую красной и фиолетовой границам видимой области спектра:
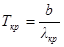 ;
; 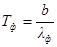 .
.
Мощность излучения абсолютно черного тела
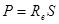 ,
,
где Rе – энергетическая светимость абсолютно черного тела;
S – площадь поверхности излучающего тела.
В соответствии с законом Стефана-Больцмана
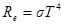 ,
,
где s – постоянная Стефана-Больцмана.
Тогда для красной и фиолетовой границ видимой области спектра
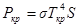 , а
, а 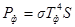 .
.
Следовательно,
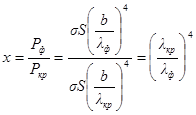 .
.
Произведем вычисления:
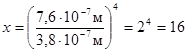 .
.
Ответ: Мощность излучения увеличится в 16 раз.
Пример 8. Определить с помощью формулы Планка энергетическую светимость DRe абсолютно черного тела, приходящуюся на узкий интервал длин волн Dλ = 10Å, соответствующий максимуму спектральной плотности энергетической светимости при температуре тела Т = 3000 K.
| Дано: | Решение: |
| Dλ = 10Å =10×10-10 м Т = 3000 K | Спектральная плотность энергетической светимости абсолютно черного тела характеризует распределение энергии в |
| DRe -? |
спектре излучения тела по длинам волн и выражается формулой 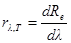 , где dRe – энергетическая светимость, приходящаяся на интервал длин волн от λ до λ+d λ. Отсюда следует, что
, где dRe – энергетическая светимость, приходящаяся на интервал длин волн от λ до λ+d λ. Отсюда следует, что
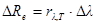 ,
,
где 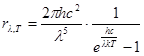 – формула Планка.
– формула Планка.
Используя закон смещения Вина 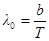 , формулу Планка можно записать так:
, формулу Планка можно записать так:
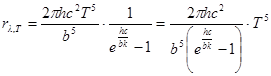 ,
,
или 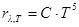 .
.
Эту формулу иногда называют вторым законом Вина. Константа 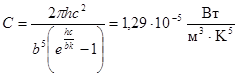 . Тогда расчетная формула
. Тогда расчетная формула 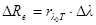 примет упрощенный вид:
примет упрощенный вид:
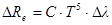 .
.
Подставив числовые значения величин, получим:
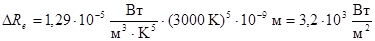
Ответ: DRe = 3,2 кВт/м2.
Пример 9. Определить максимальную скорость 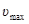 фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ1 = 0,155 мкм; 2) γ-излучением с длиной волны λ2=1 пм.
фотоэлектронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ1 = 0,155 мкм; 2) γ-излучением с длиной волны λ2=1 пм.
| Дано: | Решение: | ||
2) λ2 = 1 пм = 1×10-12 м | Максимальную скорость фотоэлектронов можно определить из уравнения Эйнштейна для фотоэффекта: | ||
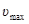 -? -? |
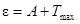 , (1)
, (1)
где 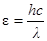 – энергия фотонов, падающих на поверхность металла;
– энергия фотонов, падающих на поверхность металла;
А – работа выхода электрона из металла;
Тmax – максимальная кинетическая энергия фотоэлектронов.
Скорость фотоэлектрона зависит от энергии фотона, вызывающего фотоэффект: если энергия ε фотона много меньше энергии покоя Е0 электрона, то кинетическую энергию фотоэлектрона можно найти по классической формуле:
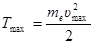 , (2)
, (2)
если же энергия ε фотона сравнима по величине с энергией покоя Е0 электрона, то кинетическую энергию фотоэлектронов необходимо вычислять по релятивистской формуле
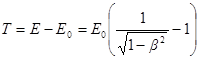 , где
, где 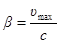 . (3)
. (3)
1) Вычислим энергию фотона ультрафиолетового излучения по формуле:
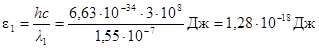 ,
,
или 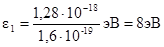 .
.
Полученная энергия фотона (8 эВ) много меньше энергии покоя электрона (Е0 = 0,51 МэВ). Следовательно, кинетическая энергия фотоэлектрона может быть выражена по классической формуле (2):
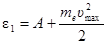 , откуда
, откуда 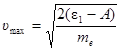 ,
,
где А = 7,5×10-19 Дж = 4,7 эВ – работа выхода электронов из серебра.
Произведем вычисления:
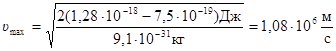
2) Вычислим энергию фотона γ-излучения:
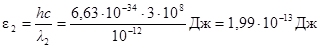 ,
,
или 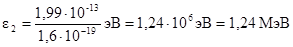 .
.
Работа выхода электрона (А = 4,7 эВ) пренебрежимо мала по сравнению с энергией фотона (ε2 = 1,24 МэВ), поэтому можно принять, что максимальная кинетическая энергия электрона равна энергии фотона: Тmax = ε2 = 1,24 МэВ. В данном случае для вычисления скорости фотоэлектрона следует взять релятивистскую формулу кинетической энергии (3). Из этой формулы найдем
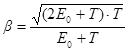 .
.
Заметив, что 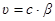 и Тmax = ε2, получим
и Тmax = ε2, получим
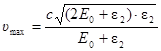 .
.
Произведем вычисления:
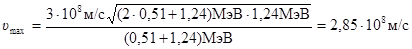
Ответ: 1) 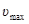 = 1,08×106 м/с; 2)
= 1,08×106 м/с; 2) 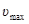 = 2,85×108 м/c.
= 2,85×108 м/c.
Пример 10. Угол рассеяния фотона с энергией ε1 = 1,2 МэВ на свободном электроне θ = 60°. Найти длину волны рассеянного фотона, энергию и импульс электрона отдачи. Кинетической энергией электрона до соударения пренебречь.
| Дано: | Решение: |
| ε1 = 1,2 МэВ = 1,92×10-13 Дж θ = 60° | Изменение длины волны фо-тона при комптоновском рассеянии равно |
| λ2-? Те-? Ре-? |
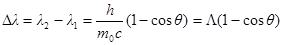 , (1)
, (1)
где λ1 и λ2 – длины волн падающего и рассеянного фотонов;
h = 6,63-34 Дж×с – постоянная Планка;
m0 = 9,11×10-31 кг – масса покоя электрона;
с = 3×108 м/с – скорость света в вакууме;
L = 2,43×10-12 м – комптоновская длина волны электрона;
θ – угол рассеяния (рис. 53).
На рисунке  и
и  – импульсы падающего и рассеянного фотонов. Из формулы (1) находим:
– импульсы падающего и рассеянного фотонов. Из формулы (1) находим:
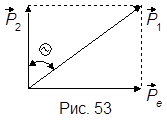
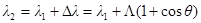 .
.
Так как 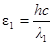 , то получим:
, то получим:
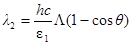 . (2)
. (2)
Энергия электрона отдачи по закону сохранения энергии равна Те = ε1 – ε 2, где ε 2 – энергия рассеянного фотона.
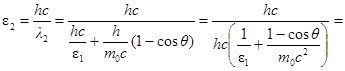
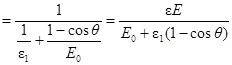 ;
;
Тогда 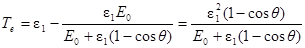 ;
;
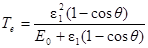 , (3)
, (3)
где Е0 = 0,51 МэВ = 8,2×10-14 Дж – энергия покоя электрона.
Зная энергию электрона, найдем импульс электрона отдачи (релятивистский импульс частицы)
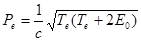 . (4)
. (4)
Подставляя числовые значения в формулы (2), (3) и (4), получаем:
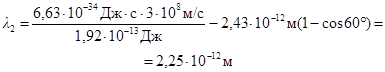
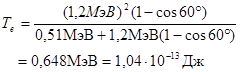
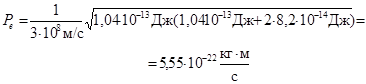
|
Пример 11. На зачерненную поверхность нормально падает монохроматический свет с длиной волны λ = 0,65 мкм, производя давление p=5×10-6 Па. Определить концентрацию фотонов вблизи поверхности и число фотонов, падающих на площадь S = 1 м2 в t = 1 с.
| Дано: | Решение: |
| λ =0,65 мкм = 6,5×10-7 м p = 5×10-6 Па S = 1 м2 t = 1 с | Давление света при нормальном падении на поверхность с коэффициентом отражения ρ вычисляется по формуле |
| n0-? N-? |
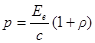 или
или 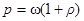 , (1)
, (1)
где Ее – энергетическая освещенность поверхности;
с – скорость света в вакууме;
ω – объемная плотность энергии.
Объемная плотность энергии равна произведению концентрации фотонов (число фотонов в единице объема) на энергию одного фотона:
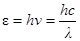 , т.е.
, т.е. 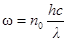 ,
,
откуда 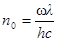 . (2)
. (2)
Из выражения (1) определяем объемную плотность энергии
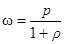 .
.
Тогда 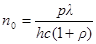 , где ρ = 0 (зачерненная поверхность).
, где ρ = 0 (зачерненная поверхность).
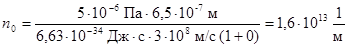 .
.
Число фотонов, падающих на площадь S = 1 м2 в 1 секунду, численно равно отношению энергетической освещенности к энергии одного фотона:
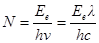 .
.
Из выражения (1) энергетическая освещенность
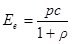 , тогда
, тогда 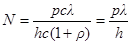 ,
,
так как ρ = 0.
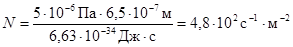
Ответ: n0 = 1,6×1013 м-3; N = 4,8×1021 м -2.

