К выполнению контрольных заданий
К представленным на рецензию контрольным заданиям предъявляются следующие требования:
1. Контрольная работа выполняется каждая в отдельной тетради. В тетради следует оставлять поля шириной не менее 3 см для замечаний рецензента.
2. Основные положения принимаемых решений должны иметь достаточно подробные пояснения.
3. Рисунки, графики, все схемы должны быть выполнены аккуратно и в удобочитаемом масштабе. Масштабы всех графиков должны быть показаны вдоль осей равномерными цифровыми метками. В конце осевых линий графиков указывают отложенную величину измерения и единицы её измерения (графики удобно выполнять на миллиметровой бумаге).
4. Решение каждой задачи должно начинаться с перечерчивания схемы задания индивидуального варианта. В соответствии с вариантом должны быть выписаны все числовые данные задания.
5. Все электрические величины: ЭДС, напряжения, токи, сопротивления и т. д., буквенные обозначения которых указываются в ходе решения, должны быть показаны на схемах, сопровождающих решения задач.
6. Размерность окончательных численных результатов должна быть обязательно указана.
7. Вычисления должны быть сделаны с точностью до четвёртой (не менее) значащей цифры результата.
8. После решения задач необходимо выполнить проверку полученных результатов.
9. Контрольные задания должны быть датированы и подписаны студентом на последней странице решения.
10. Не зачтённое контрольное задание должно быть выполнено заново и прислано на повторную рецензию вместе с первоначальной работой и замечаниями рецензента. Исправление ошибок в отрецензированном тексте не допускается – все исправления следует записывать после первоначального текста под заголовком “Исправление ошибок”.
Контрольные задания зачитываются, если решение не содержит ошибок принципиального характера и учтены все перечисленные требования к выполнению.
Работа над контрольными заданиями позволяет оценить усвоение отдельных разделов курса «ТОЭ», выработать навыки чётко, кратко и аргументировано излагать свои мысли. Для этого целесообразно руководствоваться следующими правилами и принципами:
1. Начиная решение задачи, указать, какие физические законы или расчётные методы предполагается использовать при решении, привести математическую запись этих законов и методов.
2. Тщательно продумать и пояснить, какие буквенные или цифровые обозначения предполагается использовать в решении.
3. В ходе решения не допустимо изменять однажды принятые направления токов и напряжений, наименование узлов схемы, обозначения сопротивлений и других величин.
4. Расчёт каждой величины следует выполнить сначала в общем виде, а затем в полученную формулу подставить численные значения и получить окончательный результат с указанием единиц измерения.
5. Для всех элементов электрических схем следует использовать обозначения, применяемые в учебниках по ТОЭ.
6. Каждому этапу решения необходимо давать пояснения, указывать обоснование принятых действий.
7. Градуировку осей при построении графиков выполнять, начиная с нуля, равномерно через один или два сантиметра. Весь график в целом и отдельные кривые на нём должны иметь названия.
Методические указания к решению задачи 1
Для расчёта линейных электрических цепей синусоидального тока применяют комплексный метод расчёта. Он заключается в том, что изменяющимся по синусоидальному закону функциям времени ставится в соответствие числа комплексного переменного.
Синусоидальным функциям времени тока, напряжения, ЭДС (мгновенным значениям 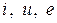 ) ставятся в соответствие комплексные действующие значения этих величин:
) ставятся в соответствие комплексные действующие значения этих величин:
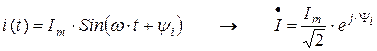 ;
;
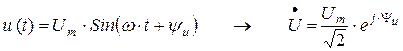 ;
;
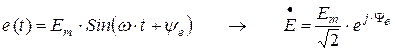 ,
,
где 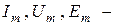 амплитудные значения, соответственно, синусоидальных тока, напряжения и ЭДС;
амплитудные значения, соответственно, синусоидальных тока, напряжения и ЭДС; 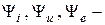 начальные фазы тока, напряжения и ЭДС;
начальные фазы тока, напряжения и ЭДС; 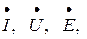 – комплексные действующие значения синусоидальных тока, напряжения и ЭДС.
– комплексные действующие значения синусоидальных тока, напряжения и ЭДС.
Закон Ома для участка электрической цепи в комплексной форме запишется:
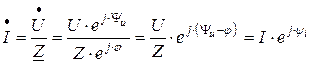 ,
,
где 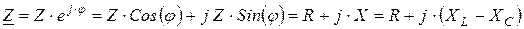 ;
; 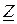 – комплексное сопротивление участка цепи;
– комплексное сопротивление участка цепи;
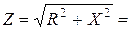
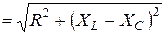 – модуль комплексного сопротивления участка;
– модуль комплексного сопротивления участка;
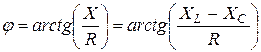 – угол сдвига фаз;
– угол сдвига фаз;
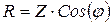 – активное сопротивление участка цепи;
– активное сопротивление участка цепи;
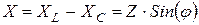 – реактивное сопротивление уча-стка цепи.
– реактивное сопротивление уча-стка цепи.
Активное сопротивление 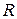 участка электрической цепи учитывает потребление (рассеивание) электрической энергии, реактивные сопротивления
участка электрической цепи учитывает потребление (рассеивание) электрической энергии, реактивные сопротивления 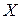 учитывают энергию магнитных (реактивное индуктивное сопротивление
учитывают энергию магнитных (реактивное индуктивное сопротивление 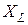 ) или электрических (реактивное ёмкостное сопротивление
) или электрических (реактивное ёмкостное сопротивление 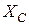 ) полей.
) полей.
Для элементов электрической цепи закон Ома в комплексной форме записывается:
– для резистивного элемента (потребление энергии):
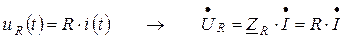 ;
;
– для индуктивного элемента (энергия магнитного поля):
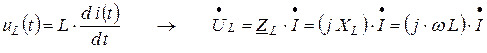 ;
;
– для ёмкостного элемента (энергия электрического поля): 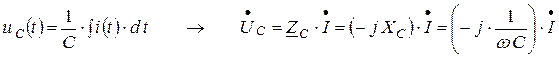 .
.
Здесь: R , L , C – параметры элементов электрической цепи;
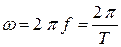 – угловая частота синусоидальных вели чин,
– угловая частота синусоидальных вели чин, 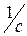 ;
;
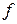 – частота, Гц; Т – период изменения, с.
– частота, Гц; Т – период изменения, с.
Законы Кирхгофа в комплексной форме записываются:
1) закон токов Кирхгофа (ЗТК) – 1-й закон Кирхгофа
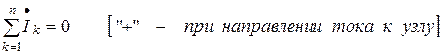 ;
;
2) закон напряжений Кирхгофа (ЗНК) – 2-й закон Кирхгофа
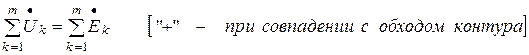 .
.
Пример расчёта.
Заданная электрическая цепь синусоидального тока (вариант №19 из таблицы 1.1) содержит два источника энергии (источника ЭДС), имеет два узла (у = 2) и три ветви (в = 3) (рисунок 1.21).
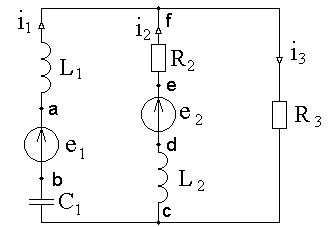
Рисунок 1.21 – Электрическая цепь синусоидального тока
Параметры элементов электрической цепи и источников ЭДС:
| L1, мГн | L2, мГн | C1, мкФ | R2, Ом | R3, Ом | f, Гц |
| 15,92 | 35,81 | 3,978 |
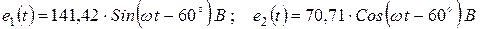 .
.
1. По законам Кирхгофа для расчёта токов ветвей необходимо составить одно уравнение по закону токов [для одного из узлов цепи – 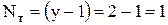 ] и два уравнения по закону напряжений [для двух независимых контуров –
] и два уравнения по закону напряжений [для двух независимых контуров – 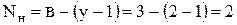 ].
].
а) дифференциальная форма:
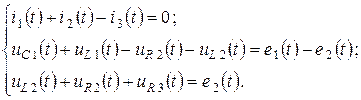
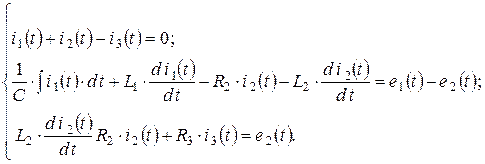
а) комплексная форма:
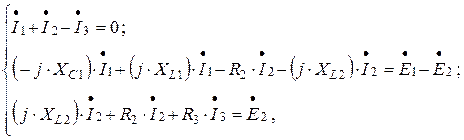
где 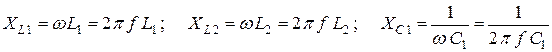 .
.
2. Комплексные действующие значения ЭДС источников в показательной форме записи запишутся:
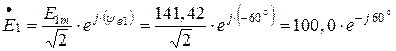 В;
В;
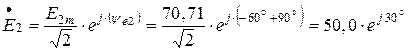 В.
В.
По формуле Эйлера определится алгебраическая форма записи комплексные действующие значения ЭДС источников энергии:
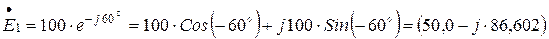 В;
В;
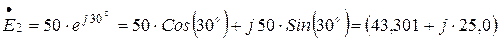 В.
В.
Реактивные сопротивления индуктивностей и ёмкости токам заданной частоты определятся:
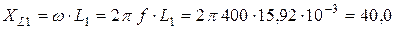 Ом;
Ом;
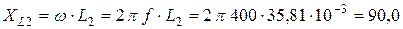 Ом;
Ом;
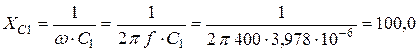 Ом.
Ом.
Для расчёта комплексных действующих значений токов ветвей электрической цепи схема принимает вид, показанный на рисунке 1.22а.
Комплексные сопротивления ветвей электрической цепи (рисунок 1.22а):
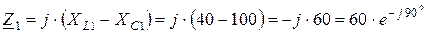 Ом;
Ом; 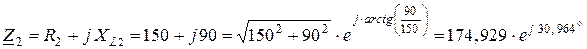 Ом;
Ом;
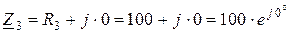 Ом.
Ом.
1) Расчёт действующих значений токов ветвей электрической цепи методом контурных токов.
На основании метода контурных токов для заданной электрической цепи (рисунок 1.22б) необходимо составить два уравнения 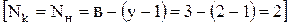 для двух контурных токов
для двух контурных токов 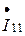 и
и 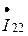 .
.
Задаёмся независимыми контурами и указываем в них произвольно направления их контурных токов 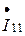 и
и 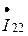 (рисунок 1.22б).
(рисунок 1.22б).
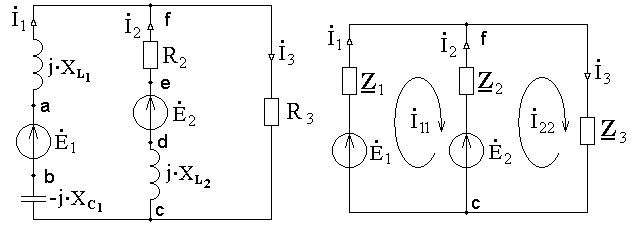
а) б)
Рисунок 1.22 – Расчётная схема электрической цепи
Уравнения для контуров электрической цепи по методу контурных токов запишутся в общем виде (обход контура выбирается совпадающим с направлением собственного контурного тока):
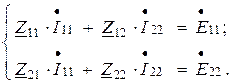
Собственные сопротивления контуров [два одинаковых индекса] – равные арифметической сумме комплексных сопротивлений ветвей, входящих в рассматриваемый контур:
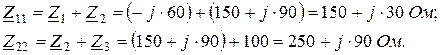
Общие сопротивление смежных контуров [два различных индекса] равны арифметической сумме комплексных сопротивлений ветвей, расположенных между соответствующими контурами. Эти сопротивления положительны, если направления контурных токов смежных контуров в них совпадают (и отрицательны, если не совпадают):
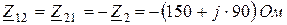 .
.
Контурные ЭДС равны алгебраической сумме комплексных действующих значений ЭДС источников, входящих в контур. Значения ЭДС положительны, если их направления совпадают с направлением собственного контурного тока:
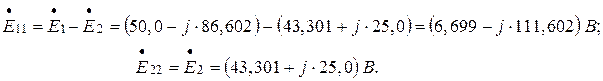
Для определения контурных токов в электрической цепи (рисунок 1.22б) имеем систему уравнений:
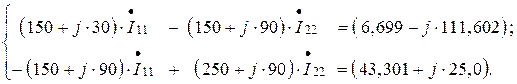
Решение системы уравнений для контурных токов можно найти с помощью программы компьютерной математики MathCAD:
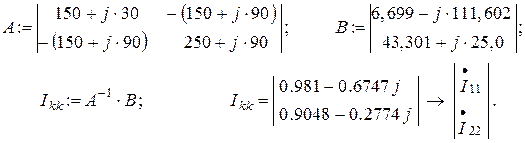
По найденным контурным токам определятся токи в ветвях:
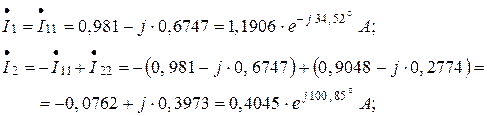
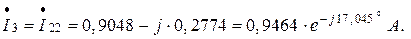
2) Расчёт действующих значений токов ветвей электрической цепи методом узловых потенциалов.
Метод узловых потенциалов основан на применении законов токов Кирхгофа и Ома. По этому методу составляются уравнения для узловых потенциалов узлов схемы, при условии, что один из узлов цепи принимается за опорный и заземляется (его потенциал принимается равным нулю). Число уравнений, которые необходимо составить для цепи по методу узловых потенциалов на единицу меньше числа узлов схемы: 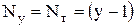 .
.
Заданная электрическая цепь (рисунок 2б) имеет два узла, следовательно, по методу узловых напряжений для цепи необходимо составить одно уравнения для узлового потенциала 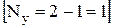 . Если в качестве опорного принять узел схемы «с», уравнение для узлового напряжения
. Если в качестве опорного принять узел схемы «с», уравнение для узлового напряжения 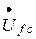 запишется:
запишется:
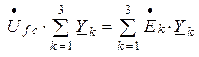 .
.
Здесь: 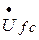 – напряжение узла электрической цепи по отношению к узлу, выбранному за опорный (узел «c »);
– напряжение узла электрической цепи по отношению к узлу, выбранному за опорный (узел «c »);
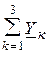 – собственная узловая проводимость узла «f», равная арифметической сумме комплексных проводимостей ветвей, присоединённых к этому узлу;
– собственная узловая проводимость узла «f», равная арифметической сумме комплексных проводимостей ветвей, присоединённых к этому узлу;
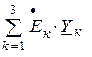 – узловой ток, равный сумме токов короткого замыкания ветвей, подходящих к узлу « f » (алгебраическая сумма произведений комплексных действующих значений ЭДС источников в ветвях на комплексную проводимость этих ветвей; если ЭДС ветви направлена к узлу, то составляющая тока короткого замыкания для ветви записывается со знаком «плюс»).
– узловой ток, равный сумме токов короткого замыкания ветвей, подходящих к узлу « f » (алгебраическая сумма произведений комплексных действующих значений ЭДС источников в ветвях на комплексную проводимость этих ветвей; если ЭДС ветви направлена к узлу, то составляющая тока короткого замыкания для ветви записывается со знаком «плюс»).
Для заданной электрической цепи (рисунок 1.22б) имеем:
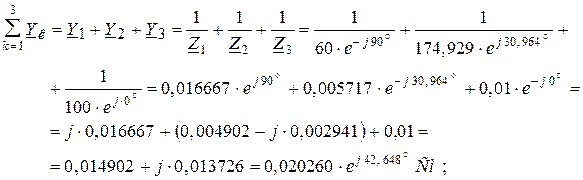
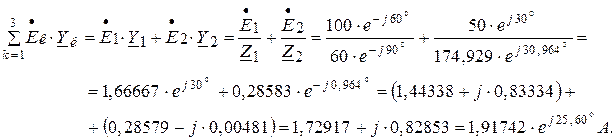
Узловое напряжение электрической цепи относительно опорного узла определится:
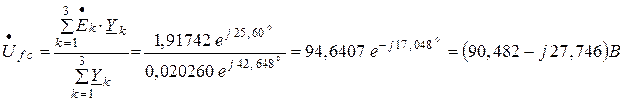 .
.
На основании закона Ома найдутся токи ветвей цепи:
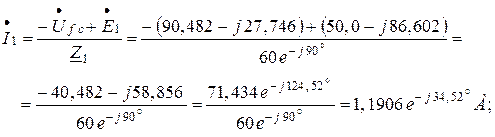
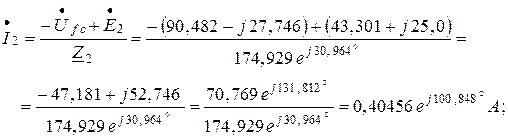
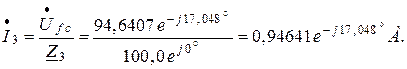
Значения токов ветвей, найденные методом узловых потенциалов совпали со значениями токов, определёнными методом контурных токов.
3. Баланс комплексных, активных и реактивных мощностей источников электрической энергии и приёмников запишется:
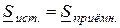 ;
; 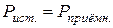 ;
; 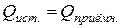 .
.
Комплексная мощность, отдаваемая источниками энергии:
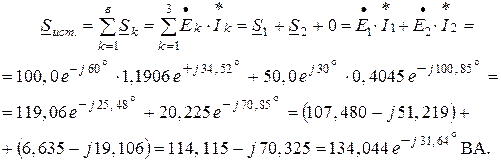
Здесь: 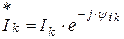 – сопряжённый комплекс тока
– сопряжённый комплекс тока 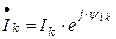 .
.
Активная и реактивная мощности источников энергии:
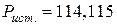 Вт;
Вт; 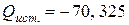 ВАр.
ВАр.
Активная мощность приёмников энергии:
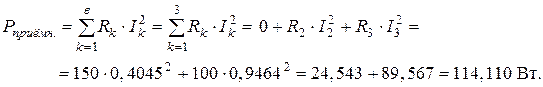
Реактивная мощность приёмников энергии:
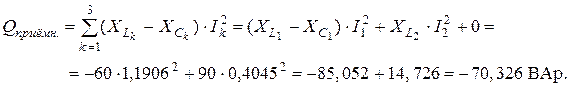
Относительные погрешности выполненного расчёта:
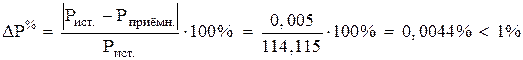 ;
;
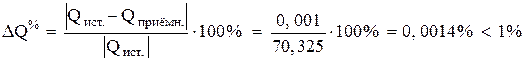 .
.
Расчёт режима электрической цепи выполнен верно, баланс мощностей соблюдается с требуемой точностью.
4. Для построения топографической векторной диаграммы находим комплексные действующие значения напряжений на всех элементах электрической цепи:
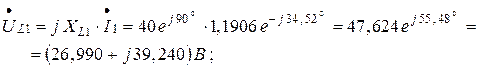
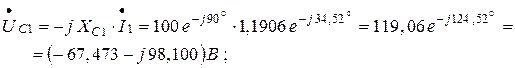
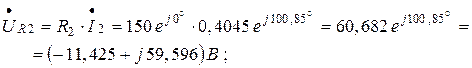
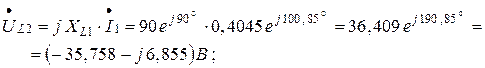
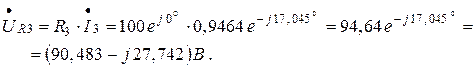
Комплексные потенциалы точек схемы (рисунок 1.22а) при условии, что потенциал точки « а » схемы равен нулю:
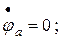
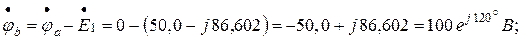
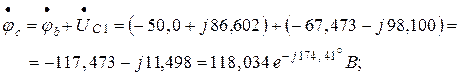
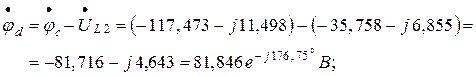
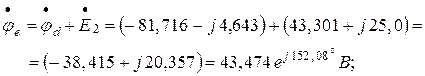
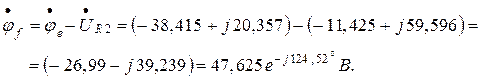
Задаёмся комплексной плоскостью и в масштабе тока  строим векторы токов ветвей. Выбираем масштаб напряжений (потенциалов)
строим векторы токов ветвей. Выбираем масштаб напряжений (потенциалов)  и в этом масштабе строим на комплексной плоскости векторы потенциалов точек схемы (векторы напряжений на элементах электрической цепи).
и в этом масштабе строим на комплексной плоскости векторы потенциалов точек схемы (векторы напряжений на элементах электрической цепи).
Примечание: построение векторов токов, потенциалов (напряжений) удобно выполнять через их проекции на координатные оси комплексной плоскости.
Векторная диаграмма токов и топографическая векторная диаграмма напряжений для заданной цепи (рисунок 1.22а) показана на рисунке 1.23.
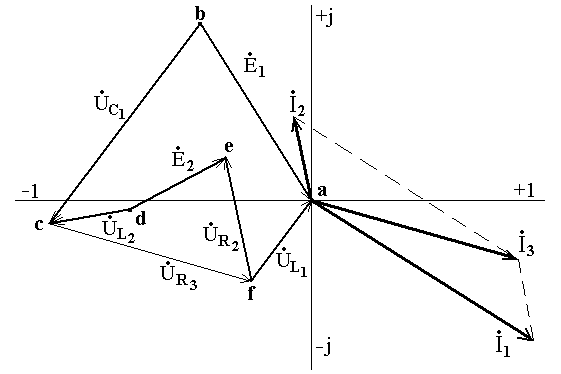
Рисунок 1.23 – Векторная диаграмма токов и топографическая диаграмма напряжений для электрической цепи
5. Полагаем, что между индуктивными катушками 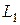 и
и 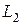 электрической цепи имеется индуктивная связь при взаимной индуктивности
электрической цепи имеется индуктивная связь при взаимной индуктивности 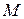 (рисунок 1.24).
(рисунок 1.24).
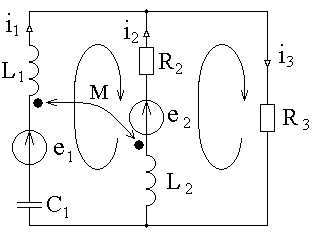
Рисунок 1.24 – Электрическая цепь с взаимной индуктивностью
С учётом направлений токов в ветвях с индуктивностями (рисунок 1.21) указываем одноимённые зажимы индуктивных катушек, обеспечивая их встречное включение (встречное направление в катушках магнитных потоков самоиндукции и взаимной индукции).
По законам Кирхгофа с учётом индуктивной связи электрическая цепь опишется тремя уравнениями.
Дифференциальная форма записи законов Кирхгофа:
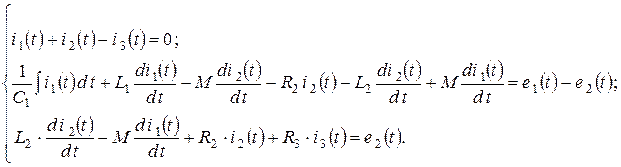
Комплексная форма записи законов Кирхгофа:
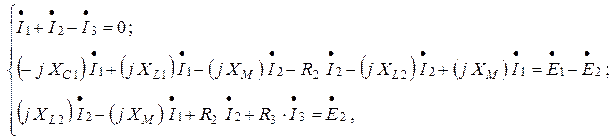
где 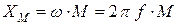 – сопротивление взаимной индуктивности индуктивно-связанных катушек.
– сопротивление взаимной индуктивности индуктивно-связанных катушек.
Методические указания к решению задачи 2
С учётом индивидуального варианта задачи ( №19 из таблицы 2.1) схема заданной электрической цепи, подключенной к трёхфазному генератору, имеет вид, приведённый на рисунке 2.21.
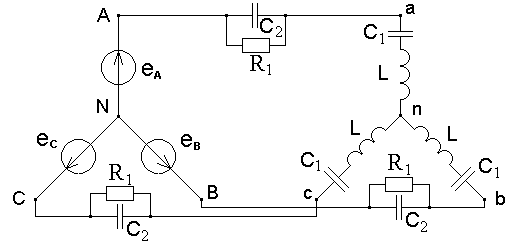
Рисунок 2.21 – Схема трёхфазной электрической цепи
