Б. Для компьютерного тестирования

Казахская Головная Архитектурно-Строительная Академия

Активный раздаточный материал

Математика 1 ФОЕНП

Кредит 3

Лекция №2. «Обратная матрица.

Система линейных уравнений» 1-й семестр

2013-2014 уч. год

Краткое содержание лекции

Обратная матрица

Для каждого числа а≠0, существует обратное число а^-1 такое, что произведение а а^-1=1. Для квадратных матриц тоже вводится аналогичное понятие.

Определение: Матрица А^-1 называется обратной по отношению к квадратной матрице А, если при умножение этой матрицы на данную как справа, так и слева получается единичная матрица:

А^-1 А = А А^-1 =Е

Если определитель матрицы отличен от нуля (| А | ≠ 0 ), то такая квадратная матрица называется невырожденной, или неособенной; в противном случае ( | А | = 0 ) – вырожденной или особенной.

Теорема: (необходимое и достаточное условие существования обратной матрицы). Обратная матрица А^-1 существует (и единственная) тогда и только тогда, когда исходная матрица невырожденная.

Для невырожденных матриц выполняются следующие свойства:

1. 2. ( А^-1 ) ^-1 = А 3. (А^m ) ^-1 = (А^m ) ^-1 4. (АВ) ^-1 =В^-1 А^-1 5. (А^-1 )¹ = (А¹ ) ^-1

Ранг матрицы

Рангом матрицы А, называется наивысший порядок отличных от нуля миноров этой матрицы.

Из определения следует:

а) ранг матрицы А(mxn) не превосходит меньшего из его размеров, т.е. r (A)≤ min (m; n);

б) r(A)=0 тогда и только тогда, когда все элементы матрицы равны нулю, т. е. A =0;

в) для квадратной матрицы n-го порядка r (A)= n тогда и только тогда, когда матрица А- невырожденная.

Теорема.Ранг матрицы не изменяется при элементарных преобразованиях матрицы.

Элементарными преобразованиями называются следующие:

а) отбрасывание нулевой строки (столбца);

б) умножение всех элементов строки (столбца) матрицы на число не равное нулю;

в) изменение порядка строк (столбцов) матрицы;

г)прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;

д) транспонирование матрицы.

Системы линейных уравнений.

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если оно имеет более одного решения.

Запишем систему в матричной форме. Обозначим:

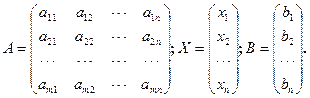
На основании определения умножения и равенства матриц систему можно записать в виде: АХ = В

Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю, т.е. в уравнении B=0, AX=0.

Задание на СРС

1. Решение системы линейных уравнений методом Крамера. [3- cтр.174; 1 – стр. 35]

Форма отчёта: реферат. Срок: 6 дней.

2. Решить задачи ИДЗ-1.2. [3 – стр. ]

Задание на СРСП

1. Теорема Кронекера-Капелли. [1, 3-стр.177]

Контрольные вопросы:

А. Для письменного контроля

1. Что такое обратная матрица? Как находится обратная матрица?
2. Как определяется ранг матрицы? Как определяется транспонированная матрица?
3. Методы решения системы линейных уравнений? Теорема Кронекера-Капелли
4. Решение системы линейных однородных уравнений

Б. Для компьютерного тестирования

1. При каких значениях λ матрица 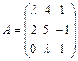не имеет обратной?

А) 0; В) 2; С) -4; 2; Д) -8; 1.

2. Найти ранг матрицы 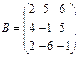. А) 0; В) 1; С) 2; Д) 3.

3. Решить систему уравнения методом Крамера.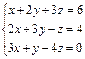

А) (1;1;1); В) (-1;2;3); С) (-1;-1;2); Д) (-1;-1;-1).

Глоссарий

№	На русском языке	На казахском языке	На английском языке
	Обратная матрица	Кері матрица	inverse matrix
	Необходимый	Қажет	indispensable
	Достаточный	Жектілікті	sufficient
	Единственный	Дара	singular
	Система	Жүйе	system
	Линейный	Сызықты	linear
	Уравнение	Теңдеу	equation
	Переменный	Айнымалы	variable
	Решение	Шешуі	decision
	Совместная система	Үйлесімді жүйе	combined system

Список литературы

Основная:

1. К.Кабдыкайыр. Сборник задач по Высшей математике. Учебное пособие. Алматы: «Дәуір», 2007. -408стр.

2. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах: Учебное пособие для втузов.- М.: Оникс, 2007, 2006

3. Байбазаров М.Б., Божанов Е.Т., Уразмагамбетова Э.У .Лекционный курс по математике. Учебное пособие, часть 1. Алматы, КазГАСА, 2003.

4. Индивидуальные задания по высшей математике под общей редакцией доктора физико-математических наук проф. А.П. Рябушко. Учебное пособие. II-часть.Минск, «Высшая школа», 2002г.

Дополнительная:

5. Сыдыкова Д.К. Математика 1. Методическое руководство к выполнению заданий для СРС. Алматы: КазГАСА, 2008.

6. Кремер Н.Ш., Путко Б.А. Высшая математика для экономистов. Учебник. Изд. Объединение «ЮНИТИ»,2006. -479стр.