Поиск в ширину в графе

При поиске в глубинупросмотренные, но еще не использованные вершины скапливались в стеке. Чем позднее была просмотрена вершина, тем раньше ее удаляли из стека. Заменим стек очередью.

Механизм подключения элемента к началу очереди полностью совпадает с вталкиванием в стек (процедура push). Механизм выталкивания из очереди(функции poptail) – первым из очереди удаляется первый попавший туда элемент.

Основная идея поиска в ширину– у вершины v просматриваются и помещаются в очередь сразу всеее новые «соседи», после чего v становится использованной и удаляется из очереди (рис. 8.9).

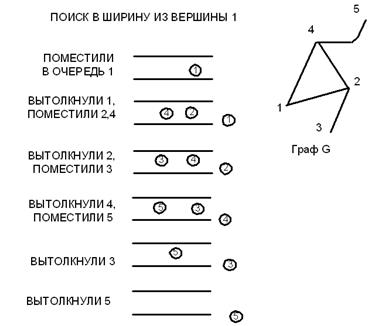
Рис. 8.9. Поиск в ширину из вершины 1

Поиск в ширину можно использовать для нахождения кратчайшего пути между парой фиксированных вершин s и t. Под кратчайшим путеммы понимаем путь с минимальным количеством ребер, так как пока все ребра графа имеют одинаковую длину (можно считать, что все ребра имеют единичную длину). Поскольку мы находим сразу всех соседей, поиск, как волна от источника, равномерно распространяется во все стороны (рис. 8.10). Поэтому в очереди сначала находятся все вершины, удаленные от s на расстояние 1, через некоторое время – все вершины, удаленные на расстояние 2 и т.д. Понятно, что путь, найденный таким образом, будет кратчайшим.

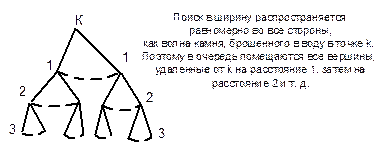
Рис. 8.10. Распространение волны

Процедура поиска в ширину WD:

1 procedure WD(v);

{поиск в ширину с началом в вершине v}

2 begin

3 ОЧЕРЕДЬ:= NIL; ОЧЕРЕДЬ <= v; НОВЫЙ[v]:= ложь;

{v помещается в очередь}

4 while ОЧЕРЕДЬ<>NIL do

5 begin

6 tail <= ОЧЕРЕДЬ;

{выталкивание из очереди нижнего элемента}

7 for u ЗАПИСЬ[tail] do

{ищем всех новых соседей узла tail}

8 if НОВЫЙ[u] then

9 begin

10 ОЧЕРЕДЬ <= u; НОВЫЙ[u]:= ложь

11 end

12 end {while ОЧЕРЕДЬ <>NIL}

13 end;

Как и для поиска в глубину, легко показать, что каждая вершина просматривается ровно один раз и вычислительная сложность равна O(n+m).

Чтобы найти кратчайший путь, нужно немного модифицировать процедуру WD. Во-первых, добавить одномерный массив ПРЕД по числу вершин графа. Пусть во время работы процедуры в вершину u₂ мы попали из u₁: u₁ была предыдущей для u₂, поэтому ПРЕД[u₂]:= u₁. Во-вторых, чтобы массив ПРЕД заполнялся именно так, изменим строку 10 процедуры WD:

9 begin

10 ОЧЕРЕДЬ <= u; НОВЫЙ[u]:= ложь;

ПРЕД[u]:= tail;

Итак, чтобы найти кратчайший путь из s в t, вызовем модифицированную WD(s).

Как только конец пути t попадет в очередь, поиск следует прекратить. Каким образом восстановить путь от s до t из массива ПРЕД?

Рассмотрим последовательность вершин, где u₁ = ПРЕД[u₂]. В t мы попадем из u, в u из v и т.д., пока не встретим s. Эта последовательность – путь из s в t. Первоначальная инициализация массива ПРЕД: ПРЕД[u]:= u.

Вопрос. Как будет заполнен массив ПРЕД при поиске в ширину на рис. 8.9 в момент помещения в очередь вершины 5?

Метод поиска в ширину применим для определения связных компонент графа. Вызвав WD(s), просмотрим все вершины u, для которых существует путь из s в u.

Ответ. ПРЕД[1] = 1; ПРЕД[2] = ПРЕД[3] = 1;

ПРЕД[4] = 3; ПРЕД[5] = 2.

Каркасы графа

Каждый связный граф имеет каркас. Более того, у одного графа может быть несколько разных каркасов. Дадим теперь определение каркаса.

Для произвольного связного графа G=<V, E> любое дерево D=<V, T>, где T Е будет его каркасом (рис. 8.11).

(Напомним, что дерево – произвольный неориентированный связный граф без циклов.)

Другими словами, каркас D соединяет все вершины графа G так, чтобы не было циклов.

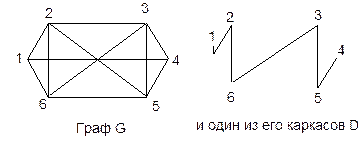
Рис. 8.11. Каркас графа

Ребра каркаса будут называться ветвями, ребра, не вошедшие в каркас, хордами.

Вопрос. Перечислите хорды графа G относительно каркаса D на рис. 8.11.

Каркасы можно строить как поиском в глубину, так и поиском в ширину (рис. 8.12). В обоих случаях достижение новой вершины u из старой v означает включение в каркас ветви (v-u).

АЛГОРИТМ {Нахождение каркаса связного графа методом поиска в глубину}

Данные: Связный граф G=<V, E>, заданный списками инцидентности ЗАПИСЬ[v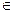], v V.

Результаты: Каркас D=<V, T> графа.

Переменные НОВЫЙ, ЗАПИСЬ, Т – глобальные.

1 procedure GLD(v);

2 begin

3 НОВЫЙ[v]:= ложь;

4 for u 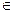ЗАПИСЬ[v] do

5 if НОВЫЙ[u] then {нашли новую ветвь (v–u)}

6 begin

7 T:= T 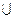(v-u); {и присоединили ее к каркасу}

9 GLD(u)

10 end

11 end;

1 begin {основная программа}

2 for u 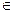V do НОВЫЙ[u]:= истина; {инициализация}

3 T:= 0; {T-множество найденных ветвей}

4 GLD(k) {корень k – произвольная вершина}

5 end.

Докажем корректность этого алгоритма.

Алгоритм строит связный граф, так как каждое новое ребро (v-u) продолжает уже существующий путь от k к v.

Построенный граф не содержит циклов. Каждая новая ветвь (v-u) соединяет уже рассмотренную v с новой u. Чтобы замкнуть цикл, требуется ребро, соединяющее две уже рассмотренные вершины.

Построенный граф содержит все вершины графа G – это свойство поиска в глубину. По этой же причине вычислительная сложность алгоритма О(n+m).

Любой каркас обладает важным свойством – от корня k до произвольной вершины v существует единственный путь, состоящий из ветвей каркаса. Если бы их было два, получился бы цикл, если бы ни одного, каркас не был бы связным.

Кроме того, если каркас D построен поиском в глубину, то для двух вершин u и v, соединенных ребромe 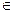E, всегда можно сказать: или v – потомок u, или u – потомок v (относительно каркаса D).

Первое означает, что u лежит на пути из корня k в вершину v, второе – v на пути из k в u. Это легко доказать.

Пусть одна из вершин, например, v, просмотрена раньше u. Построен путь от корня k до v. Процесс поиска в глубину начинается с вершины v. Так как u и v соединены ребром, то рано или поздно будет рассмотрена вершина u и построен путь от v до u. Получился путь k–v–u.

Если v и u соединены ветвью каркаса, то одна из них – сын, другая – отец.

АЛГОРИТМ {Каркас связного графа поиском в ширину}

Данные: связный граф G=<V, E>, представленный списками ЗАПИСЬ[v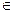], v V.

Результаты: каркас D=<V, T> графа G.

1 begin

2 for u 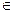V do НОВЫЙ[u]:= истина;{инициализация}

3 T:= 0 {T – множество найденных ветвей}

4 ОЧЕРЕДЬ:= NIL;

5 ОЧЕРЕДЬ <= k; {поместили в очередь корень k}

6 НОВЫЙ[k]:=ложь; {пометили k как просмотренный}

7 while ОЧЕРЕДЬ <> NIL do

8 begin tail <= ОЧЕРЕДЬ;

8 for u 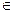ЗАПИСЬ[tail] do

9 if НОВЫЙ[u] then {нашли новую ветвь v–u}

10 begin

11 ОЧЕРЕДЬ <= u; НОВЫЙ[u]:=ложь;

12 T:=T (v-u) {и присоединили ее к каркасу}

13 end

14 end

15 end.

Легко доказать, что этот алгоритм строит каркас произвольного графа за О(n+m) шагов.

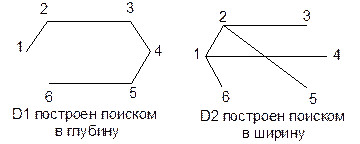
Рис. 8.12. Два каркаса графа G

Если каркас D графа G построен поиском в ширину, то путь от корня k до произвольной вершины v будет не только единственным, но и кратчайшим. Это следует из свойств поиска в ширину.

Ответ. {(2–3), (3–4), (5–6), (6–1), (2–5), (1–4)}.