Раздел 10. Элементы теории вероятностей
1. Предмет теории вероятностей.
2. Элементы комбинаторного анализа ( перестановки, размещения, сочетания).
3. Событие. Пространство элементарных событий. Классификация событий. Алгебра событий.
3. Относительная частота события.
4. Классическое определение вероятности.
5. Геометрическое определение вероятности .
6. Определение условной вероятности. Независимость событий.
7. Вероятность произведения событий.
8. Теоремы сложения и следствия из них.
9. Формула полной вероятности.
10. Вероятность гипотез. Формулы Байеса.
11. Последовательность независимых испытаний, схема Бернулли.
12. Предельные теоремы Муавра-Лапласа и Пуассона.
13. Дискретные и непрерывные случайные величины.
14. Функция распределения и её свойства.
15. Плотность распределения непрерывной случайной величины и её свойства.
16. Числовые характеристики случайной величины (математическое ожидание, дисперсия, среднее квадратическое отклонение).
17. Закон биноминального распределения, закон Пуассона и их числовые характеристики.
19. Нормальный закон распределения.
20. Равномерное распределение.
21. Показательный закон распределения.
Раздел 11. Элементы математической статистики
1. Выборочный метод описания и анализа статистических данных.
2. Статистический вариационный ряд.
3. Интервальные статистические ряды.
4. Графическое представление статистических распределений выборки (полигон, гистограмма).
5. Эмпирическая функция распределения; её основные свойства.
6. Основные числовые характеристики выборки.
7. Начальные и центральные моменты k-го порядка, их использование в статистике.
8. Точечные оценки неизвестных параметров распределения.
9. Интервальные оценки параметров распределения.
10. Доверительная вероятность, доверительный интервал.
11. Статистическая гипотеза. Критерий согласия Пирсона.
13. Корреляционная зависимость.
14. Линейное уравнение регрессии; определение его параметров методом наименьших квадратов.
15. Выборочный коэффициент корреляции; его свойства. Коэффициент детерминации.
Перечень рекомендуемой литературы
Учебники
1. Белько И.В., Кузьмич К.К. Высшая математика для экономистов. Часть 1-3. – Мн.: Новое знание, 2006.
2. Белько И.В., Свирид Г.П. Теория вероятностей и математическая статистика. – Мн.: Новое знание, 2002.
3. Герасимович А.И., Рысюк Н.А. Математический анализ. Ч.1.-Мн.: Выш. школа, 1989.
4. Герасимович А.И., Кеда Н.П., Сугак М.Б. Математический анализ.Ч.2.-Мн.: Выш. школа, 1990.
5. Гурский Е.И. Основы линейной алгебры и аналитической геометрии. -Мн.: Выш. школа, 1982.
6. Красс М.С. Математика в экономике. – М.: ИД ФБК – ПРЕСС, 2005.
7. Мацкевич И.П., Свирид Г.П. Высшая математика. Теория вероятностей и математическая статистика. – Мн.: Выш. школа, 1993.
8. Пискунов Н.С. Дифференциальное и интегральное исчисление. В 2 ч. -М.: Наука, 1987. Ч.1.
9. Пискунов Н.С. Дифференциальное и интегральное исчисление. В 2 ч. -М.: Наука, 1987. Ч.2.
10. Письменный Д. Конспект лекций по высшей математике. 1часть.-М., Айрис Пресс,2004
11. Письменный Д. Конспект лекций по высшей математике. 2часть.-М., Айрис Пресс,2004
Задачники
12. Гурский Е.И. Руководство к решению задач по высшей математике. В 2ч. -Мн.: Выш. школа, 1989. Ч.1.
13. Гурский Е.И. Руководство к решению задач по высшей математике. В 2 ч. -Мн.: Выш. школа, 1990. Ч.2.
14. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч., ч.1. -М., Высш. школа, 1986, 1997, 1999
15. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч., Ч.2.-М., Высш. школа, 1986, 1997, 1999
16. Сухая Т.А., Бубнов В.Ф. Задачи по высшей математике. В 2 ч., ч.1-Мн.: Выш. школа, 1993.
17. Сухая Т.А., Бубнов В.Ф. Задачи по высшей математике. В 2 ч., ч.2.-Мн.: Выш. школа, 1993.
18. Индивидуальные задания по высшей математике (под ред. Рябушко А.П.). В 3 ч. -Мн.: Выш. школа, 2000.
19. Рябушко А.П. Индивидуальные задания по высшей математике. Мн.: Выш. школа, 2006
Контрольная работа №1
Задания 1-10. При условном делении экономики на три отрасли задана матрица коэффициентов прямых затрат А и вектор конечной продукции Y. Требуется:
1. Записать уравнение линейного межотраслевого баланса в координатной форме.
2. Найти плановые объемы выпуска валовой продукции отраслей. Систему линейных алгебраических уравнений решить методом Гаусса. Решение системы записать в неправильных дробях.
3. Выполнить проверку результата.
4. Записать приближенный ответ с точностью до сотых.
| 1. | А = 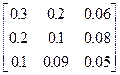 , Y = , Y = 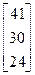 | 2. | А = 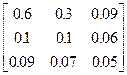 , Y = , Y = 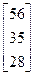 |
| 3. | А = 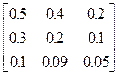 , Y = , Y = 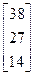 | 4. | А = 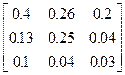 , Y = , Y = 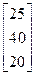 |
| 5. | А = 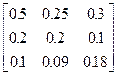 , Y = , Y = 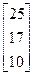 | 6. | А = 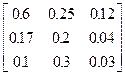 , Y = , Y = 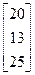 |
| 7. | А = 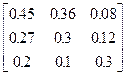 , Y = , Y = 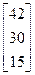 | 8. | А = 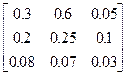 , Y = , Y = 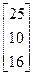 |
| 9. | А = 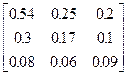 , Y = , Y = 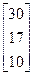 | 10. | А = 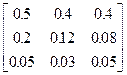 , Y = , Y = 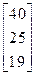 |
Задания 11-20.Даны векторы
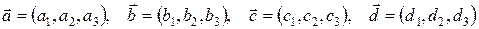 в некотором базисе.
в некотором базисе.
Показать, что векторы 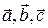 образуют базис и найти координаты вектора
образуют базис и найти координаты вектора 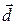 в этом базисе. Систему линейных уравнений решить по формулам Крамера.
в этом базисе. Систему линейных уравнений решить по формулам Крамера.
11. 
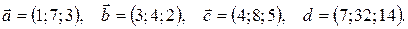
12. 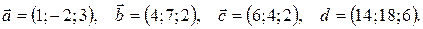
13. 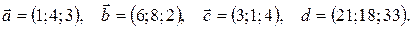
14. 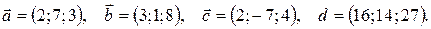
15. 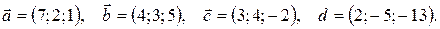
16. 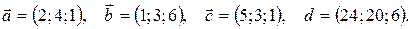
17. 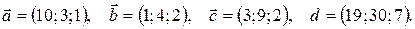
18. 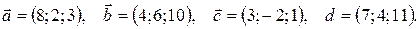
19. 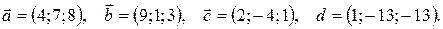
20. 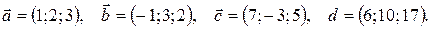
Задания 21-30. Даны координаты вершин пирамиды 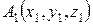 ,
, 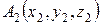 ,
, 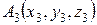 ,
, 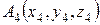 . Найти: 1) площадь грани
. Найти: 1) площадь грани 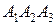 ;
;
2) объем пирамиды; 3) уравнения прямой 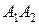 ; 4) уравнение плоскости
; 4) уравнение плоскости 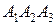 ; 5) уравнения высоты
; 5) уравнения высоты 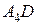 , опущенной из вершины
, опущенной из вершины 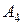 на грань
на грань 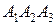 ; 6) длину высоты
; 6) длину высоты 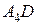 ; 7) координаты точки пересечения высоты
; 7) координаты точки пересечения высоты 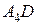 с плоскостью
с плоскостью 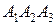 .
.
21. 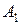 (3;1;4),
(3;1;4), 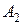 (-1;6;1),
(-1;6;1), 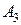 (-1;1;6),
(-1;1;6), 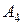 (0;4;-1).
(0;4;-1).
22. 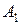 (3;-1;2),
(3;-1;2), 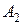 (-1;0;1),
(-1;0;1), 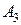 (1;7;3),
(1;7;3), 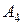 (8;5;8).
(8;5;8).
23. 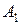 (3;5;4),
(3;5;4), 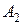 (5;8;3),
(5;8;3), 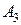 (1;2;-2),
(1;2;-2), 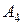 (-1;0;2).
(-1;0;2).
24. 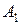 (2;4;3),
(2;4;3), 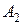 (1;1;5),
(1;1;5), 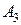 (4;9;3),
(4;9;3), 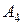 (3;6;7).
(3;6;7).
25. 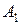 (9;5;5),
(9;5;5), 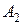 (-3;7;1),
(-3;7;1), 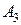 (5;7;8),
(5;7;8), 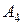 (6;9;2).
(6;9;2).
26. 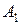 (0;7;1),
(0;7;1), 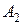 (2;-1;5),
(2;-1;5), 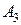 (1;6;3),
(1;6;3), 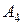 (3;-9;8).
(3;-9;8).
27. 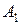 (5;5;4),
(5;5;4), 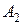 (1;-1;4),
(1;-1;4), 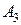 (3;5;1),
(3;5;1), 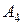 (5;8;-1).
(5;8;-1).
28. 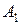 (6;1;1),
(6;1;1), 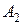 (4;6;6),
(4;6;6), 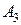 (4;2;0),
(4;2;0), 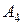 (1;2;6).
(1;2;6).
29. 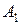 (7;5;3),
(7;5;3), 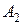 (9;4;4),
(9;4;4), 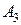 (4;5;7),
(4;5;7), 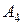 (7;9;6).
(7;9;6).
30. 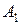 (6;8;2),
(6;8;2), 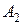 (5;4;7),
(5;4;7), 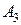 (2;4;7),
(2;4;7), 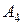 (7;3;7).
(7;3;7).
| 31. | На прямой 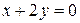 найти точку, равноудаленную от начала координат и от прямой найти точку, равноудаленную от начала координат и от прямой 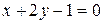 . Сделать чертеж. . Сделать чертеж. |
| 32. | Найти проекцию точки 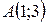 на прямую, проходящую через точку на прямую, проходящую через точку 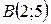 под углом 300 к оси Ох. Сделать чертеж. под углом 300 к оси Ох. Сделать чертеж. |
| 33. | Написать уравнение прямой, параллельной прямой 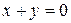 и отсекаю щей от координатных осей треугольник площадью 2 кв.ед. Сделать чертеж. и отсекаю щей от координатных осей треугольник площадью 2 кв.ед. Сделать чертеж. |
| 34. | Вычислить величину меньшего угла между прямыми 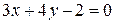 и и 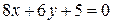 . Доказать, что точка . Доказать, что точка 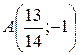 лежит на биссектрисе этого угла. Сделать чертеж. лежит на биссектрисе этого угла. Сделать чертеж. |
| 35. | Даны сторона прямоугольника 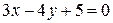 и две его вершины и две его вершины 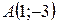 и и 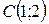 . Найти уравнения остальных сторон. Сделать чертеж. . Найти уравнения остальных сторон. Сделать чертеж. |
| 36. | Даны уравнение одной из сторон квадрата 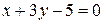 и точка и точка 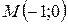 пересечения его диагоналей. Составить уравнения остальных трех сторон квадрата. Сделать чертеж. пересечения его диагоналей. Составить уравнения остальных трех сторон квадрата. Сделать чертеж. |
| 37. | Написать уравнение прямой, проходящей через точку пересечения прямых 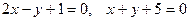 и пересекающей ось Ох под углом 300. Сделать чертеж. и пересекающей ось Ох под углом 300. Сделать чертеж. |
| 38. | Найти точку, симметричную точке 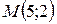 относительно прямой, проходящей через точки относительно прямой, проходящей через точки 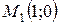 и и 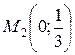 . Сделать чертеж. . Сделать чертеж. |
| 39. | Через начало координат проведена прямая на одинаковом расстоянии от точек 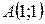 и и 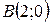 . Написать уравнение этой прямой. Сделать чертеж. . Написать уравнение этой прямой. Сделать чертеж. |
| 40. | Даны две вершины 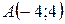 и и 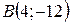 треугольника АВС и точка треугольника АВС и точка 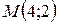 пересечения его высот. Найти вершину С. Сделать чертеж. пересечения его высот. Найти вершину С. Сделать чертеж. |
Задания 41-50.Вычислить пределы функций.
| 41. | |
1. 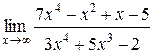 | 2. 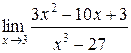 |
3. 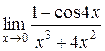 | 4. 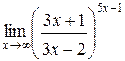 |
5. 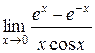 | |
| 42. | |
1. 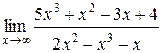 | 2. 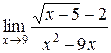 |
3. 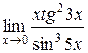 | 4. 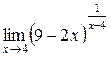 |
5. 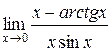 | |
| 43. | |
1. 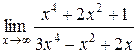 | 2. 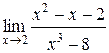 |
3. 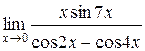 | 4. 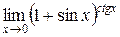 |
5. 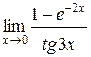 | |
| 44. | |
1. 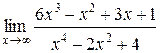 | 2. 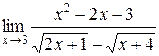 |
3. 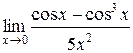 | 4. 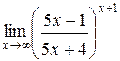 |
5. 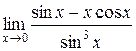 | |
| 45. | |
1. 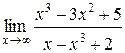 | 2. 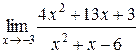 |
3. 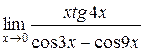 | 4. 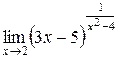 |
5. 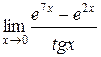 | |
| 46. | |
1. 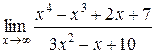 | 2. 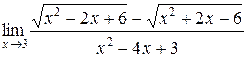 |
3. 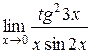 | 4. 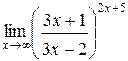 |
5. 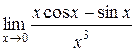 | |
| 47. | |
1. 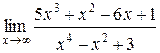 | 2. 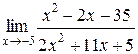 |
3. 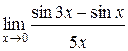 | 4. 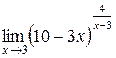 |
5. 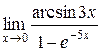 | |
| 48. | |
1. 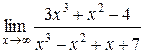 | 2. 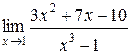 |
3. 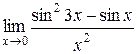 | 4. 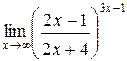 |
5. 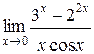 | |
| 49. | |
1. 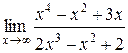 | 2. 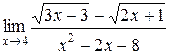 |
3. 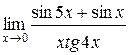 | 4. 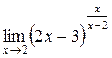 |
5. 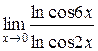 | |
| 50. | |
1. 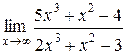 | 2. 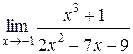 |
3. 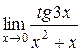 | 4. 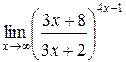 |
5. 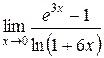 |
Задания 51-60. Найти производные 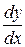 следующих функций.
следующих функций.
| 51. | ||
1. 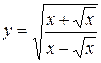 ; ; | 2. 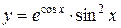 ; ; | 3. 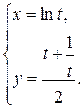 |
| 52. | ||
1. 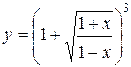 ; ; | 2. 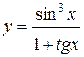 | 3. 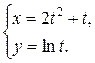 |
| 53. | ||
1. 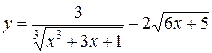 ; ; | 2. 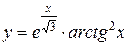 ; ; | 3. 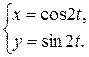 |
| 54. | ||
1. 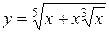 ; ; | 2. 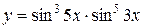 ; ; | 3. 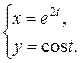 |
| 55. | ||
1. 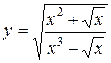 ; ; | 2. 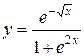 ; ; | 3. 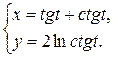 |
1. 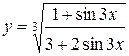 ; ; | 2. 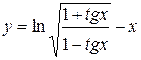 ; ; | 3. 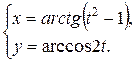 |
| 57. | ||
1. 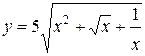 ; ; | 2. 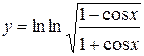 ; ; | 3. 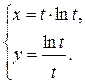 |
| 58. | ||
1. 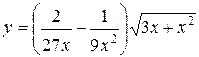 ; ; | 2. 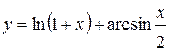 ; ; | 3. 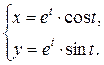 |
| 59. | ||
1. 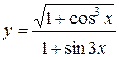 ; ; | 2. 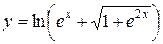 ; ; | 3. 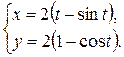 |
| 60. | ||
1. 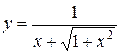 ; ; | 2. 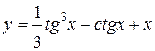 ; ; | 3. 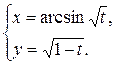 |
Задания 61-70. Исследовать методами дифференциального исчисления функцию 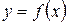 и, используя результаты исследования, построить ее график.
и, используя результаты исследования, построить ее график.
61. 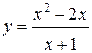 | 62. 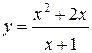 |
63. 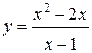 | 64. 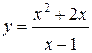 |
65. 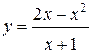 | 66. 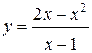 |
67. 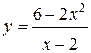 | 68. 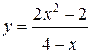 |
69. 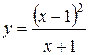 | 70. 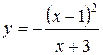 |
