Свободное движение системы

В общем случае реакция системы состоит из вынужденной и свободной составляющих y(t)=y_вын(t)+y_св(t), изображения которых имеют одинаковый знаменатель (характеристический полином систе­мы)

.

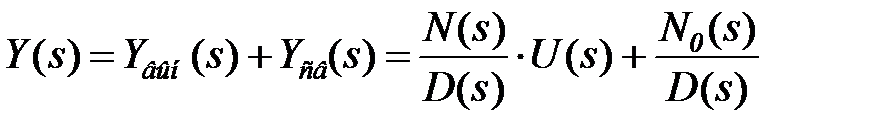Вынужденная составляющая y_вын(t) является реакцией системы на входное воздействие при нулевых начальных условиях y(0_) = 0. Свободная составляющая y_св(t) или переходный процесс автономной системы является решением однородного дифференциального урав­нения (без правой части) и определяется начальными условиями.

Используют два способа вычисления совокупного переходного процесса. В первом случае система обычно задается ОДУ, производят в соответствии со свойством дифференцирования преобразования Лапласа индивидуальное преобразование каждого члена дифференциального уравнения, вычисляются одновременно вынужденная и свободная составляющие.

По второму способу выполняют независимое вычисление вы­нужденной и/или свободной составляющих, при этом система обычно задана ПФ или структурной схемой. Для вычисления N₀(s) по D(s) ис­пользуется формула (схожая, но не равная вычислению производной)

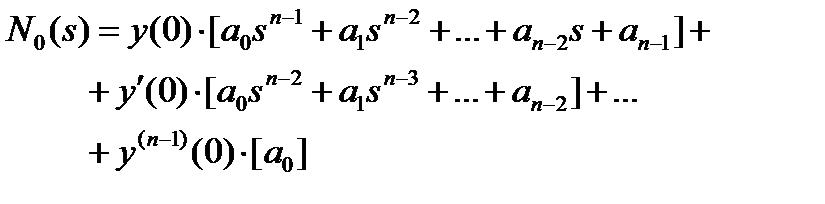
Если рассчитывается полное движение системы с учетом нену­левых начальных условий, запрещается производить сокращения в левой части ОДУ (в характеристическом полиноме D(s) системы). Вид характеристического полинома определяет свободную составляющую переходного процесса, т.е. реакцию на начальные условия.

Если начальные условия не заданы, то по умолчанию они счи­таются нулевыми. После получения результата стоит проверить, соответствует ли величина реакции на выходе при t = 0 заданным начальным условиям.

Пример 1. Для системы, заданной ОДУ , найти реакцию на начальные условия ; .

Преобразуем индивидуально каждый член ОДУ по Лапласу с учетом свойств дифференцирования оригинала при ненулевых начальных условиях

.

Группируем и переносим подобные члены, подставляем значения ;

,

.

Находим корни характеристического уравнения s₁ = -1, s₂ = -2 по известной формуле

записываем разложение на простые дроби, вычисляем вычеты в полюсах (смотри приложение Б), переходим к оригиналу по таблице А.1

,

.

При t = 0 начальное значение y(0) = 1 + 1 = 2, как и было задано.

Пример 2. Система задана ОДУ . Найти реакцию системы, если u(t) = δ(t), y(0) = 1, .

Прежде всего находим изображение входного воздействия по Лапласу из таблицы А.1. Вычисляем передаточную функцию и вынужденную составляющую переходного процесса

,

.

Определяем по характеристическому полиному числитель N₀(s) и свободную составляющую переходного процесса

,

.

Полное описание переходного процесса

.

Пример 3. Найти оригиналы по заданным изображениям, используя преобразование Лапласа:

По таблице преобразования Лапласа и свойствам преобразования Лапласа найдем

где I – единичная функция.

Для определения преобразования Лапласа от дроби F2(s) необходимо эту правильную рациональную дробь представить в виде суммы простейших дробей, которые определяются в соответствии с корнями характеристического уравнения и по которым преобразование Лапласа можно взять, используя таблицы преобразования; рассматриваемая дробь имеет три нулевых корня и пару комплексно-сопряженных корней, поэтому она разлагается на простейшие дроби следующим образом:

В результате разложения получена сумма простейших дробей, коэффициенты которых определяются методом неопределенных коэффициентов, для чего рассматривается равенство двух дробей. Две правильные рациональные дроби равны между собой, если равны их числители и знаменатели. Так как знаменатели равны, то, следовательно, необходимо приравнять друг к другу и числители. Приравняв в числителях коэффициенты при одинаковых степенях параметра s , получим систему алгебраических уравнений для определения неизвестных коэффициентов:

Решение системы дает следующие корни:

Таким образом, исходная дробь записывается в виде

В соответствии с таблицами преобразований Лапласа оригинал имеет вид

Пример 4.. С помощью преобразования Лапласа решить дифференциальное уравнение с заданными начальными условиями:

При решении уравнения с использованием преобразования Лапласа необходимо его преобразовать по Лапласу с учетом начальных условий:

Из последнего выражения определяется y(s) , которое и является решением уравнения, но оно записано в терминах преобразования Лапласа. Для получения решения уравнения во временной области полученная дробь разлагается на простейшие дроби, от которых в последствии по таблицам необходимо взять обратное преобразование Лапласа. В результате разложения получаем следующее выражение:

Приравнивая коэффициенты при одинаковых степенях s в числителе, записываем систему алгебраических уравнений для определения неизвестных коэффициентов

Решение системы:

Таким образом, дробь разложена на следующие простейшие дроби:

Взяв обратное преобразование Лапласа от последнего выражения, получим

Функция y(t) является решением дифференциального уравнения.

Пример 5. По известной кривой разгона и весовой функции линейного элемента найти:

1. реакцию на входной сигнал x(t) ;

2. весовую функцию или кривую разгона соответственно;

3. передаточную функцию элемента.

Задано: кривая разгона – h(t) = 2t ; весовая функция – ω(t) = 1− te^−t ; входной сигнал – x(t) =1− e^−t sin t .

1) Реакция элемента на входной сигнал определяется по интегралу Дюамеля, который может быть записан через кривую разгона или через весовую функцию.

Если известна кривая разгона, то интеграл Дюамеля записывается следующим образом:

следовательно,

Если известна весовая функция, то интеграл Дюамеля имеет вид

,

и тогда выходной сигнал в данной задаче будет записан как

2) Между кривой разгона и весовой функцией существует взаимная связь. Если известна кривая разгона, то весовая функция определяется как ω(t) = h′(t), т.е. ω(t) = (2t)′ = 2 .

Если же известна весовая функция, то кривая разгона

,

следовательно, в нашем случае

3) Передаточная функция, которая представляет собой отношение преобразованного по Лапласу выходного сигнала к преобразованному по Лапласу входному сигналу при нулевых начальных условиях, может быть определена как через кривую разгона, так и через весовую функцию:

Для нашей задачи: