Случай, когда пи-теорема дает вид зависимости с точностью до множителя

Формулировка

Для простоты ниже приводится формулировка для положительных величин .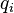

Предположим, что имеется зависимость между 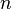физическими величинами , , , :

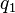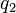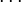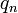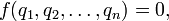
вид которой не меняется при изменении масштабов единиц в выбранном классе систем единиц (например, если используется класс систем единиц LMT, то вид функции 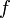не меняется при любых изменениях эталонов длины, времени и массы, скажем при переходе от измерений в килограммах, метрах и секундах к измерениям в фунтах, дюймах и часах).

Выберем среди аргументов функции наибольшую совокупность величин с независимыми размерностями (такой выбор можно, вообще говоря, производить различными способами). Тогда если число величин с независимыми размерностями обозначено 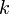и они занумерованы индексами 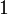, , 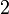, 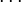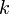(в противном случае их можно перенумеровать), то исходная зависимость 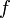эквивалентна зависимости между 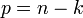безразмерными величинами , , , :

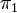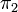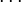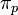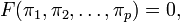
где 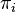— безразмерные комбинации, полученные из оставшихся исходных величин 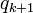, , 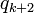, 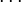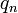делением на выбранные величины в соответствующих степенях:

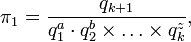
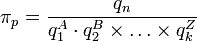
(безразмерные комбинации всегда существуют потому, что 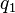, , 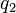, 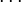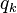— совокупность размерно-независимых величин наибольшего размера, и при добавлении к ним ещё одной величины получается совокупность с зависимыми размерностями).

Доказательство

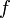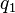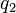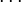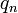Доказательство пи-теоремы очень простое. Исходную зависимость между , , , можно рассматривать как некоторую зависимость между 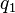, , 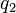, 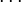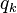и , , , :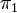

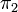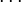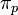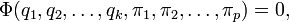
причем вид функции 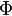также не меняется при изменении масштабов единиц. Остается заметить, что в силу размерной независимости величин 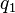, , 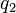, 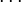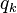всегда можно выбрать такой масштаб единиц, что эти величины станут равными единице, в то время как 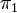, , 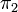, , 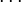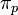будучи безразмерными комбинациями, своих значений не изменят, поэтому при так выбранном масштабе единиц, а значит, в силу инвариантности, и в любой системе единиц, функция 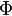фактически зависит только от :

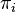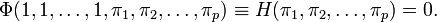
Частные случаи

]Применение к уравнению, разрешенному относительно одной величины

Часто используется вариант пи-теоремы для функциональной зависимости одной физической величины 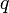от нескольких других , , , :

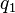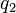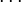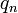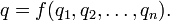
В этом случае пи-теорема утверждает, что зависимость эквивалентна связи

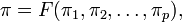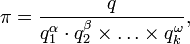где а 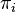определяются так же, как и выше.

Случай, когда пи-теорема дает вид зависимости с точностью до множителя

В одном важном частном случае, когда в зависимости

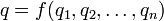
все аргументы имеют независимые размерности, применение пи-теоремы дает

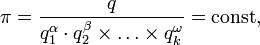
то есть вид функциональной зависимости определяется с точностью до константы. Значение константы методами теории размерностей не определяется, и для ее нахождения нужно использовать экспериментальные или другие теоретические методы.

Замечания о применении пи-теоремы

Выбор аргументов с независимыми размерностями, вообще говоря, можно делать различными способами, в результате чего при применении пи-теоремы формально могут получаться разные выражения. Однако на самом деле получающиеся результаты эквивалентны, и из одной формы записи можно получить другую путем перехода к комбинациям безразмерных параметров.

В формулировке пи-теоремы требование инвариантности зависимости является важным. Если, например, при работе в Международной системе единиц (СИ) в эксперименте была получена зависимость пути , пройденного падающим телом, от времени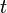

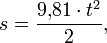
то в таком виде она не удовлетворяет условиям пи-теоремы.