При несимметричном напряжении

Расчет режима симметричной трехфазной нагрузки

при несимметричном напряжении

Пусть к симметричному трехфазному приемнику, например электродви­гателю, при­ложена несимметричная система напряжений U_A, U_B, U_C. Для по­лучения общих закономер­ностей введем в схему нулевой провод с сопротивле­нием Z_N. Схема цепи примет вид (рис. 108):

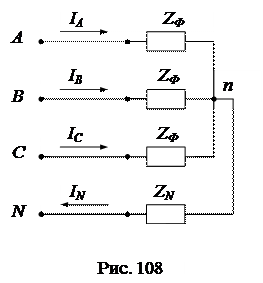Разложим несимметричную систему напряжений U_A, U_B, U_C на симмет­ричные состав­ляющие прямой, обратной и нулевой последовательностей:

,

,

.

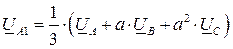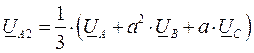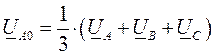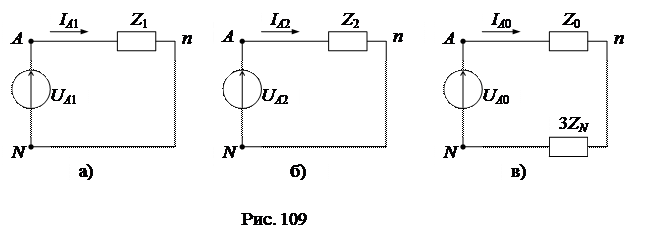
Применим к расчету схемы метод наложения и выполним расчет токов отдельно для каждой симметричной составляющей напряжения. Так как для каждой из симметричных со­ставляющих трехфазная схема генератор-приемник полностью симметрична, то расчет ре­жима можно выполнять только для одной фазы А, соответственно трехфазную схему следует заменить тремя однофаз­ными отдельно для каждой составляющей (рис. 109а, б, в). В симмет­ричном режиме для прямой и обратной последовательностей ток в нулевом проводе равен нулю и, следовательно, напряжение 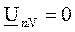. Это означает, что сопро­тивление в нейтраль­ном проводе Z_N не оказывает влияния на фазные токи и не должно включаться в схемы для этих последовательностей (рис. 109а, б). Токи нулевой последовательности во всех фазах сов­падают и могут замкнуться только через нулевой провод: I_N = I_A0 + I_B0 + I_C0 = 3I_A0. По 2-му закону Кирх­гофа для нулевой последовательности (рис. 3) получим:

U_A0 = I_A0Z₀ + I_N×Z_N = I_A0(Z₀ + 3Z_N)

Согласно полученному уравнению схема замещения для нулевой после­довательно­сти получит вид (рис. 109в), в которой последовательно с сопротив­лением фазы Z₀ включается утроенное сопротивление нейтрали 3Z_N.

В схемах для отдельных симметричных составляющих (рис. 4а, б, в) обозначены Z₁, Z₂, Z₀ - комплексные сопротивления фазы приемника для токов соответственно прямой, об­ратной и нулевой последовательностей. Для прием­ников с вращающимся магнитным полем эти сопротивления существенно от­личаются.

По закону Ома в каждой из схем рис. 109а, б, в производится расчет токов прямой, об­ратной и нулевой последовательностей:

; ; .

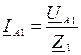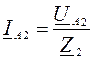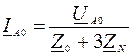Действительные токи в исходной схеме (рис. 108) определяются по ме­тоду наложения, как векторные суммы токов прямой, обратной и нулевой по­следовательностей:

I_A = I_A1 + I_A2 + I_A0 ,

I_B = I_B1 + I_B2 + I_B0 = a²×I_A1 +a×I_A2 + I_A0 ,

I_C = I_C1 + I_C2 + I_C0 =a×I_A1 + a²×I_A2 + I_A0 .

Комплексные сопротивления фаз статичных трехфазных приемников (ос­ветительная нагрузка, нагревательные приборы и др.) не зависят от вида после­довательности, для таких приемников 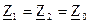. Расчет токов таких приемни­ков может выполняться обычными методами. Для трехфазных приемников, в которых существует вращающееся магнитное поле (электродвигатели, генера­торы), сопротивления фаз для токов разных последовательностей существенно отличаются ( 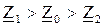). Расчет токов таких приемников при несимметрич­ном напряжении должен производиться исключительно методом симметрич­ных составляющих.