Сети с радиальной топологией
Билет 15.
MS Excel, функция МОПРЕД, решение системы линейных уравнений с двумя переменными, пример.
A)Вызываем «Мастер функций» → Категория «Математические» → Функция МОПРЕД
A1.1 * B1.2 * C1.3 = …n
A2.1 * B2.2 * C2.3 = …n
A3.1 * B3.2 * C3.3 = …n
Далее МОПРЕД и выделяем:
A1.1 * B1.2 * C1.3
A2.1 * B2.2 * C2.3
A3.1 * B3.2 * C3.3 = в отдельный столбец получаем матричный определитель.
B)Вот пример системы линейных уравнений:
3x + 4y = 8
4x + 8y = 1
Решение состоит в нахождении таких значений х и у, которые удовлетворяют обоим уравнениям. Эта система уравнений имеет одно решение:
x = 7,5
y = -3,625
Количество переменных в системе уравнений должно быть равно количеству уравнений. Предыдущий пример использует два уравнения с двумя переменными. Три уравнения требуются для того, чтобы найти значения трех переменных (х,у и z). Общие действия по решению систем уравнений следующие (рис. 128.1).
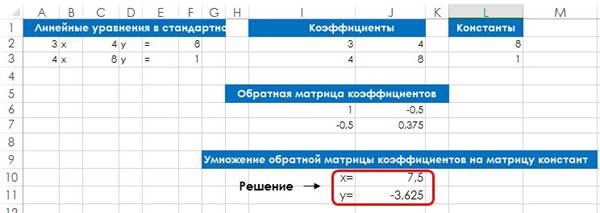
Рис. 128.1. Использование формулы для решения системы из двух уравнений.
- Выразите уравнения в стандартной форме. Если это необходимо, используйте основы алгебры и перепишите уравнение так, чтобы все переменные отображались по левую сторону от знака равенства. Следующие два уравнения идентичны, но второе приведено в стандартном виде:
3x - 8 = -4y
3x + 4y = 8. - Разместите коэффициенты в диапазоне ячеек размером n x n, где n представляет собой количество уравнений. На рис. 128.1 коэффициенты находятся в диапазоне I2:J3.
- Разместите константы (числа с правой стороны от знака равенства) в вертикальном диапазоне ячеек. На рис. 128.1 константы находятся в диапазоне L2:L3.
- Используйте массив формул для расчета обратной матрицы коэффициентов. На рис. 128.1 следующая формула массива введена в диапазон I6:J7 (не забудьте нажать Ctrl+Shift+Enter, чтобы ввести формулу массива): =МОБР(I2:J3).
- Используйте формулу массива для умножения обратной матрицы коэффициентов на матрицу констант. На рис. 128.1 следующая формула массива введена в диапазон J10:JJ11, который содержит решение (x = 7,5 и у = -3,625): =МУМНОЖ(I6:J7;L2:L3). На рис. 128.2 показан лист, настроенный для решения системы из трех уравнений.
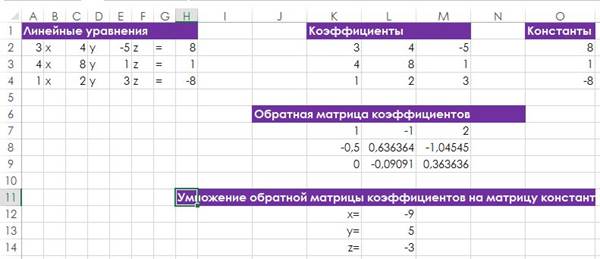
Рис. 128.2. В Excel можно решить систему из трех уравнений, применив нужные формулы.
Сети с радиальной топологией.
Топология "звезда" (радиальная, звездообразная) отличается тем, что все компьютеры подключаются к одному центральному (серверу). Для этого в центре сети содержится узел коммутации (коммутирующее устройство), к которому отдельным кабелем подключаются все компьютеры сети. Такой узел называется концентратором (hub).
Сигналы от передающего компьютера поступают через концентратор ко всем другим компьютерам.
Концентраторы делятся на активные и пассивные. Активные концентраторы передают сигналы так же, как репитеры (повторители), поэтому их называют многопортовыми повторителями. Обычно они имеют от 8 до 12 портов для подключения компьютеров. Активные концентраторы питаются от электрической сети.
К пассивным концентраторам относятся монтажные или коммутирующие панели, которые просто пропускают через себя сигнал, не усиливая и не восстанавливая его. Пассивным концентраторам не требуется питание от электрической сети.
Основное преимущество топологии "звезда" – высокая надежность. Выход из строя одного или нескольких компьютеров не приводит к потере работоспособности остальной части сети. Обрыв кабеля в одном месте приводит к отключению от сети только одного компьютера. Только неисправность концентратора приводит к полной потере работоспособности сети. Недостатком этой топологии является необходимость в дополнительном расходе кабеля и установке концентратора.
