Ороткі теоретичні відомості. Точність математичної моделі – її властивість, яка відбиває ступінь збігу передбачених з її допомогою значень характеристик об’єкта з дійсним значенням цих

Точність математичної моделі – її властивість, яка відбиває ступінь збігу передбачених з її допомогою значень характеристик об’єкта з дійсним значенням цих характеристик. За дійсне значення характеристик об’єкта звичайно приймають експериментально отримані значення.

Точність характеризується похибкою і є величиною, оберненою до неї. Похибка – це відхилення модельного значення від дійсного. У залежності від призначення моделі розглядають похибки абсолютні, відносні і зведені; максимальні, середні, середні квадратичні .

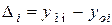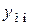- абсолютна похибка , де – модельне значення, отримане за результатами ідентифікації моделі, 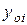- дійсне (експериментальне) значення;

- середня похибка 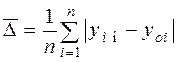, (2.1)

- середня квадратична похибка 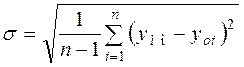(2.2)

- відносна похибка 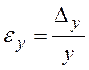; (2.3)

- зведена похибка 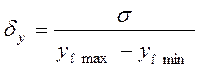, (2.4)

де 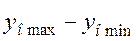- діапазон значень результатів;

- максимальна похибка 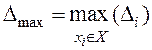. (2.5)

Похибки моделювання також класифікують за джерелами походження: методичні, обчислювальні, похибки від невизначеності початкових даних та ін.

Методичні похибки можуть бути викликані нехтуванням певними впливовими факторами, помилками у виборі виду функціональної залежності, невідповідністю способу отримання результату моделювання особливостям моделі, неправильним вибором типу моделі тощо.

Обчислювальні похибки викликані особливостями алгоритму отримання результату. При великій кількості послідовних обчислень похибка накопичується і може досягати значної величини. Такі ситуації виникають при розв’язанні диференціальних рівнянь, особливо у частинних похідних, та інших задачах.

Похибки від невизначеності початкових даних відіграють значну роль при використанні алгоритмів, які мають низьку стійкість. Так наприклад, при обчисленні похідної різницевим методом похибка результату може значно перевищувати похибки початкових даних.

Якщо визначені окремі похибки, то за умови їх незалежності загальна середня квадратична похибка підраховується за формулою

Побудова моделі складається з двох етапів: визначення узагальненої моделі всіх об’єктів заданого класу та визначення її характеристик для конкретного об‘єкта на основі різноманітної інформації. Останній етап називається ідентифікацією, тобто встановленням взаємно-однозначної відповідності між об’єктом і його моделлю.

Задача ідентифікації формулюється таким чином:

- за результатами спостережень за вхідними і вихідними змінними системи побудувати оптимальну в деякому сенсі її модель. При цьому система знаходиться в нормальному режимі функціонування (тобто, в середовищі випадкових впливів і завад).

Пасивним називається той експеримент, який проводиться шляхом спостереження змін стану об’єкта під дією зовнішніх впливів в процесі його нормального функціонування. Активний експеримент передбачає генерування діючих на об’єкт тестових сигналів потрібної форми, що скорочує його тривалість і спрощує наступне визначення параметрів моделі.

Задача ідентифікації статичної характеристики об’єкта на основі експериментальних даних є задачею її апроксимації (наближення) деякою аналітичною функцією. Найпоширенішою є апроксимація за методом найменших квадратів (МНК). Апроксимація здійснюється у два етапи:

1. На основі аналізу розташування експериментальних точок на графіку евристично визначається вигляд апроксимуючої функції.

2. Знаходяться оптимальні параметри функції за критерієм мінімуму СКВ.

Критерій мінімума СКВ вимагає, щоб сума квадратів відхилень спостережених значень 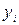від вибраної апроксимуючої функції 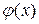була мінімальною:

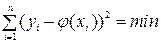(2.6)

Функція 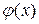зазвичай містить низку невідомих параметрів 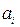, які потрібно вибрати згідно МНК:

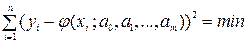. (2.7)

Для мінімізації виразу (5.2) його ліву частину по черзі диференціюємо по коефіцієнтах 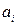і прирівнюємо до нуля. Отримуємо систему рівнянь з 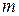невідомими, розв’язання якої дає можливість знайти невідомі числові значення параметрів 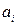і, тим самим, вираз функції :

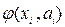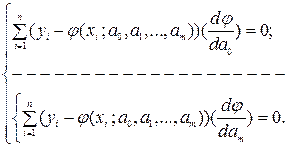(2.8)

Нехай, наприклад, задано набір експериментальних даних, що описують статичну характеристику ІВС

X
Y	1,2	2,1	5,6	9,8	16,2	28,1	37,3	54,1	68,2	91,1

Потрібно апроксимувати її поліномом.

Нанесемо експериментальні точки на графік (рис. 2.1).

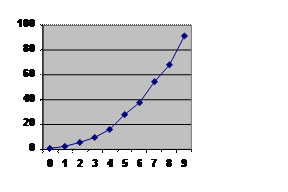Рисунок 2.1 – Статична характеристика ІВС

За виглядом графіка зробимо припущення, що експериментальні дані описуються квадратичною функцією

.

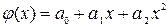Відповідно до методу найменших квадратів знайдемо коефіцієнти 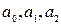, які забезпечують мінімальне СКВ:

.

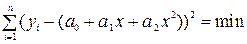Знаходимо частинні похідні лівої частини по коефіцієнтах 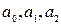і прирівнюємо їх до нуля:

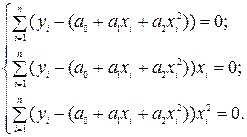(2.9)

Розкриваємо дужки і перетворюємо рівняння:

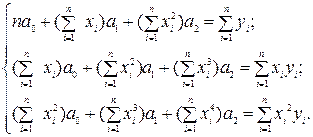(2.10)

Дана система є системою лінійних алгебраїчних рівнянь відносно невідомих 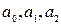і розв’язується одним із відомих чисельних методів. Найпростіше застосувати для цього вбудовану функцію Mathcad.

Завдання на роботу

1. В результаті пасивного експерименту у статичному режимі отримані такі значення вхідного і вихідного сигналів системи

X
Варіант	Y
	0,1	1,0	4,5	8,7	15,1	27,0	36,2	53,0	67,1	90,0
	-0,3	1,5	2,3	2,3	5,0	5,0	5,8	8,0	7,9	9,2
	5,3	5,0	3,1	2,6	0,9	-0,1	0,1	-1,5	-3,0	-3,5
	89,0	66,2	53,1	36,1	26,8	15,4	8,6	4,4	1,2	0,0
	9,7	7,9	8,1	5,6	5,1	4,7	2,3	2,5	1,3	-0,4
		1,3	2,6	3,1	3,8	4,2	4,4	4,5	4,6	4,8

Скласти алгоритм і програму на мові високого рівня для побудови аналітичної моделі системи у статичному режимі.

Виконати ідентифікацію статичної характеристики системи за допомогою складеної програми і в середовищі MathCad , вивести результати моделювання в табличному і графічному режимі.

Контрольні питання

1. Назвіть типи моделей за ознакою характеру процесів, що протікають в системі.

2. Дайте визначення статичним і динамічним моделям.

3. Назвіть основні етапи процесу моделювання.

4. Що називається точністю моделі?

5. Назвіть види похибок моделювання?

6. Які способи оцінки адекватності моделі вам відомі?

7. Які методи ідентифікації моделей ви знаєте?