Свойства универсального множества. Булева алгебра множеств. Число подмножеств

Булева алгебра множеств. Число подмножеств. Бинарные отношения. Отношения эквивалентности и частичного порядка. Отображения, взаимно-однозначные отображения. Мощность множества. Счетные множества и их свойства. Теорема Кантора о несчетности (0,1). Мощность континуума.

<F(U), ˅,˄ , ˉ > - сигнатура булевой алгебры.

А = <М, Q1,….Qn>-алгебра ( М-носитель алгебры, Qi-операции)

Пусть А-любое множество. Символом Р(А)={X/ X∈A} обозначается множество – степень (∑ всех возможных подмножеств множества А).

U- универсум. Универсальное множество —множество, содержащее все мыслимые объекты. Универсальное множество единственно.

Свойства универсального множества

· Любой объект, какова бы ни была его природа, является элементом универсального множества.

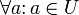
· В частности, само универсальное множество содержит себя в качестве одного из многих элементов.

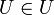
· Любое множество является подмножеством универсального множества.

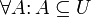
· В частности, само универсальное множество является своим подмножеством.

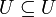
· Объединение универсального множества с любым множеством равно универсальному множеству.

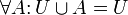
· В частности, объединение универсального множества с самим собой равно универсальному множеству.

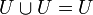
· Пересечение универсального множества с любым множеством равно последнему множеству.

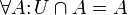
· В частности, пересечение универсального множества с самим собой равно универсальному множеству.

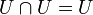
· Исключение универсального множества из любого множества равно пустому множеству.

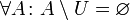
· В частности, исключение универсального множества из себя равно пустому множеству.

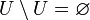
· Исключение любого множества из универсального множества равно дополнению этого множества.

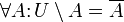
· Дополнение универсального множества есть пустое множество.

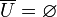
· Симметрическая разность универсального множества с любым множеством равна дополнению последнего множества.

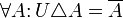
· В частности, симметрическая разность универсального множества с самим собой равна пустому множеству.

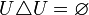
Элементы Булевой алгебры: а) числа b) переменные с) операции d) выражения e) функции f) законы.

Операции ˅,˄, ˉ - связаны между собой законами.

1. Закон коммутативности: A˅B=B˅A, A˄B=B˄A;

2. Закон ассоциативности: A˅(B˅C)=(A˅B)˅C, A˄(B˄C)=(A˄B)˄C;

3. Закон дистрибутивности: A˅(B˄C)=(A˅B) ˄(A˅C), A˄(B˅C)=(A˄B) ˅(A˄C);

4. Закон двойного отрицания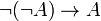

5.Законы де Моргана: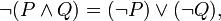

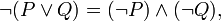
6. Законы поглощения: A˅ (A˄B)=A, A˄ (A˅B)=B;

Определение: Бинарным отношением между множествами X и Y называется любое подмножество ρ прямого произведения XхY.

Если X=Y => ρ ⊆XxY – бинарное отношение на Х

ρ ⊆XxY:

1) рефлексивное, если (х;х) ∈ρ (каждый элемент находится в отношении сам с собой).

2)симметричное, если (x,y) ∈ρ => (y,x)∈ρ;

3)транзитивное, если (x,y) ∈ρ, (y,z) ∈ρ => (x,z) ∈ρ;

4) антисимметричное, если (x,y) ∈ρ, (y,x) ∈ρ => x=y

Отношение ρ на Х,при условии, что выполнено 1, 2, 3 называется отношением эквивалентности:x ~ y;

Классом эквивалентности X(x) элемента x называется подмножество элементов, эквивалентных x. Из вышеприведённого определения немедленно следует, что, если y ∈X(x) то X(y)=X(x).

Множество всех классов эквивалентности обозначается .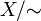

Определение: отношение ρ на Х,при условии, что выполнено 1, 4, 3 называется отношением частичного порядка;

Пусть P(U) – множество всех подмножеств множества U, отношение включения ⊆ на P(U) является отношением частичного порядка.

Определение: отношение ρ на Х,при условии, что выполнено 4, 3 называется отношением строгого частичного порядка;

Определение: ρ называется функцией из Х в У, или отображением, если каждому x∈X поставлено в соответствие единственное значение y изY:

f: X→Y∀x∈ X → ! f(x) ∈Y: y=f(x); При этом Х-область определения, У- область значения.

х- прообраз (аргумент)

у- образ (значение);

Определение: f называется отображением на (сюръекцией), если образ f(x) совпадает со всем множеством Y: ( f(x)=Y ⇔∀y∈Y ∃x∈ X: y=f(x))

Определение: f называется взаимооднозначным отображением (инъекцией) если для любого х1 ≠ х2 из Х,значения f(x1) ≠f(x2) (Образы различных элементов различны)

Определение : f называется взаимно-обратным отображением (биекцией), если оно инъективно и сюръективно.

Определение : число элементов множества А называется мощностью этого множества и обозначается |А|;

Определение: множества Ч и У называются равномощными(имеющими равную мощность), если между ними установлено взаимно-однозначное соответствие: ∃ f: X→Y ⇔|X|=|Y|;

Ex: f(n)=n², ∃ f: N→A ⇔|N|=|A|, N⊂A

А

N