1. Главная
  2. Математика
  3. Выводы и рекомендации по работе. По результатам 8 опытов ДФЭ 25-2 мы определили 10 значимых коэффициентов регрессии и получили адекватное уравнение регрессии

Выводы и рекомендации по работе. По результатам 8 опытов ДФЭ 25-2 мы определили 10 значимых коэффициентов регрессии и получили адекватное уравнение регрессии

По результатам 8 опытов ДФЭ 25-2 мы определили 10 значимых коэффициентов регрессии и получили адекватное уравнение регрессии. Полученная математическая зависимость, позволит определить параметры технологического процесса обеспечивающего высокие показатели качества дублированных текстильных материалов.

Оформить результаты работы в виде отчета по лабораторной работе в соответствии с требованиями (см. стр. 5).

Отчет по выполненной работе должен содержать:

1. Постановку задачи и цель работы.

2. Матрицу планирования эксперимента.

3. Результаты проверки воспроизводимости опытов.

4. Результаты расчетов коэффициентов регрессии и проверки их статистической значимости.

5. Результаты проверки адекватности полученной математической модели исходными экспериментальными данными.

6. Уравнение регрессии исследуемого объекта.

7. Генераторы плана. Контрасты плана.

8. Обобщающий контраст плана. Систему смешанности коэффициентов.

9. Выводы и предложения о ходе дальнейших исследований, составленные на основание анализа математической модели.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. В чем сущность ДФЭ, какие математические модели он позволяет исследовать?

2. Какую область описывает уравнение регрессии, полученное с помощью ДФЭ, и в каких границах его можно использовать?

3. Что такое взаимодействие факторов и сколько их может быть в ДЭФ?

4. В чем сущность и цели стандартизации масштаба факторов?

5. Как составляется и какими свойствами обладает матрица планирования ДФЭ?

6. Что такое генератор плана и как он выбирается?

7. Что такое контраст плана и обобщающий контраст?

8. Что такое смешанность оценок коэффициентов регрессии и как их найти?

9. Что такое разрешаю­щая способностью, как она обозначается?

10. В чем смысл «метода перевала» и когда его применяют?

11. Каков порядок постановки опытов при ДФЭ?

12. Как проверить воспроизводимость опытов?

13. Как рассчитать оценки коэффициентов регрессионного уравнения?

14. Как проверить статистическую значимость оценок коэффициентов регрессии?

15. Как проверить адекватность полученной математической модели?

16. Проведите сравнительный анализ ПФЭ и ДФЭ.

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

1. Сидняев Н. И. Теория планирования эксперимента и анализ статистических данных : учебное пособие / Н. И. Сидняев. – М. : ИД Юрайт, 2012. – 399 с.

2. Романов В. Н. Системный анализ для инженеров / В. Н. Романов. – СПб. : СЗГЗТУ, 2006. – 186 с.

3. Яворский В. А. Планирование научного эксперимента и обработка экспериментальных данных : учебное пособие / В. А. Яворский. – М. : МФТИ, 2006. – 24 с.

4. Рогов В. А. Методика и практика технических экспериментов : учебное пособие для вузов / В. А. Рогов, Г. Г. Позняк. – М. : Академия, 2005. – 283 с.

5. Джонсон И. Статистика и планирование эксперимента в технике и науке. Методы планирования эксперимента. Пер. с англ. / И. Джонсон, Ф. Лион. – М. : Мир, 1981. – 520с.

6. Современный эксперимент : подготовка, проведение, анализ результатов : учебник для вузов / В. Г. Блохин, О. П. Глудких, А. И. Гуров, Н. А. Ханин ; под ред. О. П. Глудких. – М. : Радио и связь, 1997.

7. Адлер Ю. П., Планирование эксперимента при поиске оптимальных условий / Ю. П. Адлер, Е. В. Маркова, Ю. В. Грановский. - М. : Наука, 1976. - 280 с.

8. Адлер Ю. П. Введение в планирование эксперимента / Ю. П. Адлер. - М. : Металлургия, 1969. - 157 с.

9. Асатурян В. И. Теория планирования эксперимента: Учеб. пособие для вузов. / В. И. Асатурян. - М. : Радио и связь, 1978. – 248 с.

10. Шустов Ю. С. Основы научных исследований свойств текстильных материалов / Ю. С. Шустов. – М. : Монография. – МГТУ им. А.Н. Косыгина, 2012. – 120 с.

11. Спирин Н. А. Методы планирования и обработки результатов инженерного эксперимента : конспект лекций / Н. А. Спирин, В. В. Лавров. – Екатеринбург : УГТУ-УПИ, 2004. – 257 с.

12. Рыков В. В. Математическая статистика и планирование эксперимента. Конспект лекций / В. В. Рыков, В. Ю. Иткин. – М. : , 2009. – 303 с.

13. ГореловаГ. В. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. – М. : Феникс, 2005. – 476 с.

14. Красовский Г.И. Планирование эксперимента / Красовский Г.И., Филаретов Г.Ф. – Мн. : Изд-во БГУ, 1982. – 302 с.

15. Налимов В.Н. Логические основания планирования эксперимента: учебник / В. Н.Налимов, Е .А. Шалыгина -2-е изд. – М. : Колос, 2001.

16. Планирование эксперимента – Режим доступа: URL: http://opds.sut.ru/electronic_manuals/pe/f053.htm

17. Программные пакеты (оболочки) для расчета статистических характеристик, планирования полного многофакторного эксперимента в среде MatLab и исследования поверхности отклика ПФЭ.

Приложение 1

Таблица значений критерия Кохрена Gтабл для уровня значимости 0,05:

f1 – число степеней свободы максимальной дисперсии - числитель;

f2 – число степеней свободы (число дисперсий) - знаменатель.

  f2 f1
0,998 0,975 0,939 0,906 0,877 0,853 0,833 0,816 0,801 0,734 0,660 0,500
0,967 0,871 0,798 0,746 0,707 0,677 0,653 0,633 0,617 0,547 0,475 0,333
0,906 0,768 0,684 0,629 0,589 0,560 0,536 0,518 0,502 0,437 0,372 0,250
0,841 0,684 0,598 0,544 0,506 0,478 0,456 0,439 0,424 0,364 0,307 0,200
0,781 0,616 0,532 0,480 0,445 0,418 0,398 0,382 0,368 0,314 0,261 0,167
0,727 0,561 0,480 0,431 0,397 0,373 0,354 0,338 0,326 0,276 0,228 0,143
0,680 0,516 0,438 0,391 0,360 0,336 0,318 0,304 0,293 0,246 0,202 0,125
0,638 0,478 0,403 0,358 0,329 0,307 0,290 0,277 0,266 0,223 0,182 0,111
0,602 0,445 0,373 0,331 0,303 0,282 0,267 0,254 0,244 0,203 0,166 0,100
0,471 0,335 0,276 0,242 0,220 0,203 0,191 0,182 0,174 0,143 0,114 0,067
0,389 0,270 0,220 0,192 0,174 0,160 0,150 0,142 0,136 0,111 0,088 0,050
0,293 0,198 0,159 0,138 0,124 0,116 0,106 0,101 0,096 0,077 0,060 0,033
0,174 0,113 0,090 0,076 0,068 0,063 0,058 0,055 0,052 0,041 0,032 0,017
0,100 0,063 0,050 0,042 0,037 0,034 0,031 0,030 0,028 0,022 0,016 0,008
                             

Приложение 2

Критические значения коэффициента Стьюдента (t-критерия) для различной доверительной вероятности p и числа степеней свободы f:

f p
0.80 0.90 0.95 0.98 0.99 0.995 0.998 0.999
3.0770 6.3130 12.7060 31.820 63.656 127.656 318.306 636.619
1.8850 2.9200 4.3020 6.964 9.924 14.089 22.327 31.599
1.6377 2.35340 3.182 4.540 5.840 7.458 10.214 12.924
1.5332 2.13180 2.776 3.746 4.604 5.597 7.173 8.610
1.4759 2.01500 2.570 3.649 4.0321 4.773 5.893 6.863
1.4390 1.943 2.4460 3.1420 3.7070 4.316 5.2070 5.958
1.4149 1.8946 2.3646 2.998 3.4995 4.2293 4.785 5.4079
1.3968 1.8596 2.3060 2.8965 3.3554 3.832 4.5008 5.0413
1.3830 1.8331 2.2622 2.8214 3.2498 3.6897 4.2968 4.780
1.3720 1.8125 2.2281 2.7638 3.1693 3.5814 4.1437 4.5869
1.363 1.795 2.201 2.718 3.105 3.496 4.024 4.437
1.3562 1.7823 2.1788 2.6810 3.0845 3.4284 3.929 4.178
1.3502 1.7709 2.1604 2.6503 3.1123 3.3725 3.852 4.220
1.3450 1.7613 2.1448 2.6245 2.976 3.3257 3.787 4.140
1.3406 1.7530 2.1314 2.6025 2.9467 3.2860 3.732 4.072
1.3360 1.7450 2.1190 2.5830 2.9200 3.2520 3.6860 4.0150
1.3334 1.7396 2.1098 2.5668 2.8982 3.2224 3.6458 3.965
Окончание таблицы приложения 2
f p
0.80 0.90 0.95 0.98 0.99 0.995 0.998 0.999
1.3304 1.7341 2.1009 2.5514 2.8784 3.1966 3.6105 3.9216
1.3277 1.7291 2.0930 2.5395 2.8609 3.1737 3.5794 3.8834
1.3253 1.7247 2.08600 2.5280 2.8453 3.1534 3.5518 3.8495
1.3230 1.7200 2.2.0790 2.5170 2.8310 3.1350 3.5270 3.8190
1.3212 1.7117 2.0739 2.5083 2.8188 3.1188 3.5050 3.7921
1.3195 1.7139 2.0687 2.4999 2.8073 3.1040 3.4850 3.7676
1.3178 1.7109 2.0639 2.4922 2.7969 3.0905 3.4668 3.7454
1.3163 1.7081 2.0595 2.4851 2.7874 3.0782 3.4502 3.7251
1.315 1.705 2.059 2.478 2.778 3.0660 3.4360 3.7060
1.3137 1.7033 2.0518 2.4727 2.7707 3.0565 3.4210 3.6896
1.3125 1.7011 2.0484 2.4671 2.7633 3.0469 3.4082 3.6739
1.3114 1.6991 2.0452 2.4620 2.7564 3.0360 3.3962 3.8494
1.3104 1.6973 2.0423 2.4573 2.7500 3.0298 3.3852 3.6460
1.3080 1.6930 2.0360 2.4480 2.7380 3.0140 3.3650 3.6210
1.3070 1.6909 2.0322 2.4411 2.7284 3.9520 3.3479 3.6007
1.3050 1.6883 2.0281 2.4345 2.7195 9.490 3.3326 3.5821
1.3042 1.6860 2.0244 2.4286 2.7116 3.9808 3.3190 3.5657
1.303 1.6839 2.0211 2.4233 2.7045 3.9712 3.3069 3.5510
1.320 1.682 2.018 2.418 2.6980 2.6930 3.2960 3.5370
1.301 1.6802 2.0154 2.4141 2.6923 3.9555 3.2861 3.5258
1.300 1.6767 2.0129 2.4102 2.6870 3.9488 3.2771 3.5150
1.299 1.6772 2.0106 2.4056 2.6822 3.9426 3.2689 3.5051
1.298 1.6759 2.0086 2.4033 2.6778 3.9370 3.2614 3.4060
1.2997 1.673 2.0040 2.3960 2.6680 2.9240 3.2560 3.4760
1.2958 1.6706 2.0003 2.3901 2.6603 3.9146 3.2317 3.4602
1.2947 1.6686 1.997 2.3851 2.6536 3.9060 3.2204 3.4466
1.2938 1.6689 1.9944 2.3808 2.6479 3.8987 3.2108 3.4350
1.2820 1.6640 1.9900 2.3730 2.6380 2.8870 3.1950 3.4160
1.2910 1.6620 1.9867 2.3885 2.6316 2.8779 3.1833 3.4019
1.2901 1.6602 1.9840 2.3642 2.6259 2.8707 3.1737 3.3905
1.2888 1.6577 1.9719 2.3578 2.6174 2.8598 3.1595 3.3735
1.2872 1.6551 1.9759 2.3515 2.6090 2.8482 3.1455 3.3566
1.2858 1.6525 1.9719 2.3451 2.6006 2.8385 3.1315 3.3398
1.2849 1.6510 1.9695 2.3414 2.5966 2.8222 3.1232 3.3299
1.2844 1.6499 1.9679 2.3388 2.5923 2.8279 3.1176 3.3233
1.2837 1.6487 1.9659 2.3357 2.5882 2.8227 3.1107 3.3150

Приложение 3

Плотность вероятности нормального распределения: 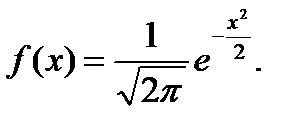Выводы и рекомендации по работе. По результатам 8 опытов ДФЭ 25-2 мы определили 10 значимых коэффициентов регрессии и получили адекватное уравнение регрессии - student2.ru

х
0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9   1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9   2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9   3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 0,3989   0,2420   0,0540   0,0044                                                              

Приложение 4

Значения критерия Фишера (F-критерия) для уровня значимости α=0,05

f1 - число степеней свободы большей дисперсии,

f2 - число степеней свободы меньшей дисперсии

  f1
f2
161.45 199.50 215.71 224.58 230.16 233.99 236.77 238.88 240.54 241.88 245.95
18.51 19.00 19.16 19.25 19.30 19.33 19.35 19.37 19.38 19.40 19.43
10.13 9.55 9.28 9.12 9.01 8.94 8.89 8.85 8.81 8.79 8.70
7.71 6.94 6.59 6.39 6.26 6.16 6.09 6.04 6.00 5.96 5.86
6.61 5.79 5.41 5.19 5.05 4.95 4.88 4.82 4.77 4.74 4.62
5.99 5.14 4.76 4.53 4.39 4.28 4.21 4.15 4.10 4.06 3.94
5.59 4.74 4.35 4.12 3.97 3.87 3.79 3.73 3.68 3.64 3.51
5.32 4.46 4.07 3.84 3.69 3.58 3.50 3.44 3.39 3.35 3.22
5.12 4.26 3.86 3.63 3.48 3.37 3.29 3.23 3.18 3.14 3.01
4.96 4.10 3.71 3.48 3.33 3.22 3.14 3.07 3.02 2.98 2.85
4.84 3.98 3.59 3.36 3.20 3.09 3.01 2.95 2.90 2.85 2.72
4.75 3.89 3.49 3.26 3.11 3.00 2.91 2.85 2.80 2.75 2.62
4.67 3.81 3.41 3.18 3.03 2.92 2.83 2.77 2.71 2.67 2.53
4.60 3.74 3.34 3.11 2.96 2.85 2.76 2.70 2.65 2.60 2.46
4.54 3.68 3.29 3.06 2.90 2.79 2.71 2.64 2.59 2.54 2.40
4.49 3.63 3.24 3.01 2.85 2.74 2.66 2.59 2.54 2.49 2.35
4.45 3.59 3.20 2.96 2.81 2.70 2.61 2.55 2.49 2.45 2.31
4.41 3.55 3.16 2.93 2.77 2.66 2.58 2.51 2.46 2.41 2.27
4.38 3.52 3.13 2.90 2.74 2.63 2.54 2.48 2.42 2.38 2.23
4.35 3.49 3.10 2.87 2.71 2.60 2.51 2.45 2.39 2.35 2.20

УЧЕБНОЕ ИЗДАНИЕ

Наши рекомендации

Уравнение регрессий и ломаная (эмпирическая регрессия). Ошибка уравнения регрессии. Значимость уравнения регрессии.

Проверка гипотезы о значимости коэффициентов регрессии и модели множественной регрессии в целом

Оценка уравнения регрессии и построение доверительных интервалов для коэффициентов регрессии

Выводы и рекомендации по работе. Должны содержать заключение о значимости коэффициентов регрессии, уравнение регрессии и заключение о его адекватности поверхности отклика исследуемого

Выводы и рекомендации по работе. Должны содержать заключение о значимости коэффициентов регрессии, уравнение регрессии и заключение о его адекватности поверхности отклика исследуемого

Уравнение регрессии, его смысл и назначение. Выбор типа математической функции при построении уравнения регрессии.

Теорема Гаусса-Маркова для множественной регрессии. Определение ковариационно – дисперсионной матрицы вектора коэффициентов регрессии.

Регрессионный анализ. Ошибки оценок коэффициентов регрессии. Проверка гипотез о значимости коэффициентов регрессии и уравнения регрессии в целом.

Проверка значимости уравнение и коэффициентов уравнения регрессии

Записать уравнение регрессии в общем виде, определить его параметры и дать интерпретацию коэффициента регрессии;