Системы управления запасами
Проблема управления запасами актуальна практически для любой производственной или торговой организации. Чрезмерная величина запасов связывает оборотные средства предприятия, что приводит к снижению ликвидности и другим неприятным последствиям. Недостаточная величина запасов может привести к остановке производства или потерям, связанным с упущенными клиентами. Управление запасами заключается в определении оптимальной для данного предприятия периодичности поставок сырья и материалов и в определении оптимальной величины поставок. Совокупность правил, по которым принимаются эти решения, называют системой управления запасами.
Чаще всего оптимизируются такие показатели работы склада, размеры и периодичность заказа на пополнение запасов, поддерживаемый уровень запасов.
Наиболее полно описаны в литературе и чаще встречаются на практике системы управления запасами с фиксированным размером заказа. В такой системе размер заказа на пополнение запасов является величиной постоянной, а очередная поставка товаров осуществляется при уменьшении наличных запасов до определенного критического уровня (так называемой точки заказа, или точки восстановления запаса). В процессе функционирования системы запас пополняется каждый раз на одну и ту же величину, но интервалы пополнения могут быть различными в зависимости от скорости расходования запаса.
В качестве функции цели в математических моделях управления запасами чаще всего используется функция затрат 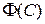 , связанных с заготовкой и содержанием запасов, а также с перебоями в снабжении потребителей (потери от дефицита).
, связанных с заготовкой и содержанием запасов, а также с перебоями в снабжении потребителей (потери от дефицита).
1. Расходы на хранение включают в себя расходы на содержание складского помещения (или плату за аренду), оплату труда складского персонала и амортизацию оборудования, потери от естественной убыли хранимых материалов. Эти издержки прямо пропорциональны величине поставки.
2. Расходы, входящие в стоимость поставки, включают расходы, связанные с оформлением заказа, заключением договоров и соглашений на поставку, почтовые, телеграфные, канцелярские и прочие управленческие расходы. Эти расходы не зависят от размера заказываемой партии.
3. Потери от дефицита трактуются как величина упущенной выгоды из-за неудовлетворенного спроса (из-за отсутствия на складе товаров в тот момент, когда покупатель был готов их купить).
Отметим, функция затрат 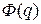 не обязательно должна включать в себя все виды издержек. Существуют модели управления запасами, в которых допускаются случаи дефицита, существуют и те, в которых дефицит не учитывается.
не обязательно должна включать в себя все виды издержек. Существуют модели управления запасами, в которых допускаются случаи дефицита, существуют и те, в которых дефицит не учитывается.
В настоящее время разработано множество различных видов моделей управления запасами: детерминированные (все параметры модели фиксированы), стохастические, статические, динамические (допускается изменение некоторых параметров во времени, например, изменение величины спроса).
Наиболее распространенными и простыми для понимания являются детерминированные модели управления запасами. Ниже рассмотрим одну из таких моделей [1].
Модель Уилсона.
Модель Уилсона позволяет определить оптимальную величину заказа товара, при которой издержки на оформление, доставку и хранение товара за некоторый период времени (чаще всего, за год) будут минимальными.
Допущения модели:
1) уровень запасов убывает с постоянной интенсивностью (уровень спроса постоянный);
2) выполнение заказа осуществляется мгновенно, т.е. время доставки равно нулю;
3) накладные расходы, связанные с размещением заказа и поставкой товара не зависят от объема партии и равны постоянной величине 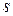 ;
;
4) стоимость хранения единицы товара за период времени постоянна.
Процесс восстановления уровня запасов показан на рисунке 6.
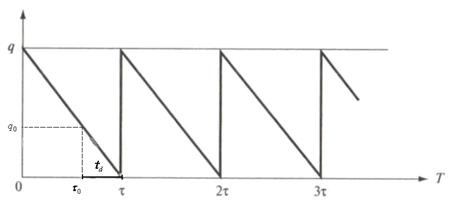
Рис. 6. Процесс изменения уровня запасов в модели Уилсона.
Введем обозначения: 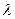 – спрос (интенсивность расходования запасов), за период времени T;
– спрос (интенсивность расходования запасов), за период времени T; 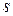 – расходы на оформление заказа;
– расходы на оформление заказа; 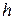 – стоимость хранения единицы товара за единицу времени;
– стоимость хранения единицы товара за единицу времени; 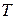 – интервал времени, для которого рассчитывается оптимальный объем заказа (время моделирования);
– интервал времени, для которого рассчитывается оптимальный объем заказа (время моделирования); 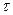 – период времени между поставками (длина цикла);
– период времени между поставками (длина цикла); 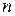 – общее число заказанных партий за период
– общее число заказанных партий за период 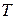 ;
; 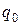 – точка заказа, то есть объем запасов на складе, при котором надо заказывать очередную партию;
– точка заказа, то есть объем запасов на складе, при котором надо заказывать очередную партию; 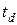 – время доставки;
– время доставки; 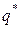 – оптимальный объем заказываемой партии;
– оптимальный объем заказываемой партии;
Предположим, что величина спроса за период 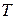 известна и равна
известна и равна 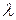 . Тогда общее число заказанных партий за весь период
. Тогда общее число заказанных партий за весь период 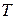 можно найти как
можно найти как
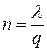 , (21)
, (21)
где 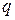 - размер заказываемой партии. С другой стороны, если известна длина цикла
- размер заказываемой партии. С другой стороны, если известна длина цикла 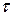 , то количество партий за период
, то количество партий за период 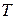 можно найти как
можно найти как
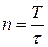 . (22)
. (22)
Средний уровень запасов за период времени продолжительность 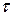 (дней) равен
(дней) равен 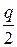 , тогда затраты на хранение этого количества запасов за период
, тогда затраты на хранение этого количества запасов за период 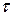 будут равны
будут равны 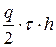 . Так как за период времени, равный
. Так как за период времени, равный 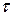 запасы пополняются один раз, то общие затраты на заказ и хранение одной партии будут равны
запасы пополняются один раз, то общие затраты на заказ и хранение одной партии будут равны 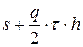 .
.
Тогда функция затрат за период времени 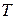 будет равна:
будет равна:
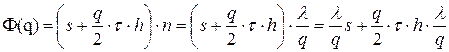 . (23)
. (23)
В формуле (23) заменим дробь 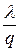 на
на 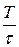 в силу (21) и (22), и получим:
в силу (21) и (22), и получим:
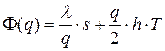 . (24)
. (24)
Выражение (24) - это функция затрат в модели управления запасами. Чтобы определить при каком значении 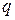 (размер партии) совокупные затраты будут минимальны, необходимо взфть производную по
(размер партии) совокупные затраты будут минимальны, необходимо взфть производную по 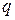 и приравнять ее к нулю:
и приравнять ее к нулю:
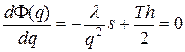
Оптимальный размер партии 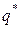 будет равен:
будет равен:
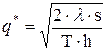 (25)
(25)
Используя соотношения (21) и (22) можно вывести формулы для 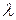 ,
, 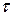 и
и 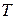 . Например, длительность цикла заказа равна
. Например, длительность цикла заказа равна
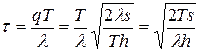 . (26)
. (26)
Точка заказа 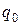 - это такой уровень запаса, при достижении которого делается новый заказ.
- это такой уровень запаса, при достижении которого делается новый заказ.
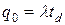 , (27)
, (27)
где 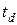 - время доставки заказа.
- время доставки заказа.
Замечание. В формуле (27) значения 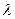 и
и 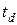 должны быть приведены к одному периоду времени. Если известен объем спроса за год, то время доставки тоже надо выразить в долях года. Или наоборот, если известен срок доставки в днях, то надо вычислить объем спроса за 1 день.
должны быть приведены к одному периоду времени. Если известен объем спроса за год, то время доставки тоже надо выразить в долях года. Или наоборот, если известен срок доставки в днях, то надо вычислить объем спроса за 1 день.
Модель Уилсона проста и удобна в использовании, но мало применима на практике, из-за жестких допущений, которые лежат в ее основе. Рассмотрим их подробнее.
На практике интенсивность спроса редко бывает постоянна. Величина спроса зависит от множества факторов, таких как сезонность, цена, наличие на рынке аналогичных товаров и т.д. В общем случае величину спроса можно рассматривать как случайную величину, которая теоретически может принять любое значение. Закон распределения спроса можно приближенно установить по данным за предшествующие периоды времени.
В модели Уилсона предполагается, что доставка заказа и пополнение запаса происходит мгновенно. В это, естественно, не так. Время доставки также зависит от множества факторов, таких как вид товара, объем поставки, условия перевозки, время года, загруженность транспорта и т.д. Время доставки также следует рассматривать как случайную величину со своим законом распределения.
И наконец, в модели Уилсона предполагается, что расходы, связанные с оформлением заказа и расходы на хранение единицы запаса постоянны. И это предположение не соответствует действительности. Расходы на оформление заказа могут меняться в зависимости от вида товара, удаленности поставщика, условий доставки груза. Затраты на хранение запасов зависят от величины этих запасов. От количества хранящегося на складе имущества зависит и количество складских работников, и режим охраны склада и затраты на электроэнергию и обогрев складских помещений.
Очевидно, что предпосылки, лежащие в основе модели Уилсона (и многих других моделей управления запасами) далеки от реальности. Если при управлении запасами использовать оценки, полученные при помощи детерминированной модели (оптимальный размер партии 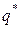 , длительность цикла
, длительность цикла 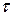 ), это может привести к существенным экономическим потерям.
), это может привести к существенным экономическим потерям.
Попробуем использовать метод имитации для определения приемлемых параметров работы склада.
