Метод включения-исключения
Пусть имеется множество элементов 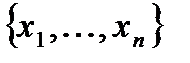 и пусть имеется множество свойств
и пусть имеется множество свойств 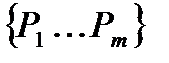 , которыми элементы
, которыми элементы 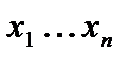 могут обладать или нет. Пусть
могут обладать или нет. Пусть  — число элементов, обладающих свойствами
— число элементов, обладающих свойствами 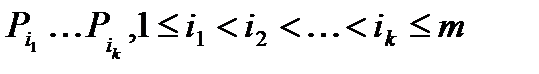 . Пусть
. Пусть 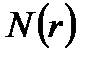 обозначаетчислоэлементов, обладающих ровно
обозначаетчислоэлементов, обладающих ровно 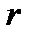 свойствами.
свойствами.
Теорема. 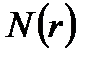 =
= 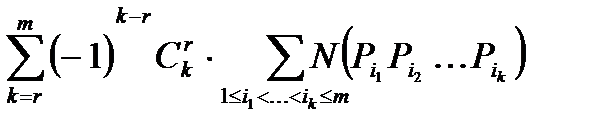
Доказательство.
1. Рассмотрим элемент 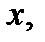 обладающий ровно
обладающий ровно 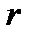 свойствами. Такой элемент войдет в
свойствами. Такой элемент войдет в 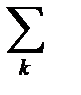 только при
только при 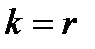 и в сумме
и в сумме 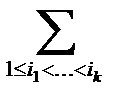 будетсчитаться единственный раз. Поэтому элементы, обладающиеровно
будетсчитаться единственный раз. Поэтому элементы, обладающиеровно 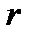 свойствами, будут входить в сумму по одному разу.
свойствами, будут входить в сумму по одному разу.
2. Рассмотрим элемент 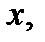 обладающий ровно
обладающий ровно 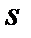 свойствами,
свойствами, 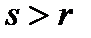 .Тогда в
.Тогда в 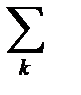 они будут входить при
они будут входить при 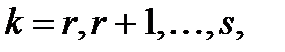 а в
а в 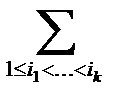 они войдут
они войдут 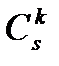 раз. Тогда общее число вхождений такого элемента
раз. Тогда общее число вхождений такого элемента 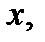 есть
есть
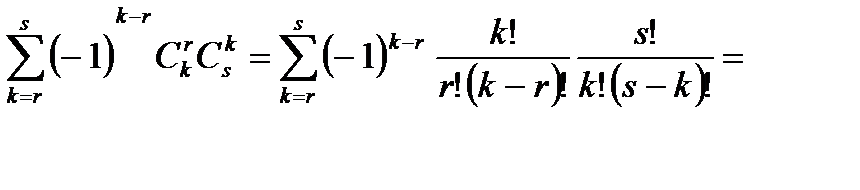
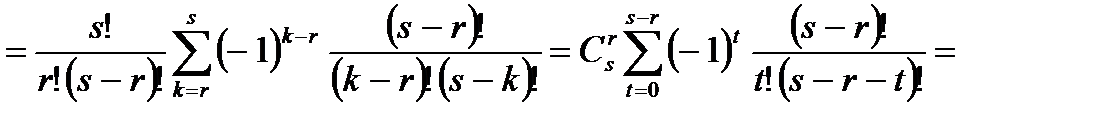
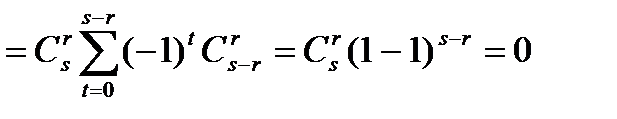
Таким образом, из 1 и 2 следует требуемое свойство.
Пример 1. Подсчитать число перестановок, оставляющих на месте ровно 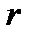 элементов.
элементов.
Решение. Вводим множество всех перестановок 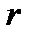 элементов
элементов 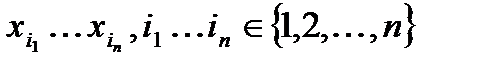 . Вводим n свойств
. Вводим n свойств 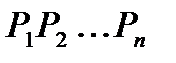 :
: 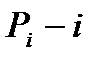 -тый элемент при перестановке
-тый элемент при перестановке 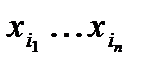 остается на месте. Тогда число перестановок, оставляющих на месте ровно
остается на месте. Тогда число перестановок, оставляющих на месте ровно 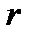 элементов, есть:
элементов, есть: 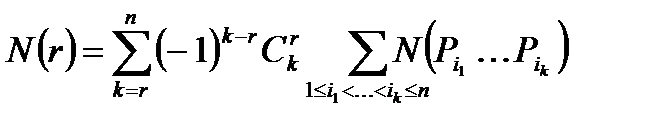
где N( 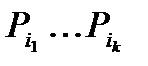 ) — число перестановок, оставляющих на месте
) — число перестановок, оставляющих на месте 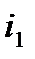 -ый,
-ый, 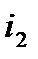 -ой,…,
-ой,…, 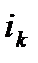 -ый элементы, и это число есть очевидно, (n-k)!, а число слагаемых в сумме
-ый элементы, и это число есть очевидно, (n-k)!, а число слагаемых в сумме 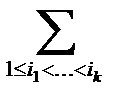 есть
есть 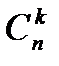 . Поэтому искомое число есть
. Поэтому искомое число есть
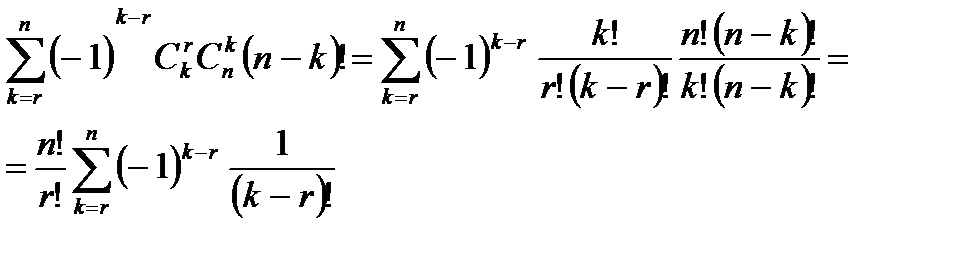
Здесь 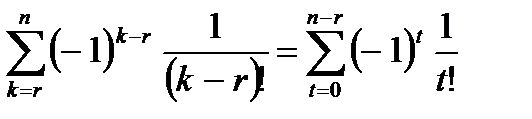
И при больших 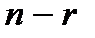 получим ассимтотическую формулу
получим ассимтотическую формулу 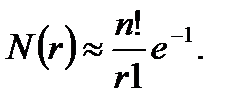
Пример 2. Найти число чисел взаимно простых с данным 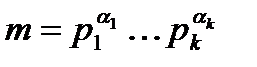 . Обозначим это число через
. Обозначим это число через 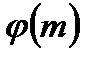 (так называемая функция Эйлера).
(так называемая функция Эйлера).
Решение. Введем множество натуральных чисел 1, 2,..., т и введем свойства 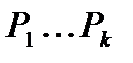 , где
, где 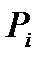 означает, что число делится на простое число
означает, что число делится на простое число 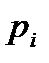 . Тогда числа взаимно простые с т есть числа, которые не обладают ни одним из свойств
. Тогда числа взаимно простые с т есть числа, которые не обладают ни одним из свойств 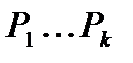 , т.е. обладают 0 свойствами, и поэтому искомое число есть
, т.е. обладают 0 свойствами, и поэтому искомое число есть
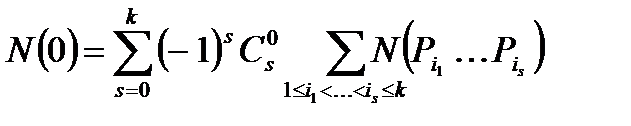
где 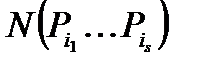 есть число чисел, делящихсяна
есть число чисел, делящихсяна 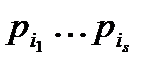 , и поэтому это числа, представленные в виде
, и поэтому это числа, представленные в виде 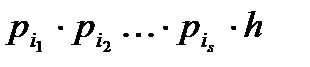
где множитель h изменяется 1,2, 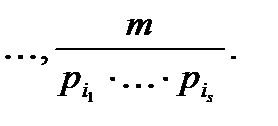 Поэтому
Поэтому 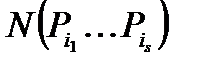 =
= 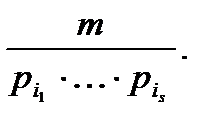
и тогда 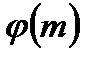 =
= 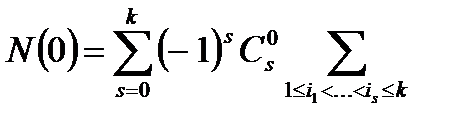
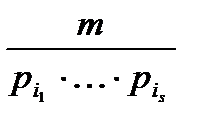 =
=
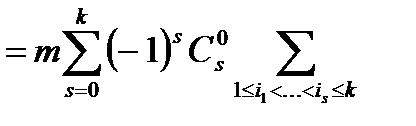
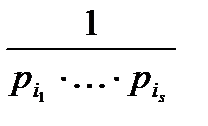
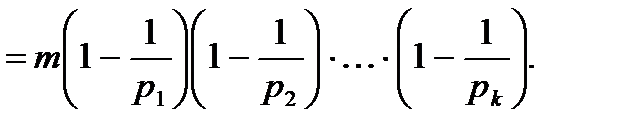
Пример 3. Найти число способов раскладки m различных шаров по n различным урнам, при которых ровно 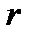 урн пусты.
урн пусты.
Решение. Введем множество различных раскладок m различных шаров по n различным урнам, т.е. упорядоченных наборов m элементов из множества {1,2,..., n} n-элементов с возможными повторениями. Введем свойства раскладок 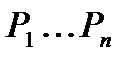 .
. 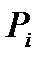 — i-ая урна пуста. Тогда искомое число есть
— i-ая урна пуста. Тогда искомое число есть 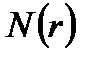 — ровно
— ровно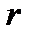 урн пусты.
урн пусты. 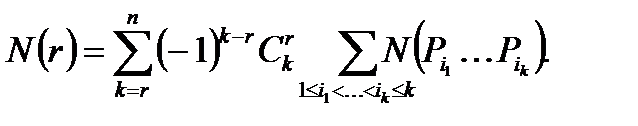
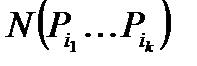 — число раскладок, при которых
— число раскладок, при которых 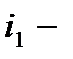 ая,
ая, 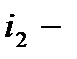 ая,
ая, 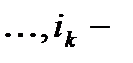 ая урны пусты и это число, как нетрудно видеть, есть
ая урны пусты и это число, как нетрудно видеть, есть 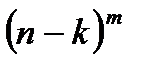 .Поэтому
.Поэтому 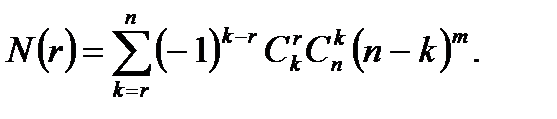
Упражнения.
1. Имеется колода карт четырех мастей по n карт каждой масти. Берут 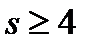 карт. Найти число комбинаций, в которых имеются все масти.
карт. Найти число комбинаций, в которых имеются все масти.
2. Бросают 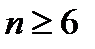 различных игральных кубиков.Найти число комбинаций, когда имеются все цифры.
различных игральных кубиков.Найти число комбинаций, когда имеются все цифры.
3. Найти число квадратных двоичных матриц размера n 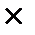 n, в каждой строке которых содержится хотя бы один ноль.
n, в каждой строке которых содержится хотя бы один ноль.
4. Найти число двоичных матриц размера 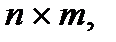 n в строках, которых содержатся все двоичные слова длины m.
n в строках, которых содержатся все двоичные слова длины m.
5. Составляют n-значные числа из цифр 1,2,3,4. Найти число чисел, в
которых имеются все цифры.
